INCOMING TRANSMISSION

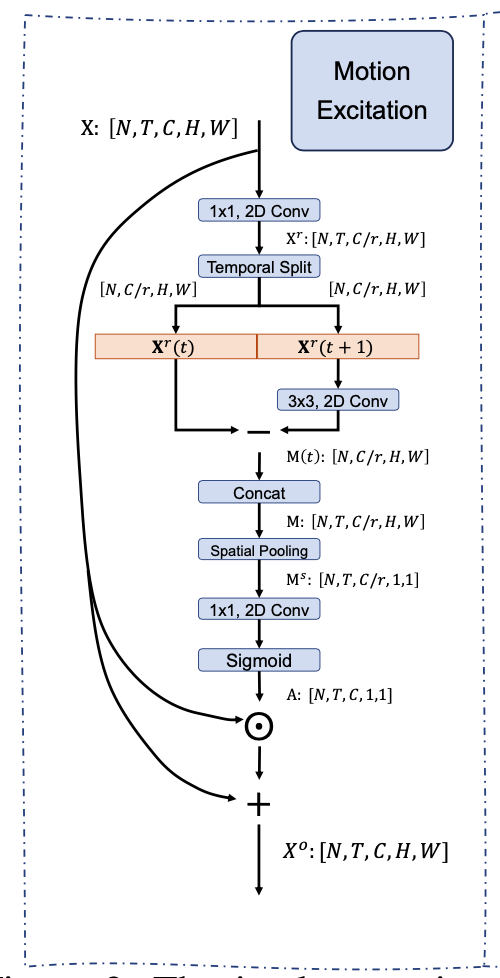
Motivation Motion feature 学习过程中存在的问题： 利用 optical flow 存储和计算的开销太大 现阶段的网络设计，spatiotemporal 建模 和Motion feature 建模分离 比如STM 直接 Add spatio temporal feature 和 motion encoding feature TEA 的 ME 则利用了 Motion feature 做 channeI attention 过去的建模都 focus 在 framelevel motion，更好的建模方式 featurelevel motion 长时建模存在的问题： 单帧过backbone，最后的feature 进行 temporal max/average poolin...

研究动机 目前 3Dbased 的方法在大规模的 scenebased 的数据集(如kinetics)上相对于2D的方法取得了更好的效果，但是3Dbased也存在一些明显的问题： 3Dbased 的网络参数量大，计算开销大，训练的 scheduler 更长，inference latency 明显慢于 2Dbased 的方法。 3D卷积其实并不能很好得学到时序上信息的变化，而且3D卷积学出来的时序Kernel的weight的分布基本一致，更多的还是对时序上的信息做一种 smooth aggregation。这一点在之前的工作TANet 中有比较详细的讨论。也基于此，3Dbased 的网络在SomethingSomething这种对时序信息比较敏感的video数据集上并不能取得很好的效果( 得...

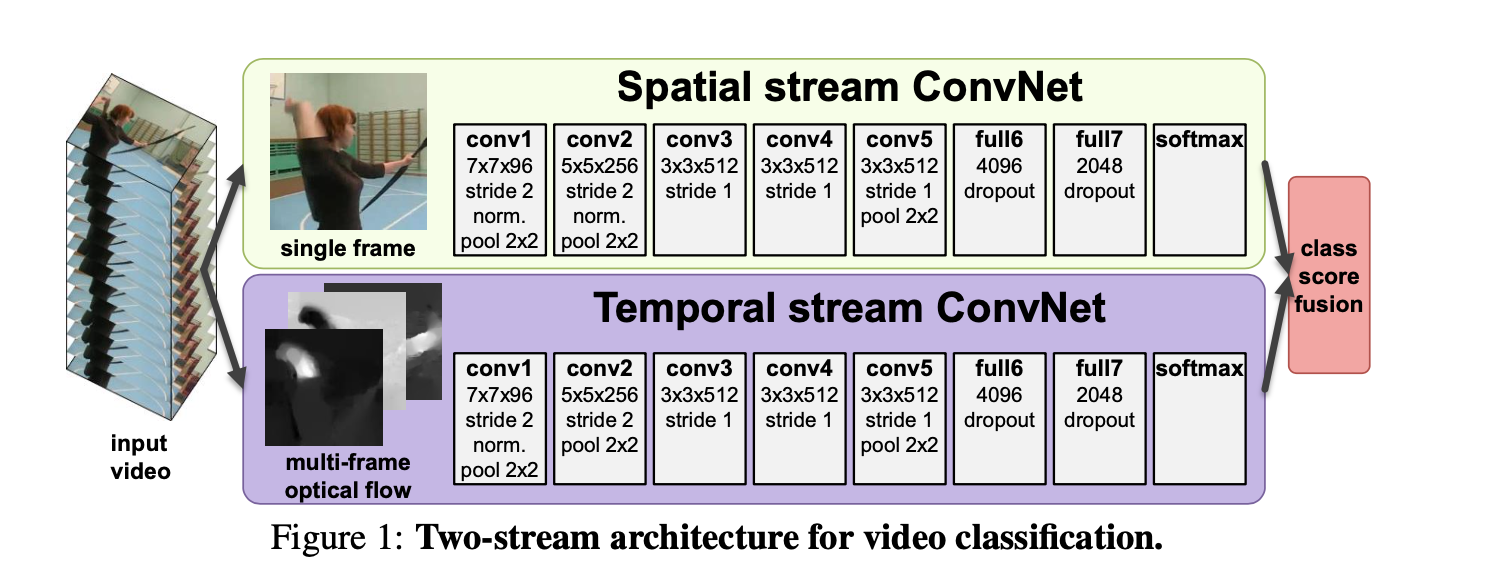
Classification，Detection Classification：给定预先裁剪好的视频片段，预测其所属的行为类别 Detection：视频是未经过裁剪的，需要先进行人的检测where和行为定位（分析行为的始末时间）when，再进行行为的分类what。 通常所说的行为识别更偏向于对时域预先分割好的序列进行行为动作的分类，即 Trimmed Video Action Classification。 TwoStream Twostream convolutional networks 简介 TwoStream CNN网络顾名思义分为两个部分， 1. 空间流处理RGB图像，得到形状信息; 1. 时间流/光流处理光流图像，得到运动信息。 两个流最后经过softmax后，做分类分数的融合，...

引言与背景 蒙特卡洛方法是强化学习中的重要算法类别，它标志着从基于模型到无模型算法的转变。这类算法不依赖环境模型，而是通过与环境的直接交互获取经验数据来学习最优策略。 蒙特卡洛方法在强化学习算法谱系中处于"无模型"方法的起始位置，是从基于模型的方法（如值迭代和策略迭代）向无模型方法过渡的第一步。 无模型强化学习的核心理念可以简述为：如果没有模型，我们必须有数据；如果没有数据，我们必须有模型；如果两者都没有，我们就无法找到最优策略。在强化学习中，"数据"通常指智能体与环境交互的经验。 均值估计问题 在介绍蒙特卡洛强化学习算法之前，我们首先需要理解均值估计问题，这是理解从数据而非模型中学习的基础。 考虑一个可以取有限实数集合 X 中值的随机变量 X ，我们的任务是计算 X 的均值或期望值： E[...

给定一个包含 n 维数据 x 的数据集 D , 简单起见，假设数据 [Math] . 由于真正对联合分布建模的时候， x，y 都是随机变量，故而只需讨论 p(X)=p(x_1,...,x_n) 即可，毕竟只需要令 x_n=y 即可。 给定一个具体的任务，如MNIST中的手写数字二值图分类，从Generative的角度进行Represent，并在Inference中Learning. 下面先介绍： 描述如何对这个MINST任务建模 p(X,Y) （Representation） 对MNIST任务建模 对于一张pixel为 [Math] 大小的图片，令 x_1 表示第一个pixel的随机变量， [Math] ，需明确： 任务目标：学习一个模型分布 [Math] ，使采样时 [Math] ， x ...

引言与背景 价值函数方法是强化学习中的核心技术，它解决了传统表格方法在处理大型状态或动作空间时的效率问题。本文探讨了从表格表示向函数表示的转变，这是强化学习算法发展的重要里程碑。 在强化学习的发展路径中，价值函数方法位于从基于模型到无模型、从表格表示到函数表示的演进过程中。它结合了时序差分学习的思想，并通过函数近似技术来处理复杂环境。 价值表示：从表格到函数 表格与函数表示的对比 传统的表格方法将状态值存储在一个表格中： 而函数近似方法则使用参数化函数来表示这些值，例如： [公式] 其中 [Math] 称作是状态 s 的特征向量， w 是参数向量。 两种不同的表现形式的区别主要体现在以下几个方面： 值的检索方式 值的更新方式 函数复杂度与近似能力 函数的复杂度决定了其近似的能力： 一阶线性函...

引言 时序差分（TemporalDifference，TD）方法是强化学习中的一类核心算法，它结合了动态规划与蒙特卡洛方法的优点。TD方法是无模型（modelfree）学习方法，不需要环境模型即可学习价值函数和最优策略。 TD方法的核心特点是通过比较不同时间步骤的估计值之间的差异来更新价值函数，这种差异被称为"时序差分误差"（TD error）。TD方法可以被视为解决贝尔曼方程或贝尔曼最优方程的特殊随机逼近算法。 基础TD算法：状态值函数学习 给定策略 [Math] ，基础TD算法用于估计状态值函数 [Math] 。假设我们有一些按照策略 [Math] 生成的经验样本 (s_0, r_1, s_1, ..., s_t, r_{t+1}, s_{t+1}, ...) ，TD算法的更新规则为： ...