INCOMING TRANSMISSION

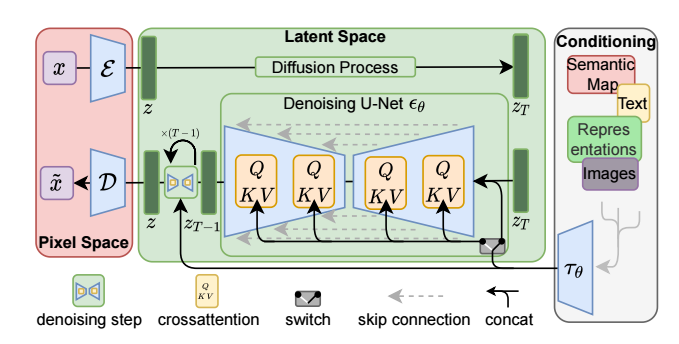
SD模型原理 SD是CompVis、Stability AI和LAION等公司研发的一个文生图模型，它的模型和代码是开源的，而且训练数据LAION5B也是开源的。SD在开源90天github仓库就收获了33K的stars，可见这个模型是多受欢迎。 SD是一个基于latent的扩散模型，它在UNet中引入text condition来实现基于文本生成图像。SD的核心来源于Latent Diffusion这个工作，常规的扩散模型是基于pixel的生成模型，而Latent Diffusion是基于latent的生成模型，它先采用一个autoencoder将图像压缩到latent空间，然后用扩散模型来生成图像的latents，最后送入autoencoder的decoder模块就可以得到生成的图像。 ...

引言与背景 蒙特卡洛方法是强化学习中的重要算法类别，它标志着从基于模型到无模型算法的转变。这类算法不依赖环境模型，而是通过与环境的直接交互获取经验数据来学习最优策略。 蒙特卡洛方法在强化学习算法谱系中处于"无模型"方法的起始位置，是从基于模型的方法（如值迭代和策略迭代）向无模型方法过渡的第一步。 无模型强化学习的核心理念可以简述为：如果没有模型，我们必须有数据；如果没有数据，我们必须有模型；如果两者都没有，我们就无法找到最优策略。在强化学习中，"数据"通常指智能体与环境交互的经验。 均值估计问题 在介绍蒙特卡洛强化学习算法之前，我们首先需要理解均值估计问题，这是理解从数据而非模型中学习的基础。 考虑一个可以取有限实数集合 X 中值的随机变量 X ，我们的任务是计算 X 的均值或期望值： E[...

基础概念 GridWord Example 环境描述：网格世界是一个直观的二维环境，包含： 任务目标： 什么是强化学习：依据策略执行动作感知状态得到奖励 所谓强化学习(Reinforcement Learning，简称RL)，是指基于智能体在复杂、不确定的环境中最大化它能获得的奖励，从而达到自主决策的目的。 a computational approach to learning whereby an agent tries to maximize the total amount of reward it receives while interacting with a complex and uncertain environment 经典的强化学习模型可以总结为下图的形式（你可以理解...

引言与背景 FlashAttention的关键创新在于使用类似于在线Softmax的思想来对自注意力计算进行分块（tiling），从而能够融合整个多头注意力层的计算，而无需访问GPU全局内存来存储中间的logits和注意力分数 在深度学习中，Transformer模型的自注意力机制是计算密集型操作。传统实现需要在GPU全局内存中存储大量中间结果，这导致： 内存瓶颈：中间矩阵占用大量显存 I/O开销：频繁的全局内存访问降低效率 扩展性限制：难以处理超长序列 FlashAttention通过算法创新解决了这些问题。 SelfAtention 自注意力机制的计算可以总结为（为简化说明，忽略头数和批次维度，也省略注意力掩码和缩放因子 [Math] ）： [公式] 其中： Q, K, V, O 都是形...

背景 RLHF 通常包括三个阶段： 有监督微调（SFT） 奖励建模阶段 （Reward Model） RL微调阶段 直接偏好优化（DPO） 传统的RLHF方法分两步走： 1. 先训练一个奖励模型来判断哪个回答更好 1. 然后用强化学习让语言模型去最大化这个奖励 这个过程很复杂，就像绕了一大圈：先学习"什么是好的"，再学习"如何做好"。 DPO发现了一个数学上的捷径： 1. 关键发现：对于任何奖励函数，都存在一个对应的最优策略（语言模型）；反过来说，任何语言模型也隐含着一个它认为最优的奖励函数 1. 直接优化：与其先训练奖励模型再训练语言模型，不如直接训练语言模型，让它自己内化"什么是好的" 1. 数学转换：DPO将"学习判断好坏"和"学习生成好内容"这两个任务合二为一，通过一个简单的数学变换...

模型概述 KimiVL 是一个高效的开源混合专家视觉语言模型(VLM)，它提供先进的多模态推理、长上下文理解和强大的代理能力，同时在语言解码器中仅激活 2.8B 参数(KimiVLA3B)。该模型在多种挑战性任务中表现出色，包括一般用途的视觉语言理解、多轮代理任务、大学水平的图像和视频理解、OCR、数学推理和多图像理解等. 模型架构 KimiVL 的架构由三个主要部分组成： MoE语言模型 Moonlight MoE language model with only 2.8B activated (16B total) parameters 视觉模型 400M nativeresolution MoonViT vision encoder. MLP Projector MoonViT: 原生...

原理分析 网络架构: 本文的任务是Object detection，用到的工具是Transformers，特点是Endtoend。 目标检测的任务是要去预测一系列的Bounding Box的坐标以及Label， 现代大多数检测器通过定义一些proposal，anchor或者windows，把问题构建成为一个分类和回归问题来间接地完成这个任务。文章所做的工作，就是将transformers运用到了object detection领域，取代了现在的模型需要手工设计的工作，并且取得了不错的结果。在object detection上DETR准确率和运行时间上和Faster RCNN相当；将模型 generalize 到 panoptic segmentation 任务上，DETR表现甚至还超过了其他...

摘掉Softmax 制约Attention性能的关键因素，其实是定义里边的Softmax！事实上，简单地推导一下就可以得到这个结论。 [Math] 这一步我们得到一个 [Math] 的矩阵，就是这一步决定了Attention的复杂度是 [Math] ；如果没有Softmax，那么就是三个矩阵连乘 [Math] ，而矩阵乘法是满足结合率的，所以我们可以先算 [Math] ，得到一个 [Math] 的矩阵，然后再用 [Math] 左乘它，由于 [Math] ，所以这样算大致的复杂度只是 [Math] （就是 [Math] 左乘那一步占主导）。 也就是说，去掉Softmax的Attention的复杂度可以降到最理想的线性级别 [Math] ！这显然就是我们的终极追求：Linear Attentio...

概述 本文介绍一个比较有意思的高效Transformer工作——来自Google的《Transformer Quality in Linear Time》，经过细读之后，笔者认为论文里边真算得上是“惊喜满满”了～ 什么样的结果值得我们用“惊喜”来形容？有没有言过其实？我们不妨先来看看论文做到了什么： 1. 提出了一种新的Transformer变体，它依然具有二次的复杂度，但是相比标准的Transformer，它有着更快的速度、更低的显存占用以及更好的效果； 1. 提出一种新的线性化Transformer方案，它不但提升了原有线性Attention的效果，还保持了做Decoder的可能性，并且做Decoder时还能保持高效的训练并行性。 说实话，笔者觉得做到以上任意一点都是非常难得的，而这篇论...

引言 DDPG同样使用了ActorCritic的结构，Deterministic的确定性策略是和随机策略相对而言的，对于某一些动作集合来说，它可能是连续值，或者非常高维的离散值，这样动作的空间维度极大。如果我们使用随机策略，即像DQN一样研究它所有的可能动作的概率，并计算各个可能的动作的价值的话，那需要的样本量是非常大才可行的。于是有人就想出使用确定性策略来简化这个问题。 作为随机策略，在相同的策略，在同一个状态 s 处，采用的动作 [Math] 是基于一个概率分布的，即是不确定的。而确定性策略则决定简单点，虽然在同一个状态处，采用的动作概率不同，但是最大概率只有一个，如果我们只取最大概率的动作，去掉这个概率分布，那么就简单多了。即作为确定性策略，相同的策略，在同一个状态处，动作是唯一确定的...

引言与背景 价值函数方法是强化学习中的核心技术，它解决了传统表格方法在处理大型状态或动作空间时的效率问题。本文探讨了从表格表示向函数表示的转变，这是强化学习算法发展的重要里程碑。 在强化学习的发展路径中，价值函数方法位于从基于模型到无模型、从表格表示到函数表示的演进过程中。它结合了时序差分学习的思想，并通过函数近似技术来处理复杂环境。 价值表示：从表格到函数 表格与函数表示的对比 传统的表格方法将状态值存储在一个表格中： 而函数近似方法则使用参数化函数来表示这些值，例如： [公式] 其中 [Math] 称作是状态 s 的特征向量， w 是参数向量。 两种不同的表现形式的区别主要体现在以下几个方面： 值的检索方式 值的更新方式 函数复杂度与近似能力 函数的复杂度决定了其近似的能力： 一阶线性函...

最优策略（Optimal Policy ） 之前在 贝尔曼方程中说过，状态值可以用来评估一个策略是好是坏，这里给出正式的概念： [公式] 那么此时 [Math] 比 [Math] ”更好“ 最优状态值（Optimal State Value）： 最优策略（Optimal Policy）： 性质： 为了说明上述性质， 我们研究贝尔曼最优方程 Bellman optimality equation（BOE） 贝尔曼最优方程（BOE） 定义 分析最优策略和最优状态值的工具是贝尔曼最优方程（BOE）。通过求解此方程，我们可以获得最优策略和最优状态值。 对于每个 s∈S ，BOE 的elementwise表达式为: [公式] 其中， v(s) 和 [Math] 是待求解的未知变量， π(s) 表示状态...