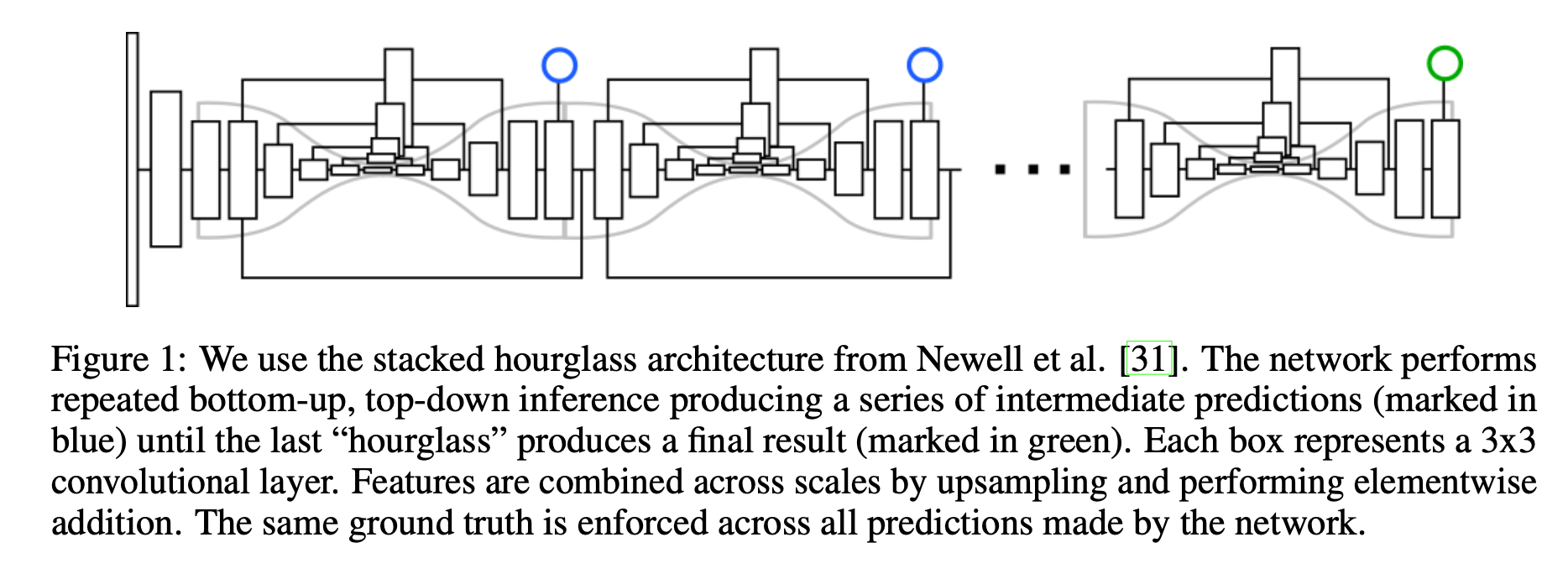
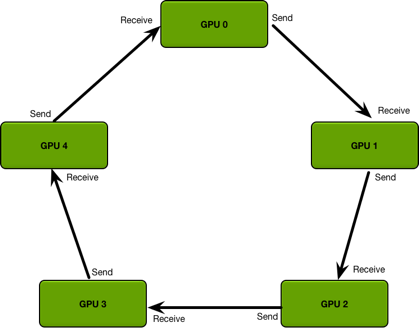
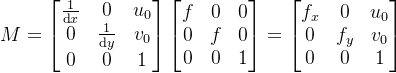3D Model
2026-01-11
三维深度学习简介 多视角(multiview):通过多视角二维图片组合为三维物体,此方法将传统CNN应用于多张二维视角的图片,特征被view pooling procedure聚合起来形成三维物体; 体素(volumetric):通过将物体表现为空间中的体素进行类似于二维的三维卷积(例如,卷积核大小为5x5x5),是规律化的并且易于类比二维的,但同时因为多了一个维度出来,时间和空间复杂度都非常高,目前已经不是主流的方法了; 点云(point clouds):直接将三维点云抛入网络进行训练,数据量小。主要任务有分类、分割以及大场景下语义分割; 非欧式(manifold,graph):在流形或图的结构上进行卷积,三维点云可以表现为mesh结构,可以通过点对之间临接关系表现为图的结构。 点云的特性...