INCOMING TRANSMISSION

Pycharm 的图形化界面虽然好用，但是在某些场景中，是无法使用的。而 Python 本身已经给我们提供了一个调试神器 pdb. 准备文件 在调试之前先将这两个文件准备好（做为演示用），并放在同级目录中。 utils.py [代码] pdb_demo.py [代码] 进入调试模式 主要有两种方法 做为脚本调用，方法很简单，就像正常执行python脚本一样，只是多加了m pdb [代码] 使用这个方式进入调试模式，会在脚本的第一行开始单步调试。 对于单文件的脚本并没有什么问题，如果是一个大型的项目，项目里有很多的文件，使用这种方式只能大大降低我们的效率。 一般情况下，都会直接在你需要的地方打一个断点，那如何打呢？ 只需在你想要打断点的地方加上这两行。 [代码] 然后执行时，也不需要再指定m ...

通过继承创建的新类称为“子类”或“派生类”，被继承的类称为“基类”、“父类”或“超类”，继承的过程，就是从一般到特殊的过程。在某些 OOP 语言中，一个子类可以继承多个基类。但是一般情况下，一个子类只能有一个基类，要实现多重继承，可以通过多级继承来实现 python2中经典类和新式类的继承方式不同，经典类采用深度优先搜索的继承，新式类采用的是广度优先搜索的继承方式 python3中经典类和新式类的继承方式都采用的是都采用广度优先搜索的继承方式 [代码] [代码] 举个例子来说明：现有4个类，A,B,C,D类，D类继承于B类和C类，B类与C类继承于A类。class D(B,C) 实例化D类 深度优先 现在构造函数的继承情况为： 若D类有构造函数，则重写所有父类的继承 若D类没有构造函数，B类有...

Python程序中存储的所有数据都是对象，每一个对象有一个身份，一个类型和一个值。 看变量的实际作用，执行a = 8 这行代码时，就会创建一个值为8的int对象。 变量名是对这个"一个值为8的int对象"的引用。（也可以简称a绑定到8这个对象） 1、可以通过id()来取得对象的身份 这个内置函数，它的参数是a这个变量名，这个函数返回的值 是这个变量a引用的那个"一个值为8的int对象"的内存地址。 [代码] 2、可以通过type()来取得a引用对象的数据类型 [代码] 3、对象的值 当变量出现在表达式中，它会被它引用的对象的值替代。 总结：类型是属于对象，而不是变量。变量只是对对象的一个引用。 对象有可变对象和不可变对象之分。 Python函数传递参数到底是传值还是引用？ 传值、引用这个是c...

问题表示 有很多概率问题，尤其是独立重复实验问题，如果用生成函数的方法来做，会显得特别方便。本文要讲的“随机游走”问题便是其中一例，它又被形象地叫做“醉汉问题”，其本质上是一个二项分布，但是由于取了极限，出现了很多新的性质和应用。我们先考虑如下问题： 考虑实数轴上的一个粒子，在 t=0 时刻它位于原点，每过一秒，它要不向前移动一格（+1），要不就向后移动一格（1），问 n 秒后它所处位置的概率分布。 不难发现，这个问题跟二项分布是雷同的。如果把这个粒子形象比喻成一个“喝醉酒的人”，那么上面的走法就类似于一个完全不省人事的醉汉走路问题了。（当然，醉汉是在三维空间走路的，这里简单起见，只描述了一维...

问题定义 多元二次多项式，维度为 n ，那么可以用以下公式描述该函数： [Formula] 其中 a_{i,j} 为二次项系数，共有 n^2 项， 1≤i,j≤n ，且所有的 a 不全为0，即 ∃a_{i,j}≠0 ; b_k 为一次项系数，共 n 项， 1≤k≤n ; c 为常数项。 记 f(x)=[x_1,x_2,...,x_n]^T ，则上述函数可以写作二次型的形式： 转化过程中A,b满足： A 为n阶对称方阵， A_{i,j}=a_{i,j} 因为 ∃a_{i,j}≠0 ，A不为零矩阵 b_i=b_i 为了后续计算简便，我们将二次型稍作改动： [Formula] 我们的目标就是寻找该函...

基本概念 方向导数：是一个数；反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 偏导数：是多个数（每元有一个）；是指多元函数沿坐标轴方向的方向导数，因此二元函数就有两个偏导数。 偏导函数：是一个函数；是一个关于点的偏导数的函数。 梯度：是一个向量；每个元素为函数对一元变量的偏导数；它既有大小（其大小为最大方向导数），也有方向。 方向导数 反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 例子如下： 题目 设二元函数 f(x, y) = x^2 + y^2 ，分别计算此函数在点 (1, 2) 沿方向 w=\{3, 4\} 与方向 u=\{1, 0\} 的方向导数。 解： ...

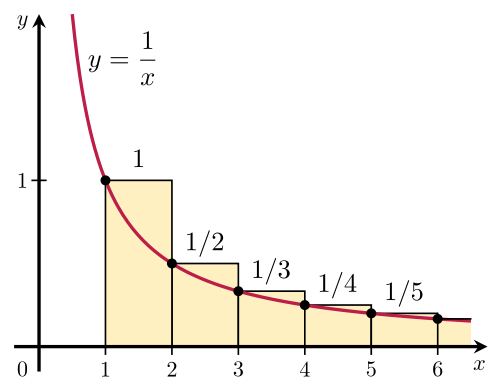
调和级数记住下面的公式就够了： [Formula] 证明方法就是下面这张图

一、泊松分布 日常生活中，大量事件是有固定频率的。 某医院平均每小时出生3个婴儿 某公司平均每10分钟接到1个电话 某超市平均每天销售4包xx牌奶粉 某网站平均每分钟有2次访问 它们的特点就是，我们可以预估这些事件的总数，但是没法知道具体的发生时间。已知平均每小时出生3个婴儿，请问下一个小时，会出生几个？ 有可能一下子出生6个，也有可能一个都不出生。这是我们没法知道的。 泊松分布就是描述某段时间内，事件具体的发生概率。 [Formula] 上面就是泊松分布的公式。等号的左边， P 表示概率， N 表示某种函数关系， t 表示时间， n 表示数量，1小时内出生3个婴儿的概率，就表示为 P(N(1...

概述 HiPPO（Highorder Polynomial Projection Operators）是目前大热的structured state space model (S4)及其后续工作的backbone. State space mode主要是控制学科里的内容，最近被引入深度学习领域来解决长距离依赖问题。长距离依赖建模的核心问题是如何通过有限的memory来尽可能记住之前所有的历史信息。当前的主流序列建模模型（即Transformer和RNN) 存在着普遍的遗忘问题 fixedsize context windows: Transformer的window size通常是有限的，一般来说quadratic的attention最多建模到大约10k的token就到计算极限了 vanish...