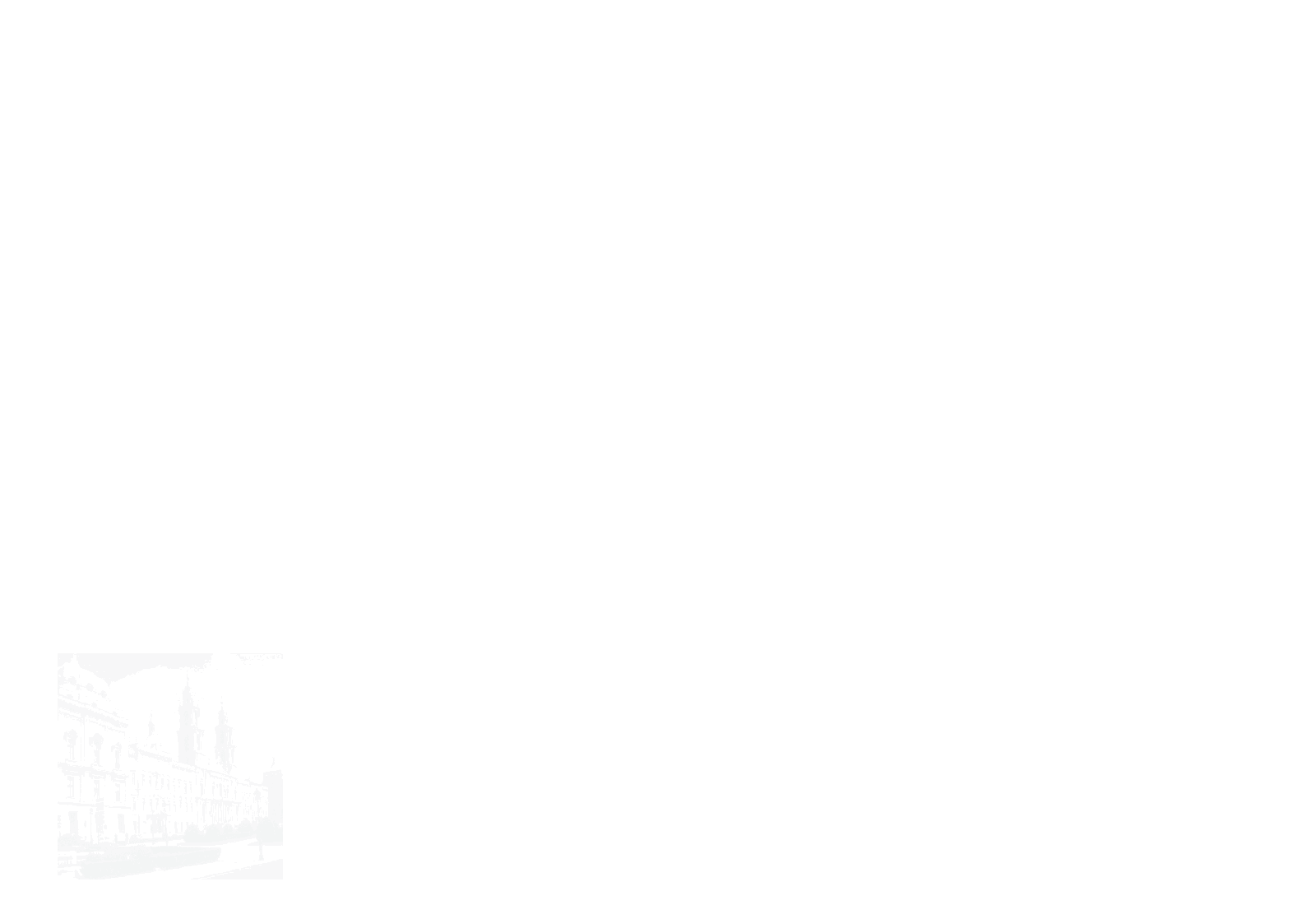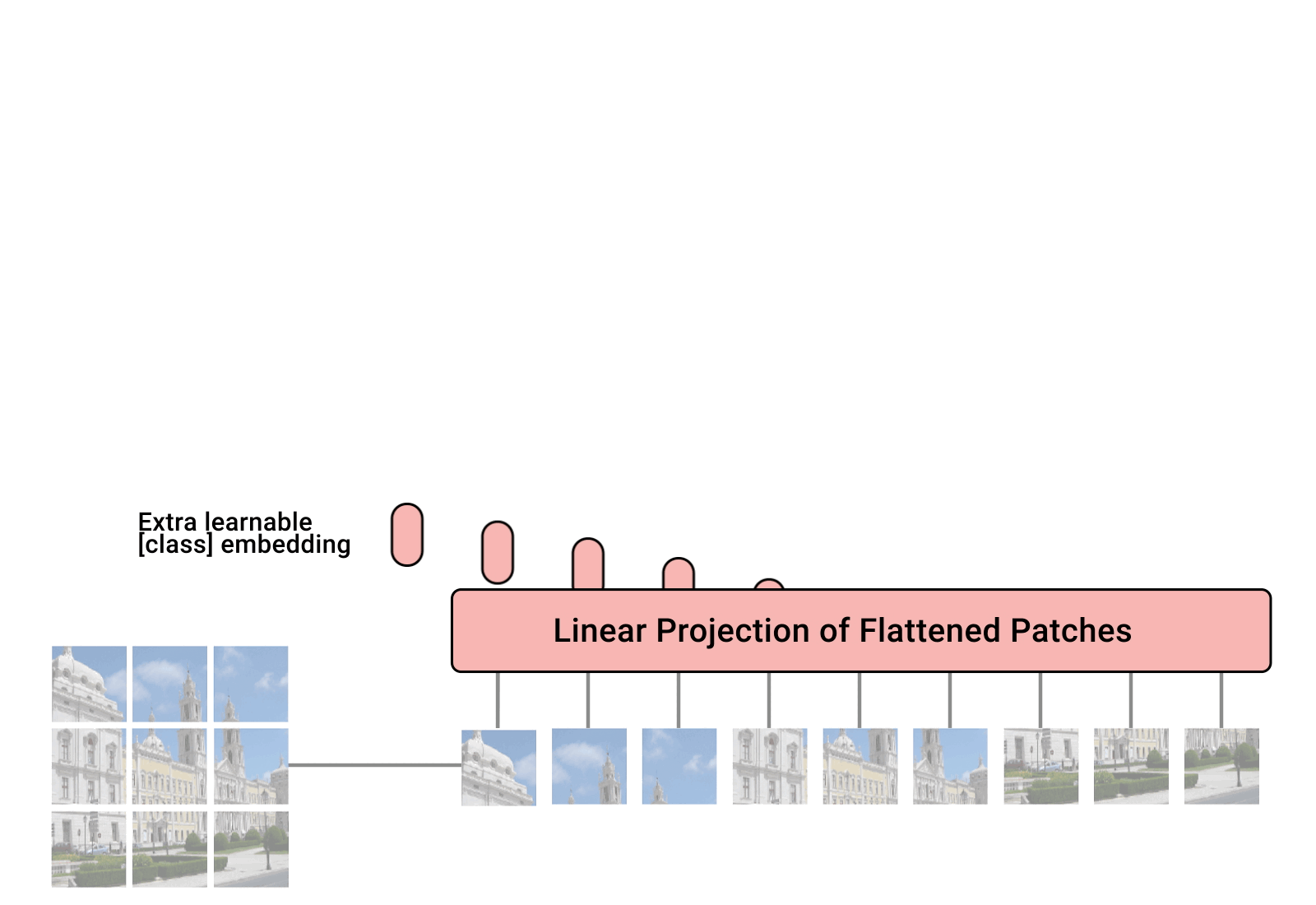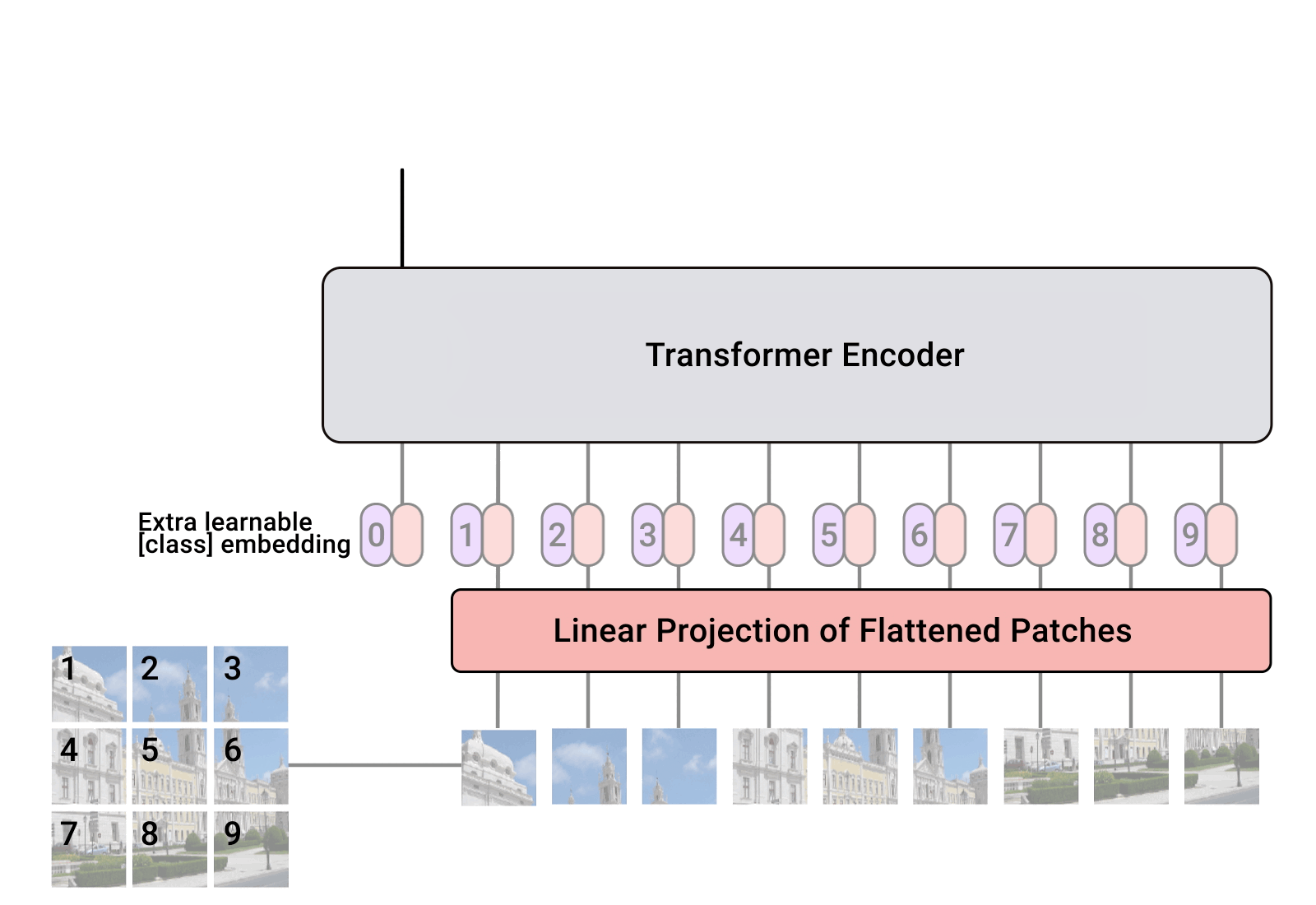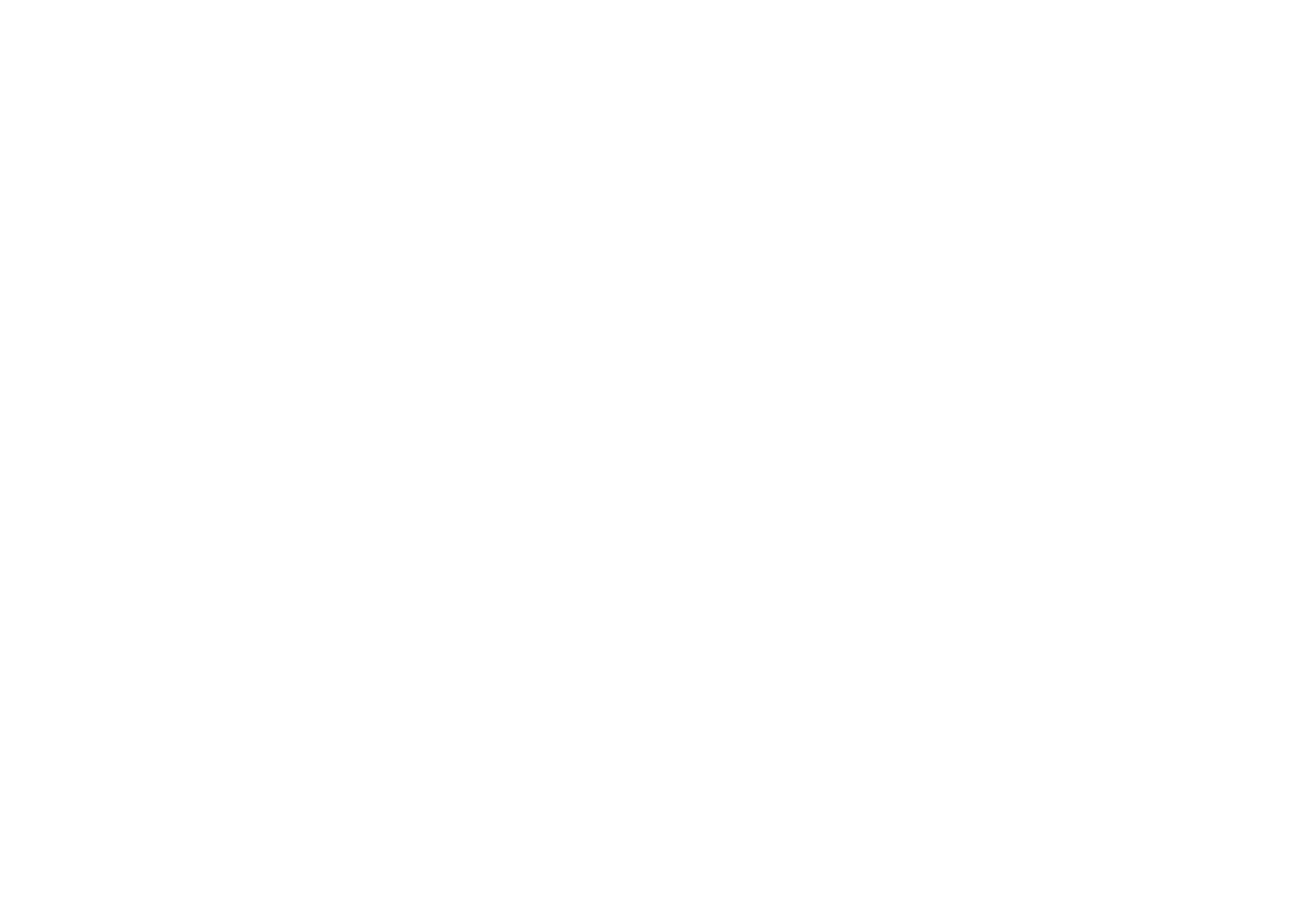INCOMING TRANSMISSION

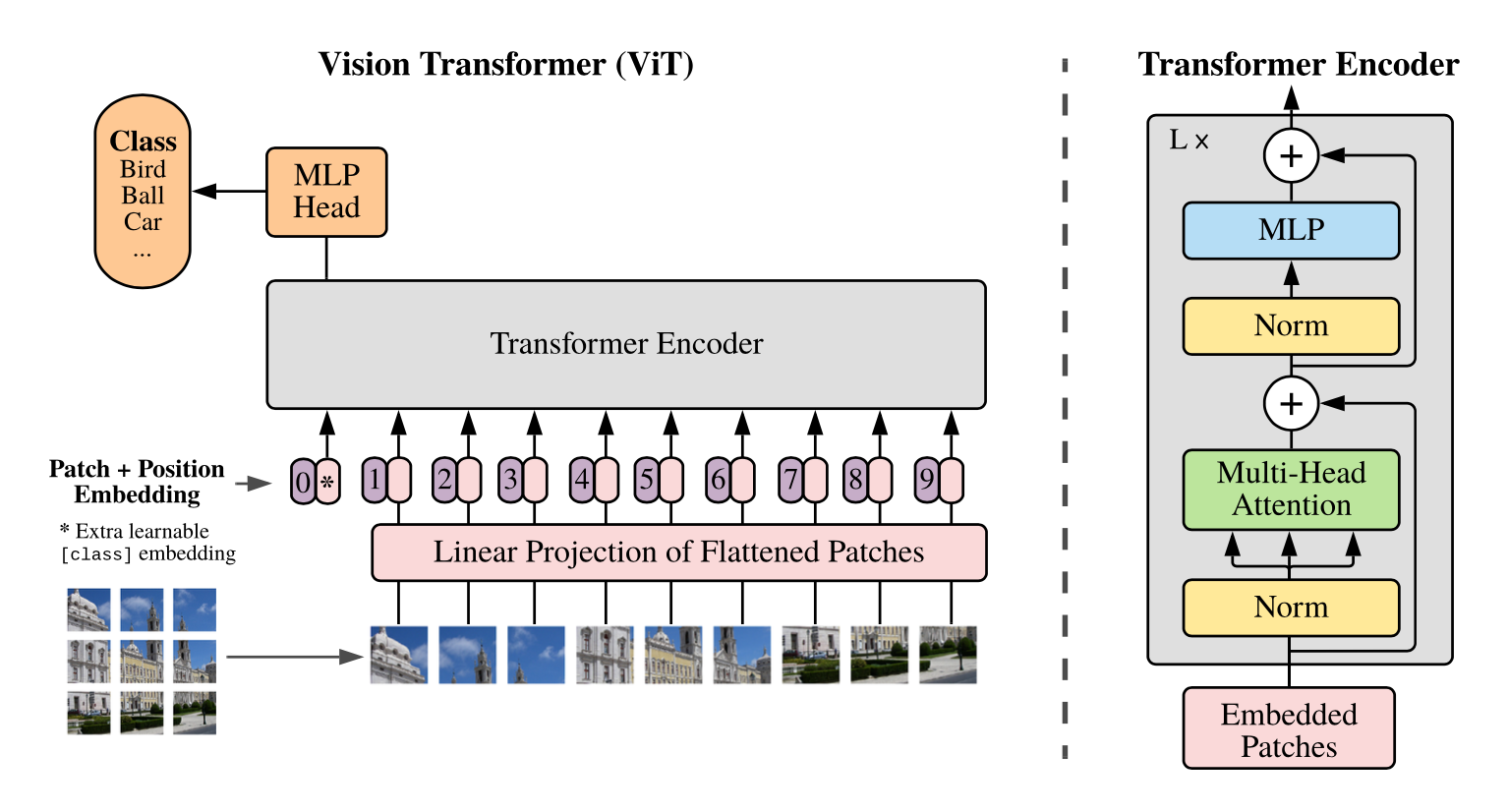
概述 在计算机视觉领域（CV），对视觉特征的理解CNN是长期处于主导地位的。而在NLP领域，Transformer框架的巨大成功，也激发了不少研究者探索将Transformer用于计算机视觉任务。ViT（Vision Transformer）的出现标志着在CV领域Transformer架构迈出了重要的一步。尤其在当前结合LLM的多模态探索上（MM-LLM），都是以LLM大语言模型为骨干架构的模型，多种模态的信息需要先做token化处理，再输入到LLM模型。ViT天然具有序列化特征的建模能力，自然在MM-LLM探索中大放异彩~ ViT在多模态模型中的角色类似于自然语言建模中的Tokenizer组件，对图像进行视觉特征编码，产出图像的序列特征。只不过ViT的编码过程本身也是采用了Transformer的模型结构。 本文主要结合几篇paper和源码讲讲ViT和针对ViT的一些优化方法~ ViT（Vision Transformer）...

ViT（vision transformer）是Google在2020年提出的直接将transformer应用在图像分类的模型，后面很多的工作都是基于ViT进行改进的。ViT的思路很简单：直接把图像分成固定大小的patchs，然后通过线性变换得到patch embedding，这就类比NLP的words和word embedding，由于transformer的输入就是a sequence of token embeddings，所以将图像的patch embeddings送入transformer后就能够进行特征提取从而分类了。ViT模型原理如下图所示，其实ViT模型只是用了transformer的Encoder来提取特征（原始的transformer还有decoder部分，用于实现sequence to sequence，比如机器翻译）。下面将分别对各个部分做详细的介绍。 Patch Embedding 对于ViT来说，首先要将原始的2-D图像转换成一系列1-D的patch embeddings，这就好似NLP中的word embedding。输入的2-D图像记为 \(x\in...

简介 如果以概率的视角看待世界的生成模型。 在这样的世界观中，我们可以将任何类型的观察数据（例如 \(D\) ）视为来自底层分布（例如 \( p_{data}\) ）的有限样本集。 任何生成模型的目标都是在访问数据集 \(D\) 的情况下近似该数据分布。 如果我们能够学习到一个好的生成模型，我们可以将学习到的模型用于下游推理。 我们主要对数据分布的参数近似感兴趣，在一组有限的参数中，它总结了关于数据集 \(D\) 的所有信息。 与非参数模型相比，参数模型在处理大型数据集时能够更有效地扩展，但受限于可以表示的分布族。 在参数的设置中，我们可以将学习生成模型的任务视为在模型分布族中挑选参数，以最小化模型分布和数据分布之间的距离。 如上图，给定一个狗的图像数据集，我们的目标是学习模型族 \(M\) 中生成模型 θ 的参数，使得模型分布 \(p_θ\) 接近 \(p_{data}\) 上的数据分布。 在数学上，我们可以将我们的目标指定为以下优化问题: \[\mathop{min}\limits_{\theta\in M}d(p_\theta,p_{data})\] 其中， \(d()\)...

研究对象与基本设定 我们希望学习一个能够“生成数据”的概率模型。假设我们有一个数据集 \(D\) ，每个样本是 \(n\) 维二值向量： \(x \in \{0,1\}^n\) 我们的目标是用一个参数化分布 \(p_\theta(x)\) 去逼近真实数据分布 \(p_{\text{data}}(x)\) ，并最终能够： 密度估计 ：给定 \(x\) 计算 \(p_\theta(x)\) 或 \(\log p_\theta(x)\) 采样生成 ：从 \(p_\theta(x)\) 采样得到新的 \(x\) 表示：链式法则与自回归分解 链式法则分解联合分布 任意联合分布都可用概率链式法则分解为条件概率的乘积： \[p(x) = \prod_{i=1}^{n} p(x_i \mid x_1, x_2, \dots, x_{i-1}) = \prod_{i=1}^{n} p(x_i \mid x_{<i})\] 其中： \(x_{<i} = [x_1, x_2, \dots, x_{i-1}]\) ，这意味着：只要我们能为每个维度 \(i\) 学好一个条件分布 \(p(x_i \mid...

the machine predicts any parts of its input for any observed part 这是LeCun在AAAI 2020上对自监督学习的定义，再结合传统的自监督学习定义，可以总结如下两点特征： 通过“半自动”过程从数据本身获取“标签”； 从“其他部分”预测部分数据。 个人理解， 其实任意挖掘对象之间联系、探索不同对象共同本质的方法，都或多或少算是自监督学习的思想 。 自监督学习与无监督学习的区别主要在于，无监督学习专注于检测特定的数据模式，如聚类、社区发现或异常检测，而自监督学习的目标是恢复（recovering），仍处于监督学习的范式中。上图展示了三者之间的区别， 自监督中的“related information” 可以来自其他模态、输入的其他部分以及输入的不同形式。 Self-Supervised...

简介 生成树（spanning tree） 在图论中，无向图 G=(V,E) 的生成树（spanning tree)是具有G的全部顶点，但边数最少的联通子图。假设G中一共有n个顶点，一颗生成树满足下列条件： （1）n个顶点； （2）n1条边； （3）n个顶点联通； （4）一个图的生成树可能有多个。最小生成树（minimum spanning tree， MST）/最小生成森林：联通加权无向图中边缘权重加和最小的生成树。给定无向图 G=(V,E) ， (u,v) 代表顶点 u 与顶点 v 的边， w(u,v) 代表此边的权重，若存在生成树T使得： [公式] 最小，则 T 为 G 的最小生成树。对于非连通无向图来说，它的每一连通分量同样有最小生成树，它们的并被称为最小生成森林。最小生成树除了继承...

给一个无向图，判断其是否为一棵树。如果是树的话，所有的节点必须是连接的，也就是说必须是连通图，而且不能有环，所以就变成了验证是否是连通图和是否含有环。 [代码]

题目 中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。 例如， [2,3,4] 的中位数是 3 [2,3] 的中位数是 (2 + 3) / 2 = 2.5 设计一个支持以下两种操作的数据结构： void addNum(int num) 从数据流中添加一个整数到数据结构中。 double findMedian() 返回目前所有元素的中位数。 示例： addNum(1) addNum(2) findMedian() 1.5 addNum(3) findMedian() 2 题解 维护两个堆：大顶堆和小顶堆。并且需满足如下条件： 小顶堆的所有元素都大于等于大顶堆的所有元素。 大顶堆中的元素数量大于等于小顶堆中的元素数量。 大顶堆对应排序后的列表的左半部分；小顶堆对应排序...

[代码] 自己实现小顶堆 [代码] 变态的需求来了：给出N长的序列，求出BtmK小的元素，即使用大顶堆。 概括一种最简单的： 将push(e)改为push(e)、pop(e)改为pop(e)。 也就是说，在存入堆、从堆中取出的时候，都用相反数，而其他逻辑与TopK完全相同，看代码： [代码] 自己实现大顶堆 [代码]

二叉树结构 [代码] 递归 时间复杂度：O(n)，n为节点数，访问每个节点恰好一次。 空间复杂度：空间复杂度：O(h)，h为树的高度。最坏情况下需要空间O(n)，平均情况为O(logn) 递归1: 二叉树遍历最易理解和实现版本 [代码] 递归2: 通用模板 可以适应不同的题目，添加参数、增加返回条件、修改进入递归条件、自定义返回值 [代码] 迭代 时间复杂度：O(n)，n为节点数，访问每个节点恰好一次。 空间复杂度：O(h)，h为树的高度。取决于树的结构，最坏情况存储整棵树，即O(n) 迭代1: 前序遍历最常用模板（后序同样可以用） [代码] 迭代2: 前、中、后序遍历通用模板（只需一个栈的空间） [代码] 迭代3：标记法迭代（需要双倍的空间来存储访问状态） 前、中、后、层序通用模板，只需改...

背包问题

简介 之前的很多方法都是用RNN的结构去构建时序上的依赖关系，但是RNN的结构的缺点是不能并行操作，且存在梯度消失的现象。所以本文就是将之前的RNN的结构改为Transfomer的形式。延续了之前TRN的整个网络的框架，也是结合了对未来帧的预测与历史帧的表示相结合来对当前的动作进行预测。 方法 整个网络框架如上图所示， Encoder就是利用transfomer对longrange的历史和目前帧进行特征表示，其中要说明的一个点就是，这里的特征空间包含T个历史特征，当前窗口的特征以及一个task token，这个task token的作用可以从下图看出来 这幅图对比的是输入进classifier的特征与网络输入的特征的相似性，可以看出w/o task token 对应的是当前t=0时刻的特征，...