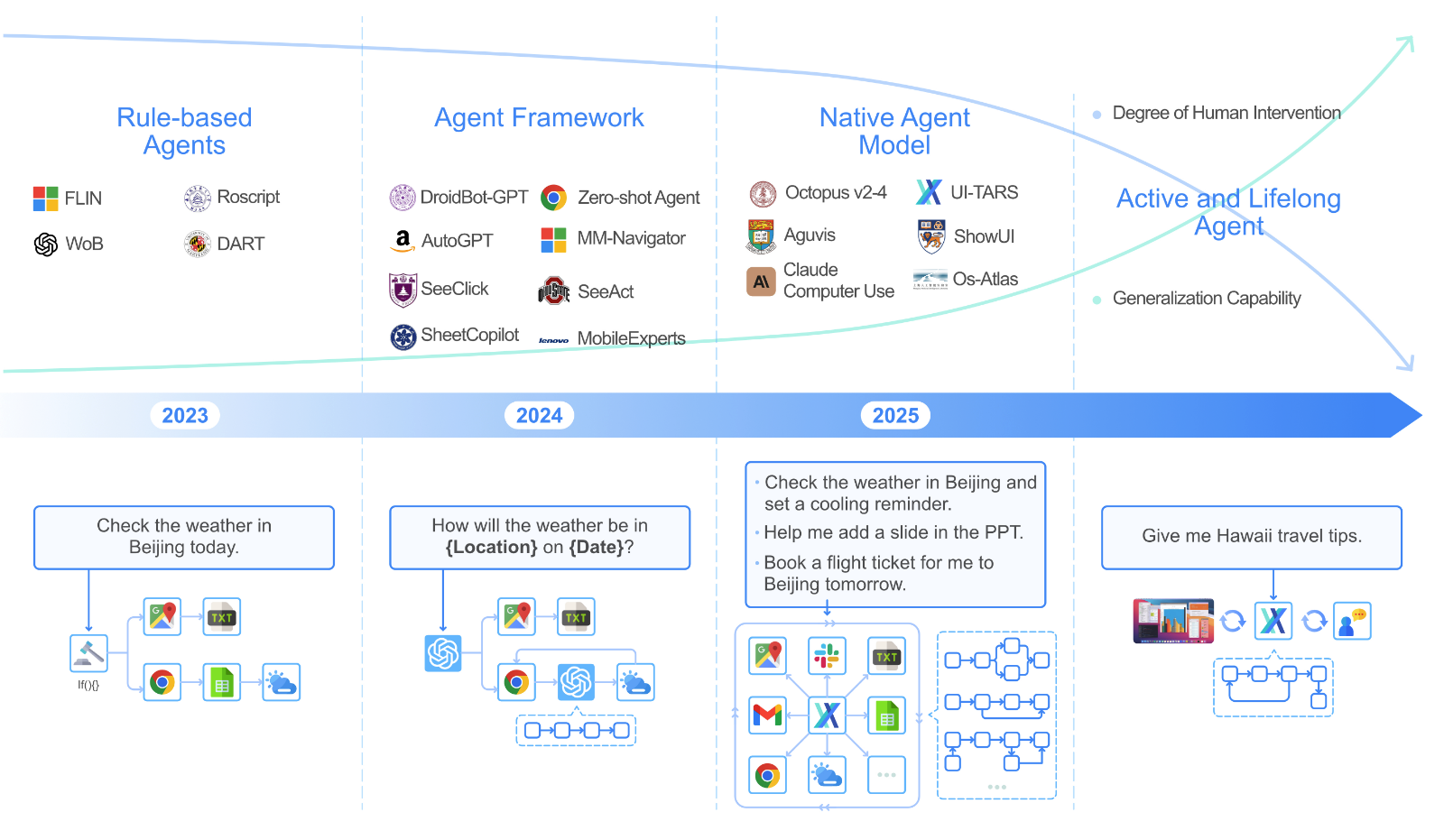
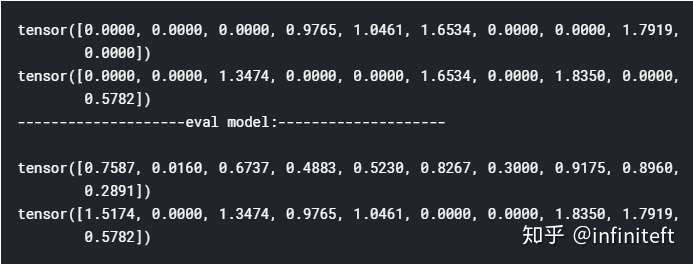
3D Model
2026-01-11
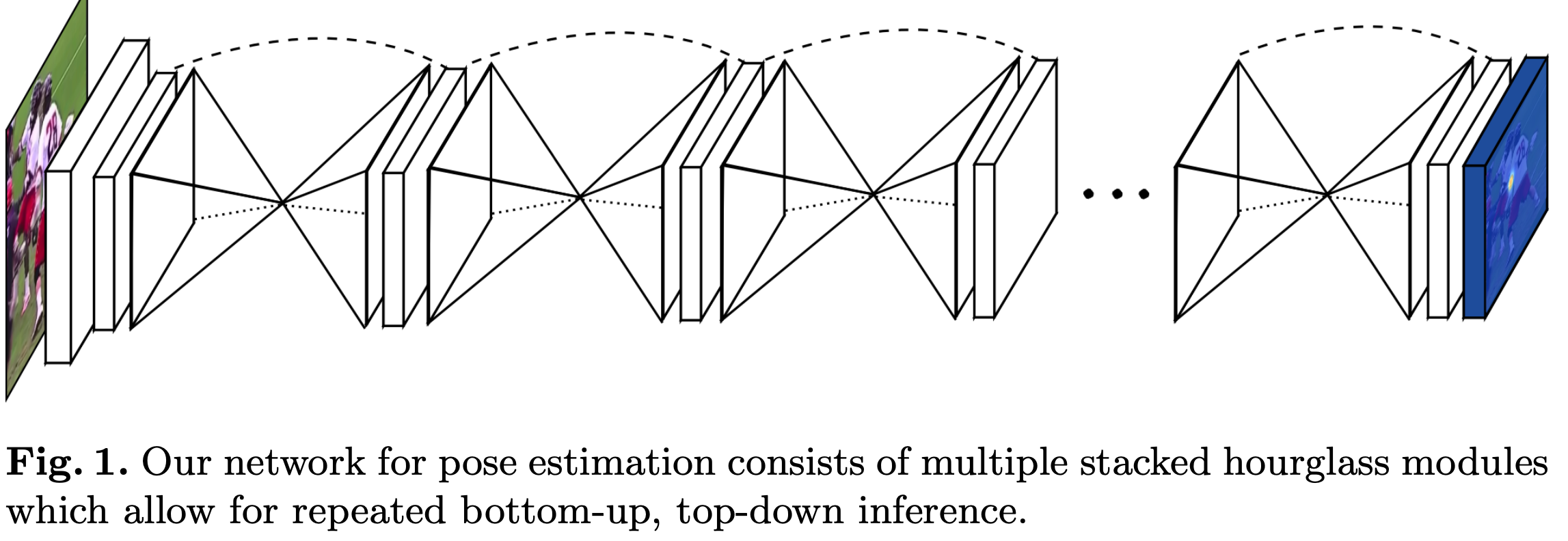
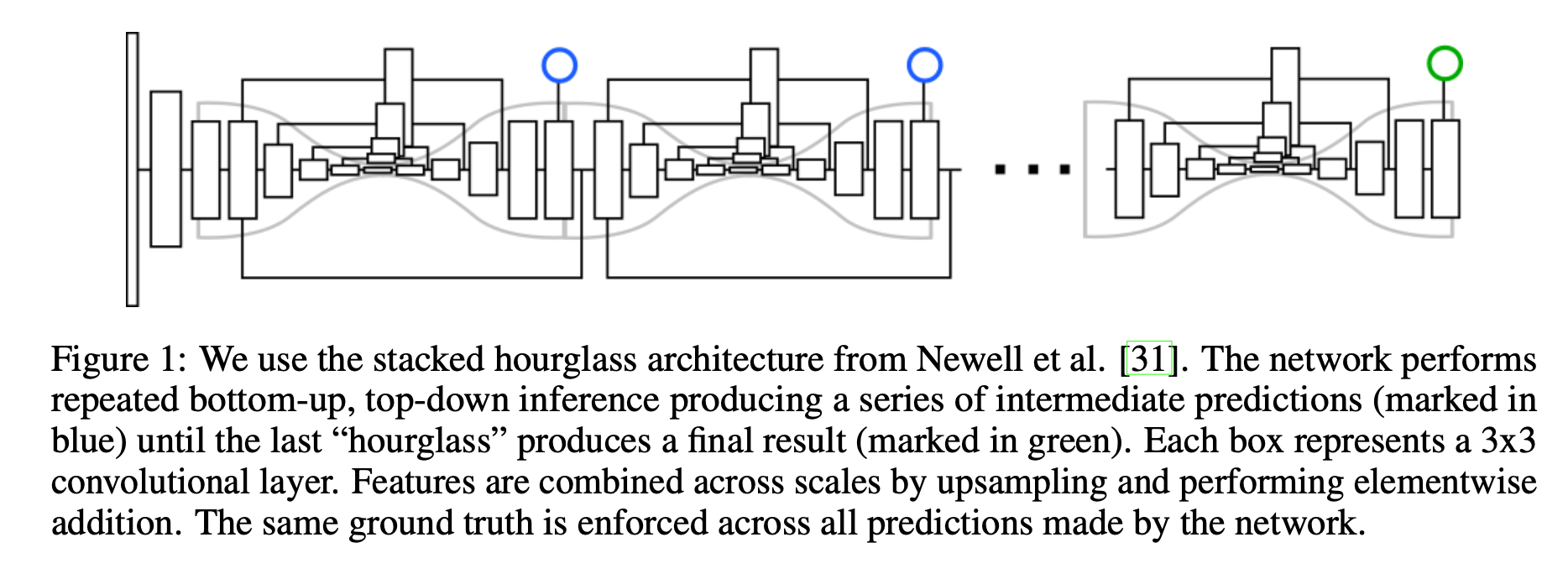
论文介绍了一种新的网络结构用于人体姿态检测,作者在论文中展现了不断重复bottomup、topdown过程以及运用intermediate supervison(中间监督)对于网络性能的提升,下面来介绍Stacked Hourglass Networks. 简介 理解人类的姿态对于一些高级的任务比如行为识别来说特别重要,而且也是一些人机交互任务的基础。作者提出了一种新的网络结构Stacked Hourglass Networks来对人体的姿态进行识别,这个网络结构能够捕获并整合图像所有尺度的信息。之所以称这种网络为Stacked Hourglass Networks,主要是它长得很像堆叠起来的沙漏,如下图所示: 这种堆叠在一起的Hourglass模块结构是对称的,bottomup过程将图片从...