INCOMING TRANSMISSION

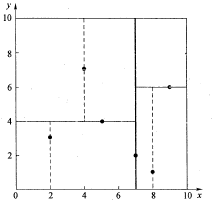
kd树（kdimensional树的简称），是一种分割k维数据空间的数据结构。主要应用于多维空间关键数据的搜索（如：范围搜索和最近邻搜索）。 应用背景 SIFT算法中做特征点匹配的时候就会利用到kd树。而特征点匹配实际上就是一个通过距离函数在高维矢量之间进行相似性检索的问题。针对如何快速而准确地找到查询点的近邻，现在提出了很多高维空间索引结构和近似查询的算法，kd树就是其中一种。 索引结构中相似性查询有两种基本的方式：一种是范围查询（range searches），另一种是K近邻查询（Kneighbor searches）。范围查询就是给定查询点和查询距离的阈值，从数据集中找出所有与查询点距离小于阈值的数据；K近邻查询是给定查询点及正整数K，从数据集中找到距离查询点最近的K个数据，当K=1时...

问题表示 有很多概率问题，尤其是独立重复实验问题，如果用生成函数的方法来做，会显得特别方便。本文要讲的“随机游走”问题便是其中一例，它又被形象地叫做“醉汉问题”，其本质上是一个二项分布，但是由于取了极限，出现了很多新的性质和应用。我们先考虑如下问题： 考虑实数轴上的一个粒子，在 t=0 时刻它位于原点，每过一秒，它要不向前移动一格（+1），要不就向后移动一格（1），问 n 秒后它所处位置的概率分布。 不难发现，这个问题跟二项分布是雷同的。如果把这个粒子形象比喻成一个“喝醉酒的人”，那么上面的走法就类似于一个完全不省人事的醉汉走路问题了。（当然，醉汉是在三维空间走路的，这里简单起见，只描述了一维...

序言 极大似然估计与贝叶斯估计是统计中两种对模型的参数确定的方法，两种参数估计方法使用不同的思想。前者来自于频率派，认为参数是固定的，我们要做的事情就是根据已经掌握的数据来估计这个参数；而后者属于贝叶斯派，认为参数也是服从某种概率分布的，已有的数据只是在这种参数的分布下产生的。所以，直观理解上，极大似然估计就是假设一个参数 θ ，然后根据数据来求出这个 θ . 而贝叶斯估计的难点在于 p(θ) 需要人为设定，之后再考虑结合MAP（maximum a posterior）方法来求一个具体的 θ . 所以极大似然估计与贝叶斯估计最大的不同就在于是否考虑了先验，而两者适用范围也变成了：极大似然估计适用于数据大量，估计的参数能够较好的反映实际情况；而贝叶斯估计则在数据量较少或者比较稀疏的情况下，考虑...

这篇博客介绍一下集成学习的几类：Bagging，Boosting以及Stacking。 传统机器学习算法 (例如：决策树，人工神经网络，支持向量机，朴素贝叶斯等) 的目标都是寻找一个最优分类器尽可能的将训练数据分开。集成学习 (Ensemble Learning) 算法的基本思想就是将多个分类器组合，从而实现一个预测效果更好的集成分类器。集成算法可以说从一方面验证了中国的一句老话：三个臭皮匠，赛过诸葛亮。 Thomas G. Dietterich 指出了集成算法在统计，计算和表示上的有效原因： 统计上的原因 一个学习算法可以理解为在一个假设空间 H 中选找到一个最好的假设。但是，当训练样本的数据量小到不够用来精确的学习到目标假设时，学习算法可以找到很多满足训练样本的分类器。所以，学习算法选择...

引言与背景 FlashAttention的关键创新在于使用类似于在线Softmax的思想来对自注意力计算进行分块（tiling），从而能够融合整个多头注意力层的计算，而无需访问GPU全局内存来存储中间的logits和注意力分数 在深度学习中，Transformer模型的自注意力机制是计算密集型操作。传统实现需要在GPU全局内存中存储大量中间结果，这导致： 内存瓶颈：中间矩阵占用大量显存 I/O开销：频繁的全局内存访问降低效率 扩展性限制：难以处理超长序列 FlashAttention通过算法创新解决了这些问题。 SelfAtention 自注意力机制的计算可以总结为（为简化说明，忽略头数和批次维度，也省略注意力掩码和缩放因子 [Math] ）： [公式] 其中： Q, K, V, O 都是形...

摘掉Softmax 制约Attention性能的关键因素，其实是定义里边的Softmax！事实上，简单地推导一下就可以得到这个结论。 [Math] 这一步我们得到一个 [Math] 的矩阵，就是这一步决定了Attention的复杂度是 [Math] ；如果没有Softmax，那么就是三个矩阵连乘 [Math] ，而矩阵乘法是满足结合率的，所以我们可以先算 [Math] ，得到一个 [Math] 的矩阵，然后再用 [Math] 左乘它，由于 [Math] ，所以这样算大致的复杂度只是 [Math] （就是 [Math] 左乘那一步占主导）。 也就是说，去掉Softmax的Attention的复杂度可以降到最理想的线性级别 [Math] ！这显然就是我们的终极追求：Linear Attentio...

概述 本文介绍一个比较有意思的高效Transformer工作——来自Google的《Transformer Quality in Linear Time》，经过细读之后，笔者认为论文里边真算得上是“惊喜满满”了～ 什么样的结果值得我们用“惊喜”来形容？有没有言过其实？我们不妨先来看看论文做到了什么： 1. 提出了一种新的Transformer变体，它依然具有二次的复杂度，但是相比标准的Transformer，它有着更快的速度、更低的显存占用以及更好的效果； 1. 提出一种新的线性化Transformer方案，它不但提升了原有线性Attention的效果，还保持了做Decoder的可能性，并且做Decoder时还能保持高效的训练并行性。 说实话，笔者觉得做到以上任意一点都是非常难得的，而这篇论...

概述 SSM的概念由来已久，但这里我们特指深度学习中的SSM，一般认为其开篇之作是2021年的 S4，不算太老，而SSM最新最火的变体大概是Mamba。当然，当我们谈到SSM时，也可能泛指一切线性RNN模型，这样RWKV、RetNet还有此前LRU都可以归入此类。不少SSM变体致力于成为Transformer的竞争者，尽管笔者并不认为有完全替代的可能性，但SSM本身优雅的数学性质也值得学习一番。 尽管我们说SSM起源于S4，但在S4之前，SSM有一篇非常强大的奠基之作《HiPPO: Recurrent Memory with Optimal Polynomial Projections》（简称HiPPO），所以本文从HiPPO开始说起。 另外值得一提的是，SSM代表作HiPPO、S4、Mam...

问题定义 多元二次多项式，维度为 n ，那么可以用以下公式描述该函数： [Formula] 其中 a_{i,j} 为二次项系数，共有 n^2 项， 1≤i,j≤n ，且所有的 a 不全为0，即 ∃a_{i,j}≠0 ; b_k 为一次项系数，共 n 项， 1≤k≤n ; c 为常数项。 记 f(x)=[x_1,x_2,...,x_n]^T ，则上述函数可以写作二次型的形式： 转化过程中A,b满足： A 为n阶对称方阵， A_{i,j}=a_{i,j} 因为 ∃a_{i,j}≠0 ，A不为零矩阵 b_i=b_i 为了后续计算简便，我们将二次型稍作改动： [Formula] 我们的目标就是寻找该函...

基本概念 方向导数：是一个数；反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 偏导数：是多个数（每元有一个）；是指多元函数沿坐标轴方向的方向导数，因此二元函数就有两个偏导数。 偏导函数：是一个函数；是一个关于点的偏导数的函数。 梯度：是一个向量；每个元素为函数对一元变量的偏导数；它既有大小（其大小为最大方向导数），也有方向。 方向导数 反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 例子如下： 题目 设二元函数 f(x, y) = x^2 + y^2 ，分别计算此函数在点 (1, 2) 沿方向 w=\{3, 4\} 与方向 u=\{1, 0\} 的方向导数。 解： ...

通常我们训练神经网络模型的时候默认使用的数据类型为单精度FP32。近年来，为了加快训练时间、减少网络训练时候所占用的内存，并且保存训练出来的模型精度持平的条件下，业界提出越来越多的混合精度训练的方法。这里的混合精度训练是指在训练的过程中，同时使用单精度（FP32）和半精度（FP16）。 浮点数据类型 浮点数据类型主要分为双精度（FP64）、单精度（FP32）、半精度（FP16）。在神经网络模型的训练过程中，一般默认采用单精度（FP32）浮点数据类型，来表示网络模型权重和其他参数。在了解混合精度训练之前，这里简单了解浮点数据类型。 根据IEEE二进制浮点数算术标准（IEEE 754）的定义，浮点数据类型分为双精度（FP64）、单精度（FP32）、半精度（FP16）三种，其中每一种都有三个不同的...

概述 众所周知，尽管基于Attention机制的Transformer类模型有着良好的并行性能，但它的空间和时间复杂度都是 [Math] 级别的， n 是序列长度，所以当 n 比较大时Transformer模型的计算量难以承受。近来，也有不少工作致力于降低Transformer模型的计算量，比如模型剪枝、量化、蒸馏等精简技术，又或者修改Attention结构，使得其复杂度能降低到 [Math] 甚至 [Math] 。 改变这一复杂度的思路主要有两种： 一是走稀疏化的思路，比如OpenAI的Sparse Attention，通过“只保留小区域内的数值、强制让大部分注意力为零”的方式，来减少Attention的计算量。经过特殊设计之后，Attention矩阵的大部分元素都是0，因此理论上它也能节...