INCOMING TRANSMISSION

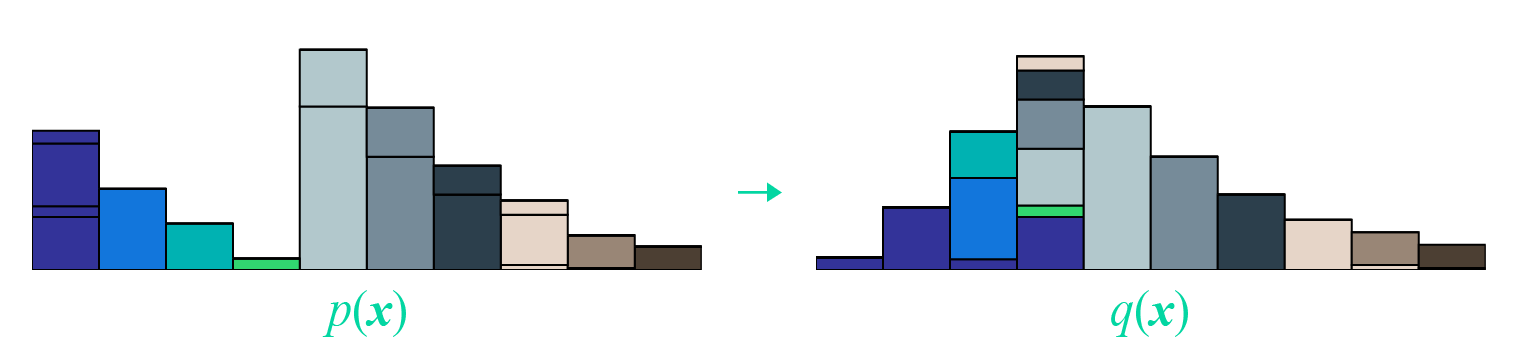
本文受启发于著名的国外博文 《Wasserstein GAN and the Kantorovich-Rubinstein Duality》 ，内容跟它大体上相同，但是删除了一些冗余的部分，对不够充分或者含糊不清的地方作了补充。 Wasserstein距离 显然，整篇文章必然围绕着Wasserstein距离（ \(\mathcal{W}\) 距离）来展开。假设我们有了两个概率分布 \(p(x),q(x)\) ，那么Wasserstein距离的定义为 \[\mathcal{W}[p,q]=\inf_{\gamma\in \Pi[p,q]} \iint \gamma(\boldsymbol{x},\boldsymbol{y}) d(\boldsymbol{x},\boldsymbol{y}) d\boldsymbol{x}d\boldsymbol{y}\] 事实上，这也算是最优传输理论中最核心的定义了。 成本函数 首先 \(d(x,y)\) ，它不一定是距离，其准确含义应该是一个成本函数，代表着从 \(x\) 运输到 \(y\) 的成本。常用的 \(d\) 是基于 \(l\)...

简介 生成对抗网络 ( Generative Adversarial Network, GAN ) 是由 Goodfellow 于 2014 年提出的一种对抗网络。这个网络框架包含两个部分，一个生成模型 (generative model) 和一个判别模型 (discriminative model)。其中，生成模型可以理解为一个伪造者，试图通过构造假的数据骗过判别模型的甄别；判别模型可以理解为一个警察，尽可能甄别数据是来自于真实样本还是伪造者构造的假数据。两个模型都通过不断的学习提高自己的能力，即生成模型希望生成更真的假数据骗过判别模型，而判别模型希望能学习如何更准确的识别生成模型的假数据。 网络框架 GAN 由两部分构成，一个 生成器 ( Generator ) 和一个 判别器 ( Discriminator )。对于生成器，我们需要学习关于数据 \(x\) 的一个分布 \(p_g\) ，首先定义一个输入数据的先验分布 \(p_z(z)\) ，其次定义一个映射 \(G \left(\boldsymbol{z}; \theta_g\right): \boldsymbol{z}...

Normalizing flow（标准化流）是一类对概率分布进行建模的工具，它能完成简单的概率分布（例如高斯分布）和任意复杂分布之间的相互转换，经常被用于 data generation、density estimation、inpainting 等任务中，例如 Stability AI 提出的 Stable Diffusion 3 中用到的 rectified flow 就是 normalizing flow 的变体之一。 为了便于理解，在正式开始介绍之前先简要说明一下 normalizing flow 的做法。如上图所示，为了将一个高斯分布 \(z_0\) 转换为一个复杂的分布 \(z_K\) ，normalizing flow 会对初始的分布 \(z_0\) 进行多次可逆的变换，将其逐渐转换为 \(z_K\) 。由于每一次变换都是可逆的，从 \(z_K\) 出发也能得到高斯分布 \(z_0\) 。这样，我们就实现了复杂分布与高斯分布之间的互相转换，从而能从简单的高斯分布建立任意复杂分布。 对 diffusion models 比较熟悉的读者可能已经发现了，这个过程和...

分布变换 通常我们会拿VAE跟GAN比较，的确，它们两个的目标基本是一致的——希望构建一个从隐变量 \(Z\) 生成目标数据 \(X\) 的模型，但是实现上有所不同。更准确地讲，它们是假设了 \(Z\) 服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型 \(X=g(Z)\) ，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的变换。 生成模型的难题就是判断生成分布与真实分布的相似度，因为我们只知道两者的采样结果，不知道它们的分布表达式 那现在假设 \(Z\) 服从标准的正态分布，那么我就可以从中采样得到若干个 \(Z_1, Z_2, \dots, Z_n\) ，然后对它做变换得到 \(\hat{X}_1 = g(Z_1),\hat{X}_2 = g(Z_2),\dots,\hat{X}_n = g(Z_n)\) ，我们怎么判断这个通过 \(g\)...

研究对象与基本设定 我们希望学习一个能够“生成数据”的概率模型。假设我们有一个数据集 \(D\) ，每个样本是 \(n\) 维二值向量： \(x \in \{0,1\}^n\) 我们的目标是用一个参数化分布 \(p_\theta(x)\) 去逼近真实数据分布 \(p_{\text{data}}(x)\) ，并最终能够： 密度估计 ：给定 \(x\) 计算 \(p_\theta(x)\) 或 \(\log p_\theta(x)\) 采样生成 ：从 \(p_\theta(x)\) 采样得到新的 \(x\) 表示：链式法则与自回归分解 链式法则分解联合分布 任意联合分布都可用概率链式法则分解为条件概率的乘积： \[p(x) = \prod_{i=1}^{n} p(x_i \mid x_1, x_2, \dots, x_{i-1}) = \prod_{i=1}^{n} p(x_i \mid x_{<i})\] 其中： \(x_{<i} = [x_1, x_2, \dots, x_{i-1}]\) ，这意味着：只要我们能为每个维度 \(i\) 学好一个条件分布 \(p(x_i \mid...

背景 本文主要是《NICE: Nonlinear Independent Components Estimation》一文的介绍和实现。这篇文章也是glow这个模型的基础文章之一，可以说它就是glow的奠基石。 艰难的分布 众所周知，目前主流的生成模型包括VAE和GAN，但事实上除了这两个之外，还有基于flow的模型（flow可以直接翻译为“流”，它的概念我们后面再介绍）。事实上flow的历史和VAE、GAN它们一样悠久，但是flow却鲜为人知。在我看来，大概原因是flow找不到像GAN一样的诸如“造假者鉴别者”的直观解释吧，因为flow整体偏数学化，加上早期效果没有特别好但计算量又特别大，所以很难让人提起兴趣来。不过现在看来，OpenAI的这个好得让人惊叹的、基于flow的glow模型，估...

💡 原本随机采样的DDPM模型中，也隐含了一个确定性的采样过程DDIM，它的连续极限也是一个ODE。 细想上述过程，可以发现不管是“DDPM→DDIM”还是“SDE→ODE”，都是从随机采样模型过渡到确定性模型，而如果我们一开始的目标就是ODE，那么该过程未免显得有点“迂回”了。在本文中，笔者尝试给出ODE扩散模型的直接推导，并揭示了它与雅可比行列式、热传导方程等内容的联系。 Rectified Flow 理论推导 微分方程 像GAN这样的生成模型，它本质上是希望找到一个确定性变换，能将从简单分布（如标准正态分布）采样出来的随机变量，变换为特定数据分布的样本。flow模型也是生成模型之一，它的思路是反过来，先找到一个能将数据分布变换简单分布的可逆变换，再求解相应的逆变换来得到一个生成模型。 ...

简介 之前的很多方法都是用RNN的结构去构建时序上的依赖关系，但是RNN的结构的缺点是不能并行操作，且存在梯度消失的现象。所以本文就是将之前的RNN的结构改为Transfomer的形式。延续了之前TRN的整个网络的框架，也是结合了对未来帧的预测与历史帧的表示相结合来对当前的动作进行预测。 方法 整个网络框架如上图所示， Encoder就是利用transfomer对longrange的历史和目前帧进行特征表示，其中要说明的一个点就是，这里的特征空间包含T个历史特征，当前窗口的特征以及一个task token，这个task token的作用可以从下图看出来 这幅图对比的是输入进classifier的特征与网络输入的特征的相似性，可以看出w/o task token 对应的是当前t=0时刻的特征，...

正则化 正则化是一个通用的算法和思想，所以会产生过拟合现象的算法都可以使用正则化来避免过拟合。 在经验风险最小化的基础上（也就是训练误差最小化），尽可能采用简单的模型，可以有效提高泛化预测精度。如果模型过于复杂，变量值稍微有点变动，就会引起预测精度问题。正则化之所以有效，就是因为其降低了特征的权重，使得模型更为简单。 正则化一般会采用 L1 范式或者 L2 范式，其形式分别为 [Math] 和 [Math] 。 L1正则化 LASSO 回归，相当于为模型添加了这样一个先验知识： w 服从零均值拉普拉斯分布。 首先看看拉普拉斯分布长什么样子： [公式] 由于引入了先验知识，所以似然函数这样写： [公式] 取 log 再取负，得到目标函数： [公式] 等价于原始损失函数的后面加上了 L1 正则，...

Kernel Logistic Regression 介绍如何将Kernel Trick引入到Logistic Regression，以及LR与SVM的结合 SVM与正则化 首先回顾SoftMargin SVM的原始问题: [公式] 其中 ξ_n 是训练数据违反边界的多少，没有违反的话， ξ_n=0 ，反之 ξ_n0 ，换句话说，目标函数的第二项就可以表示模型的损失。现在换一种方式来写，将二者结合起来: ξ_n=max(1−y_n(w^Tz^n+b),0) ，这一个等式就代表了上面的约束条件，这样上述问题，就与下面的无约束问题等价 [公式] 这种形式与之前的L2 正则项很类似: [公式] 在L2中，通过最小化 E_{in} 的同时控制 w 的大小，防止模型过度复杂。从正则化的角度来看的话，S...

EM算法也称期望最大化（ExpectationMaximum,简称EM）算法，它是一个基础算法，是很多机器学习领域算法的基础，比如隐式马尔科夫算法（HMM）， LDA主题模型的变分推断等等。本文就对EM算法的原理做一个总结。 EM算法要解决的问题 我们经常会从样本观察数据中，找出样本的模型参数。 最常用的方法就是极大化模型分布的对数似然函数。 但是在一些情况下，我们得到的观察数据有未观察到的隐含数据，此时我们未知的有隐含数据和模型参数，因而无法直接用极大化对数似然函数得到模型分布的参数。怎么办呢？这就是EM算法可以派上用场的地方了。 EM算法解决这个的思路是使用启发式的迭代方法，既然我们无法直接求出模型分布参数，那么我们可以先猜想隐含数据（EM算法的E步），接着基于观察数据和猜测的隐含数据一...

是什么 过拟合（overfitting）是指在模型参数拟合过程中的问题，由于训练数据包含抽样误差，训练时，复杂的模型将抽样误差也考虑在内，将抽样误差也进行了很好的拟合。 具体表现就是最终模型在训练集上效果好；在测试集上效果差。模型泛化能力弱。 为什么 为什么要解决过拟合现象？这是因为我们拟合的模型一般是用来预测未知的结果（不在训练集内），过拟合虽然在训练集上效果好，但是在实际使用时（测试集）效果差。同时，在很多问题上，我们无法穷尽所有状态，不可能将所有情况都包含在训练集上。所以，必须要解决过拟合问题。 为什么在机器学习中比较常见？这是因为机器学习算法为了满足尽可能复杂的任务，其模型的拟合能力一般远远高于问题复杂度，也就是说，机器学习算法有「拟合出正确规则的前提下，进一步拟合噪声」的能力。 而...