INCOMING TRANSMISSION

76. 最小覆盖子串 题目 给定两个字符串 s 和 t ，长度分别是 m 和 n ，返回 s 中的 最短窗口 子串 ，使得该子串包含 t 中的每一个字符（ 包括重复字符 ）。如果没有这样的子串，返回空字符串 "" 。 测试用例保证答案唯一。 示例 1： 输入：s = "ADOBECODEBANC", t = "ABC" 输出："BANC" 解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。 示例 2： 输入：s = "a", t = "a" 输出："a" 解释：整个字符串 s 是最小覆盖子串。 示例 3: 输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中， 因此没有符合条件的子字符串，返回空字符串。 提示： m == s.length n == t.length 1 <= m, n <= 10 5 s 和 t 由英文字母组成 题解 这是一个经典的 滑动窗口 (Sliding Window) 问题 我们需要维护一个动态的窗口 [left, right] ： 右移扩大 ：不断移动...

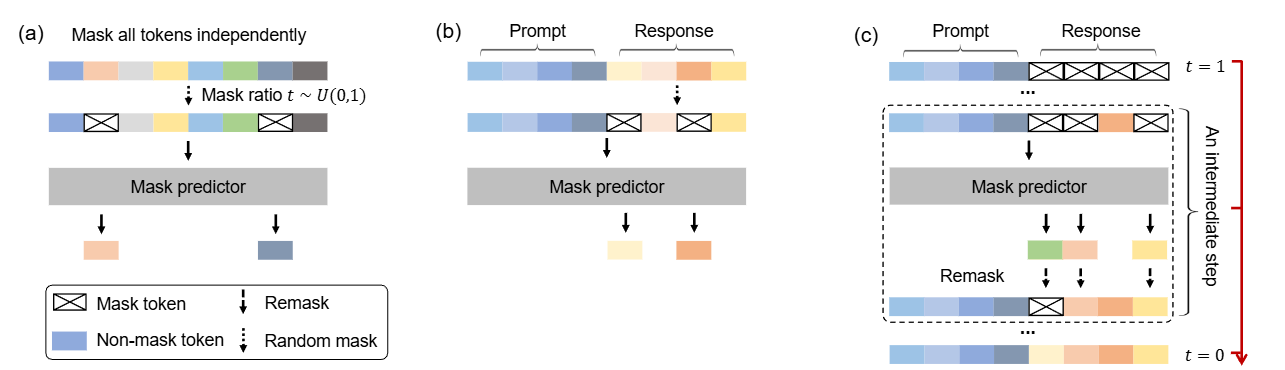
这是一篇尝试改变LLM「范式」的文章：当前主流的LLM架构都是「自回归」的，通俗地理解就是必须「从左到右依次生成」。这篇文章挑战了这一范式，探索扩散模型在 LLMs 上的可行性，通过 随机掩码 - 预测 的逆向思维，让模型学会「全局思考」。 论文： [2502.09992] Large Language Diffusion Models 背景 主流大语言模型架构：自回归模型 (Autoregressive LLMs) 过去几年， 自回归模型（Autoregressive Models, ARMs）一直是大语言模型(LLM)的主流架构​。典型的自回归语言模型以Transformer解码器为基础，按照从左到右 的顺序依次预测下一个词元(token)。 形式化地，自回归模型将一个长度为 \(N\) 的文本序列 \(X=(x_1, x_2, ..., x_N)\) 的概率分解为各位置的条件概率连乘积​： \[P_{\theta}(x_1, x_2, \dots, x_N) = \prod_{i=1}^{N} P_{\theta}(x_i \mid x_1, x_2, \dots,...

引言 Diffusion模型近年来在图像生成这一连续域任务中取得了显著成果，展现出强大的生成能力。然而，在文本生成这一离散域任务中整体效果仍不尽如人意，未能在该领域引起广泛关注。 去年，一篇研究离散扩散模型在文本生成的文章《Discrete Diffusion Modeling by Estimating the Ratios of the Data Distribution》获得ICML 2024的Best Paper，引发了学术界的广泛兴趣，也激发了新一轮的研究热潮。随后在2025年，越来越多高校和企业也开始积极探索基于Diffusion的文本生成方法。其中，近期备受关注的Block Diffusion也成功入选ICLR oral，进一步推动了该方向的发展。...

💡 扩散模型：通过加噪的方式去学习原始数据的分布， 从学到的分布中去生成样本 DDPM 关键点： 1. 正向加噪是离散时间马尔可夫链：从 \(x_0\) 逐步加噪得到 \(x_1,x_2,...,x_T\) ；在合适的噪声调度与足够大的 \(T\) 下， \(x_T\) 近似服从 \( N(0,I) \) 的各向同性高斯。 2. 每一步噪声方差 \(β_t\) 满足 \(0<β_t<1\) ，通常随 \(t\) 增大；因此 \(q(x_t|x_{t-1}) \) 的均值缩放系数 \(\sqrt{1-β_t} \) 逐渐减小。 3. 训练通过最大化对数似然的变分下界（ELBO）来学习反向过程 \( p_θ(x_{t-1}|x_t)\) ，并将其参数化为高斯分布（神经网络预测均值/噪声或 score）。 4. 将目标写成 score/DSM 形式时，loss 的权重与对应噪声层的方差尺度（如 \(1-\bar{α}_t\) 或相关量）有关；采样通常是按学习到的反向转移逐步生成（祖先采样），与经典 Langevin MCMC 更新形式不同，但可在 SDE 视角下统一理解。...

基于文章 《Elucidating the Design Space of Diffusion-Based Generative Models》 来统一扩散模型框架 通用扩散模型框架推导 加噪公式 Flow Matching的一步加噪公式 \[\mathbf{x}_t=(1-t)\mathbf{x}_0+t\varepsilon\] 写成概率分布形式： \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;(1-t)\mathbf{x}_0,t^2\mathbf{I})\] Score Matching的一步加噪公式 \[\mathbf{x}_t=\mathbf{x}_0+\sigma_t\varepsilon \] 写成概率分布形式： \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;\mathbf{x}_0,\sigma_t^2\mathbf{I})\] DDPM/DDIM的一步加噪公式...

💡 原本随机采样的DDPM模型中，也隐含了一个确定性的采样过程DDIM，它的连续极限也是一个ODE。 细想上述过程，可以发现不管是“DDPM→DDIM”还是“SDE→ODE”，都是从随机采样模型过渡到确定性模型，而如果我们一开始的目标就是ODE，那么该过程未免显得有点“迂回”了。在本文中，笔者尝试给出ODE扩散模型的直接推导，并揭示了它与雅可比行列式、热传导方程等内容的联系。 Rectified Flow 理论推导 微分方程 像GAN这样的生成模型，它本质上是希望找到一个确定性变换，能将从简单分布（如标准正态分布）采样出来的随机变量，变换为特定数据分布的样本。flow模型也是生成模型之一，它的思路是反过来，先找到一个能将数据分布变换简单分布的可逆变换，再求解相应的逆变换来得到一个生成模型。 ...

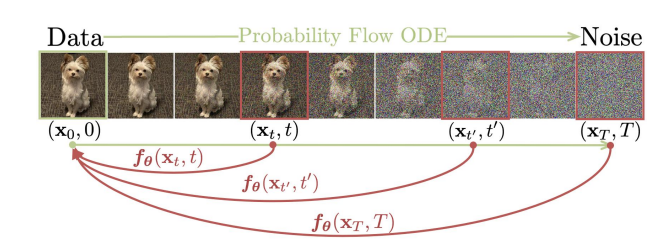
DDPM 有一个非常明显的问题：采样过程很慢。因为 DDPM 的反向过程利用了马尔可夫假设，所以每次都必须在相邻的时间步之间进行去噪，而不能跳过中间步骤。原始论文使用了 1000 个时间步，所以我们在采样时也需要循环 1000 次去噪过程，这个过程是非常慢的。 为了加速 DDPM 的采样过程，DDIM 在不利用马尔可夫假设的情况下推导出了 diffusion 的反向过程，最终可以实现仅采样 20～100 步的情况下达到和 DDPM 采样 1000 步相近的生成效果，也就是提速 10～50 倍。这篇文章将对 DDIM 的理论进行讲解，并实现 DDIM 采样的代码。 DDPM 的反向过程 首先我们回顾一下 DDPM 反向过程的推导，为了推导出 [Math] 这个条件概率分布，DDPM 利用贝叶斯...

这是OpenCompass的offitial ranking 榜单 🔖 https://rank.opencompass.org.cn/home MMBench 鉴于现行评测方式所存在的问题，我们重新定义了一套针对当前多模态大模型的评测流程——MMBench。其主要包含两个方面: 自上而下的能力维度设计，根据定义的能力维度构造了一个评测数据集 引入 ChatGPT，以及提出了 CircularEval 的评测方式，使得评测的结果更加稳定 Paper 链接: 🔖 https://arxiv.org/pdf/2307.06281 github： 数据集 数据集构造 主要目的是对模型的各种能力进行全方位的考察，所以我们自上而下定义了三级能力维度 (L1L3)， 第一级维度（L1）包含感知与推理两项...

Diffusion Models from SDE 连续扩散模型 (Continuous Diffusion Models) 将传统的离散时间扩散过程扩展到连续时间域,可以被视为一个随机过程，使用随机微分方程(SDE)来描述。其前向过程可以写成如下形式： [公式] 其中， f(x,t) 可以看成偏移系数， g(t) 可以看成是扩散系数， dw 是标准布朗运动。这个SDE 描述了数据在连续时间域内如何被噪声逐渐破坏。 这个随机过程的逆向过程存在（更准确的描述：下面的逆向时间SDE具有与正向过程SDE相同的联合分布）为 [公式] 前面我们得到了扩散过程的逆向过程可以用一个SDE描述(逆向随机过程),事实上，存在一个确定性过程 (用ODE描述)也是它的逆向过程 (更准确的描述：这个ODE过程的在任...

💡 Flowbased Models Normalizing Flow Normalizing Flow 是一种基于变换对概率分布进行建模的模型，其通过一系列离散且可逆的变换实现任意分布与先验分布（例如标准高斯分布）之间的相互转换。在 Normalizing Flow 训练完成后，就可以直接从高斯分布中进行采样，并通过逆变换得到原始分布中的样本，实现生成的过程。（有关 Normalizing Flow 的详细理论） 从这个角度看，Normalizing Flow 和 Diffusion Model 是有一些相通的，其做法的对比如下表所示。从表中可以看到，两者大致的过程是非常类似的，尽管依然有些地方不一样，但这两者应该可以通过一定的方法得到一个比较统一的表示。 Continuous Norma...

技术分析 从方法上来看，条件控制生成的方式分两种：事后修改（ClassifierGuidance）和事前训练（ClassifierFree）。 对于大多数人来说，一个SOTA级别的扩散模型训练成本太大了，而分类器（Classifier）的训练还能接受，所以就想着直接复用别人训练好的无条件扩散模型，用一个分类器来调整生成过程以实现控制生成，这就是事后修改的ClassifierGuidance方案；而对于“财大气粗”的Google、OpenAI等公司来说，它们不缺数据和算力，所以更倾向于往扩散模型的训练过程中就加入条件信号，达到更好的生成效果，这就是事前训练的ClassifierFree方案。 ClassifierGuidance方案最早出自《Diffusion Models Beat GANs...

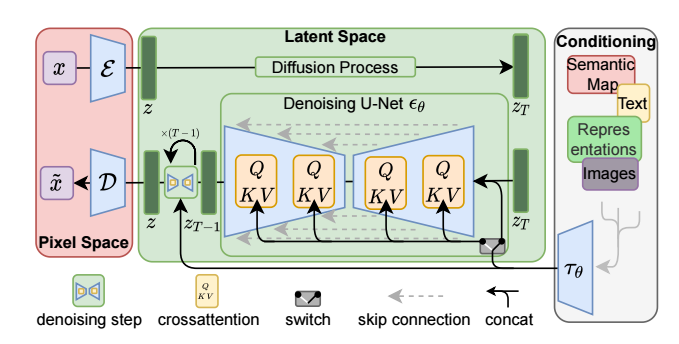
SD模型原理 SD是CompVis、Stability AI和LAION等公司研发的一个文生图模型，它的模型和代码是开源的，而且训练数据LAION5B也是开源的。SD在开源90天github仓库就收获了33K的stars，可见这个模型是多受欢迎。 SD是一个基于latent的扩散模型，它在UNet中引入text condition来实现基于文本生成图像。SD的核心来源于Latent Diffusion这个工作，常规的扩散模型是基于pixel的生成模型，而Latent Diffusion是基于latent的生成模型，它先采用一个autoencoder将图像压缩到latent空间，然后用扩散模型来生成图像的latents，最后送入autoencoder的decoder模块就可以得到生成的图像。 ...