INCOMING TRANSMISSION

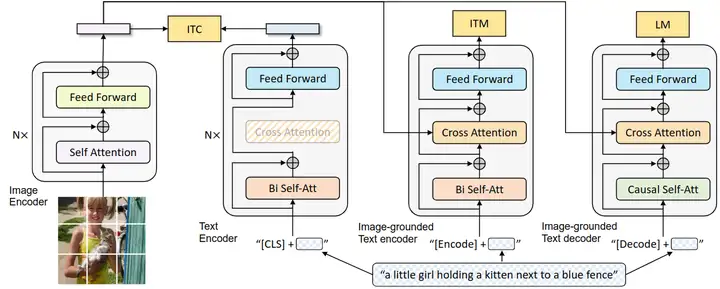
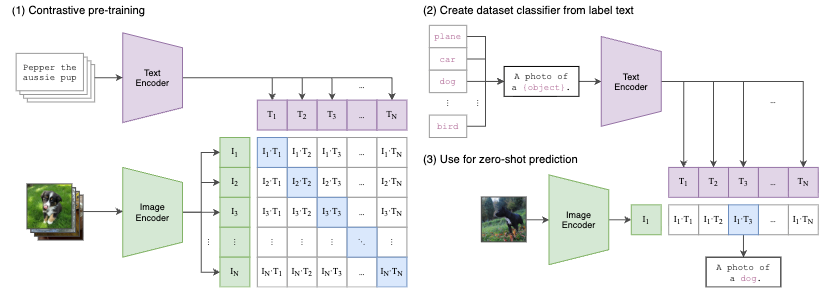
BLIP 论文名称 ：BLIP: Bootstrapping Language-Image Pre-training for Unified Vision-Language Understanding and Generation (ICML 2022) 论文地址： https://arxiv.org/pdf/2201.12086.pdf 代码地址： https://github.com/salesforce/BLIP 官方解读博客： https://blog.salesforceairesearch.com/blip-bootstrapping-language-image-pretraining/ 背景和动机 视觉语言训练 (Vision-Language Pre-training, VLP) 最近在各种多模态下游任务上取得了巨大的成功。然而，现有方法有两个主要限制： 模型层面： 大多数现有的预训练模型仅在基于理解的任务或者基于生成的任务方面表现出色，很少有可以兼顾的模型。比如，基于编码器的模型，像 CLIP，ALBEF 不能直接转移到文本生成任务...

CLIP算法原理 CLIP 不预先定义图像和文本标签类别，直接利用从互联网爬取的 400 million 个image-text pair 进行图文匹配任务的训练，并将其成功迁移应用于30个现存的计算机视觉分类。简单的说，CLIP 无需利用 ImageNet 的数据和标签进行训练，就可以达到 ResNet50 在 ImageNet数据集上有监督训练的结果，所以叫做 Zero-shot。 CLIP（contrastive language-image pre-training）主要的贡献就是 利用无监督的文本信息，作为监督信号来学习视觉特征 。 CLIP 作者先是回顾了并总结了和上述相关的两条表征学习路线： 构建image和text的联系，比如利用已有的image-text pair数据集，从text中学习image的表征； 获取更多的数据（不要求高质量，也不要求full...

数组&链表&字符串 双指针 滑动窗口 哈希表 哈希表 栈&队列 单调队列 树与堆 图 数学 Math

128. 最长连续序列 题目 给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 1： 输入：nums = [100,4,200,1,3,2] 输出：4 解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。 示例 2： 输入：nums = [0,3,7,2,5,8,4,6,0,1] 输出：9 示例 3： 输入：nums = [1,0,1,2] 输出：3 提示： 0 <= nums.length <= 10 5 -10 9 <= nums[i] <= 10 9 题解 我们需要在 \(O(1)\) 的时间内查找某个数是否存在。因此，首先将数组中的所有元素放入一个 HashSet 中。这不仅能去重，还能支持快速查找。 避免冗余计算 (关键优化) 如果我们对集合中的每一个数都尝试去向后计数（例如，对于 x ，尝试找 x+1 , x+2 ...），最坏情况下的时间复杂度会退化到 \(O(n^2)\) 。 优化策略 ： 我们 只从序列的起点开始计数 。...

76. 最小覆盖子串 题目 给定两个字符串 s 和 t ，长度分别是 m 和 n ，返回 s 中的 最短窗口 子串 ，使得该子串包含 t 中的每一个字符（ 包括重复字符 ）。如果没有这样的子串，返回空字符串 "" 。 测试用例保证答案唯一。 示例 1： 输入：s = "ADOBECODEBANC", t = "ABC" 输出："BANC" 解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。 示例 2： 输入：s = "a", t = "a" 输出："a" 解释：整个字符串 s 是最小覆盖子串。 示例 3: 输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中， 因此没有符合条件的子字符串，返回空字符串。 提示： m == s.length n == t.length 1 <= m, n <= 10 5 s 和 t 由英文字母组成 题解 这是一个经典的 滑动窗口 (Sliding Window) 问题 我们需要维护一个动态的窗口 [left, right] ： 右移扩大 ：不断移动...

简介 生成树（spanning tree） 在图论中，无向图 G=(V,E) 的生成树（spanning tree)是具有G的全部顶点，但边数最少的联通子图。假设G中一共有n个顶点，一颗生成树满足下列条件： （1）n个顶点； （2）n1条边； （3）n个顶点联通； （4）一个图的生成树可能有多个。最小生成树（minimum spanning tree， MST）/最小生成森林：联通加权无向图中边缘权重加和最小的生成树。给定无向图 G=(V,E) ， (u,v) 代表顶点 u 与顶点 v 的边， w(u,v) 代表此边的权重，若存在生成树T使得： [公式] 最小，则 T 为 G 的最小生成树。对于非连通无向图来说，它的每一连通分量同样有最小生成树，它们的并被称为最小生成森林。最小生成树除了继承...

给一个无向图，判断其是否为一棵树。如果是树的话，所有的节点必须是连接的，也就是说必须是连通图，而且不能有环，所以就变成了验证是否是连通图和是否含有环。 [代码]

题目 中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。 例如， [2,3,4] 的中位数是 3 [2,3] 的中位数是 (2 + 3) / 2 = 2.5 设计一个支持以下两种操作的数据结构： void addNum(int num) 从数据流中添加一个整数到数据结构中。 double findMedian() 返回目前所有元素的中位数。 示例： addNum(1) addNum(2) findMedian() 1.5 addNum(3) findMedian() 2 题解 维护两个堆：大顶堆和小顶堆。并且需满足如下条件： 小顶堆的所有元素都大于等于大顶堆的所有元素。 大顶堆中的元素数量大于等于小顶堆中的元素数量。 大顶堆对应排序后的列表的左半部分；小顶堆对应排序...

[代码] 自己实现小顶堆 [代码] 变态的需求来了：给出N长的序列，求出BtmK小的元素，即使用大顶堆。 概括一种最简单的： 将push(e)改为push(e)、pop(e)改为pop(e)。 也就是说，在存入堆、从堆中取出的时候，都用相反数，而其他逻辑与TopK完全相同，看代码： [代码] 自己实现大顶堆 [代码]

二叉树结构 [代码] 递归 时间复杂度：O(n)，n为节点数，访问每个节点恰好一次。 空间复杂度：空间复杂度：O(h)，h为树的高度。最坏情况下需要空间O(n)，平均情况为O(logn) 递归1: 二叉树遍历最易理解和实现版本 [代码] 递归2: 通用模板 可以适应不同的题目，添加参数、增加返回条件、修改进入递归条件、自定义返回值 [代码] 迭代 时间复杂度：O(n)，n为节点数，访问每个节点恰好一次。 空间复杂度：O(h)，h为树的高度。取决于树的结构，最坏情况存储整棵树，即O(n) 迭代1: 前序遍历最常用模板（后序同样可以用） [代码] 迭代2: 前、中、后序遍历通用模板（只需一个栈的空间） [代码] 迭代3：标记法迭代（需要双倍的空间来存储访问状态） 前、中、后、层序通用模板，只需改...