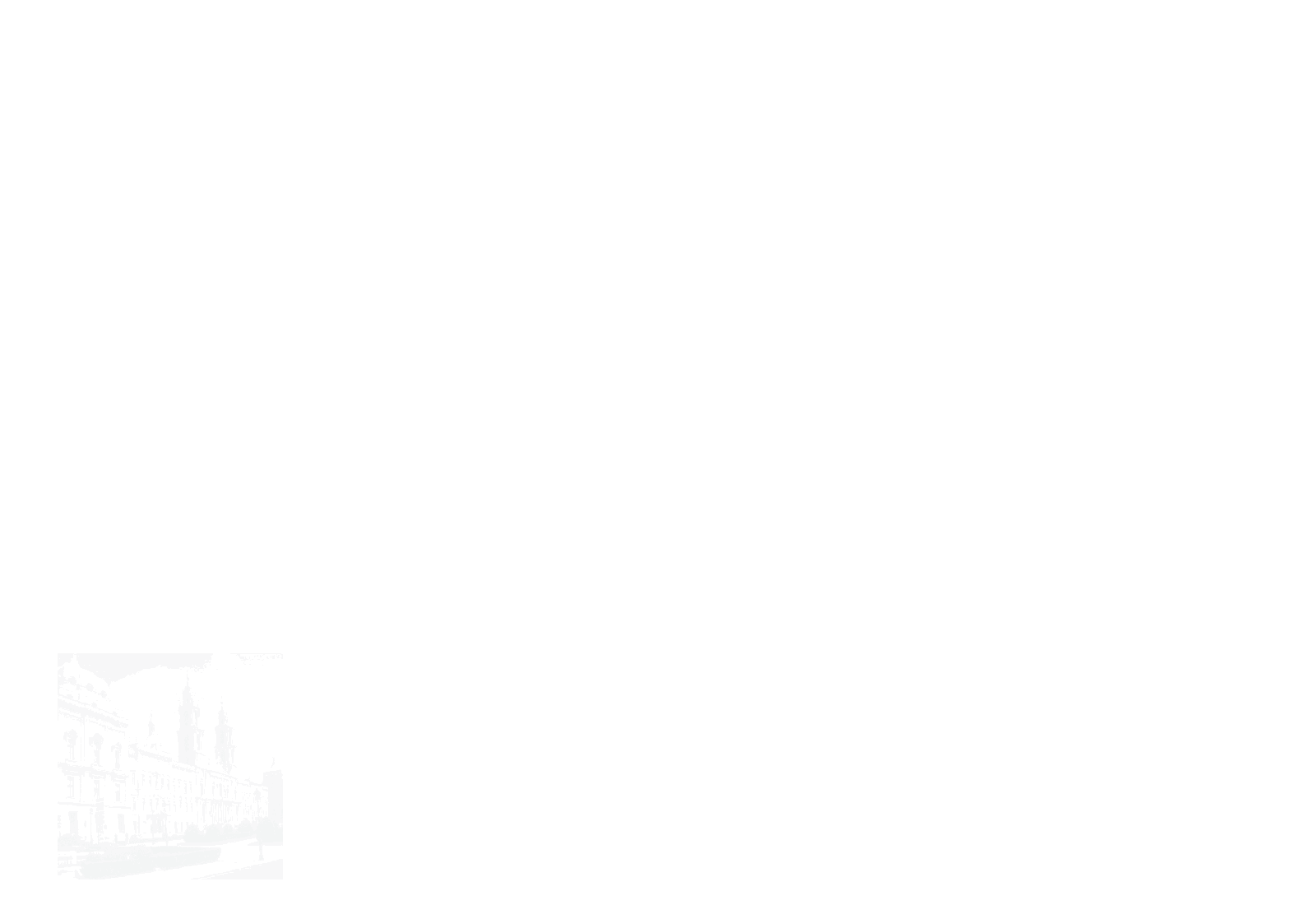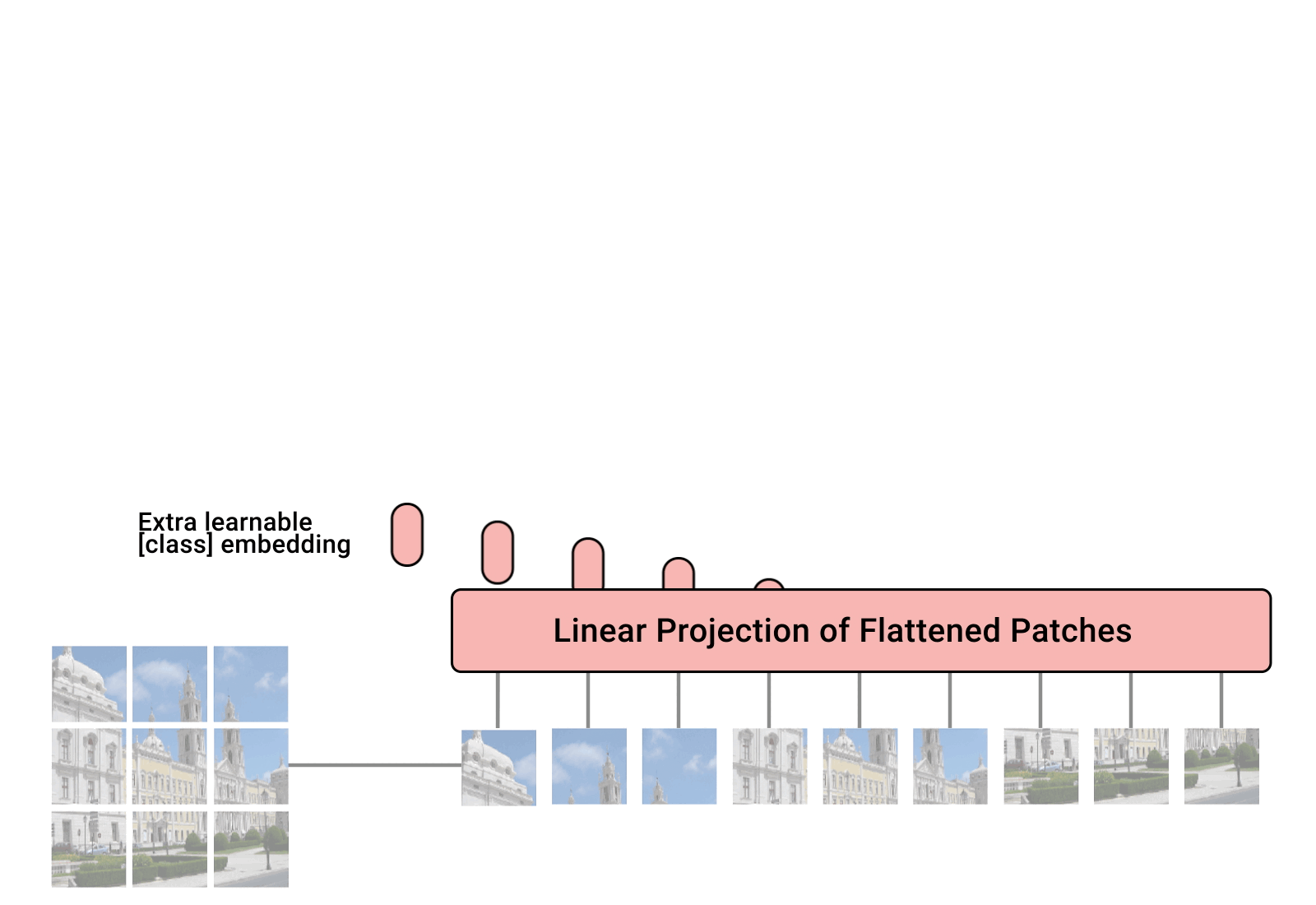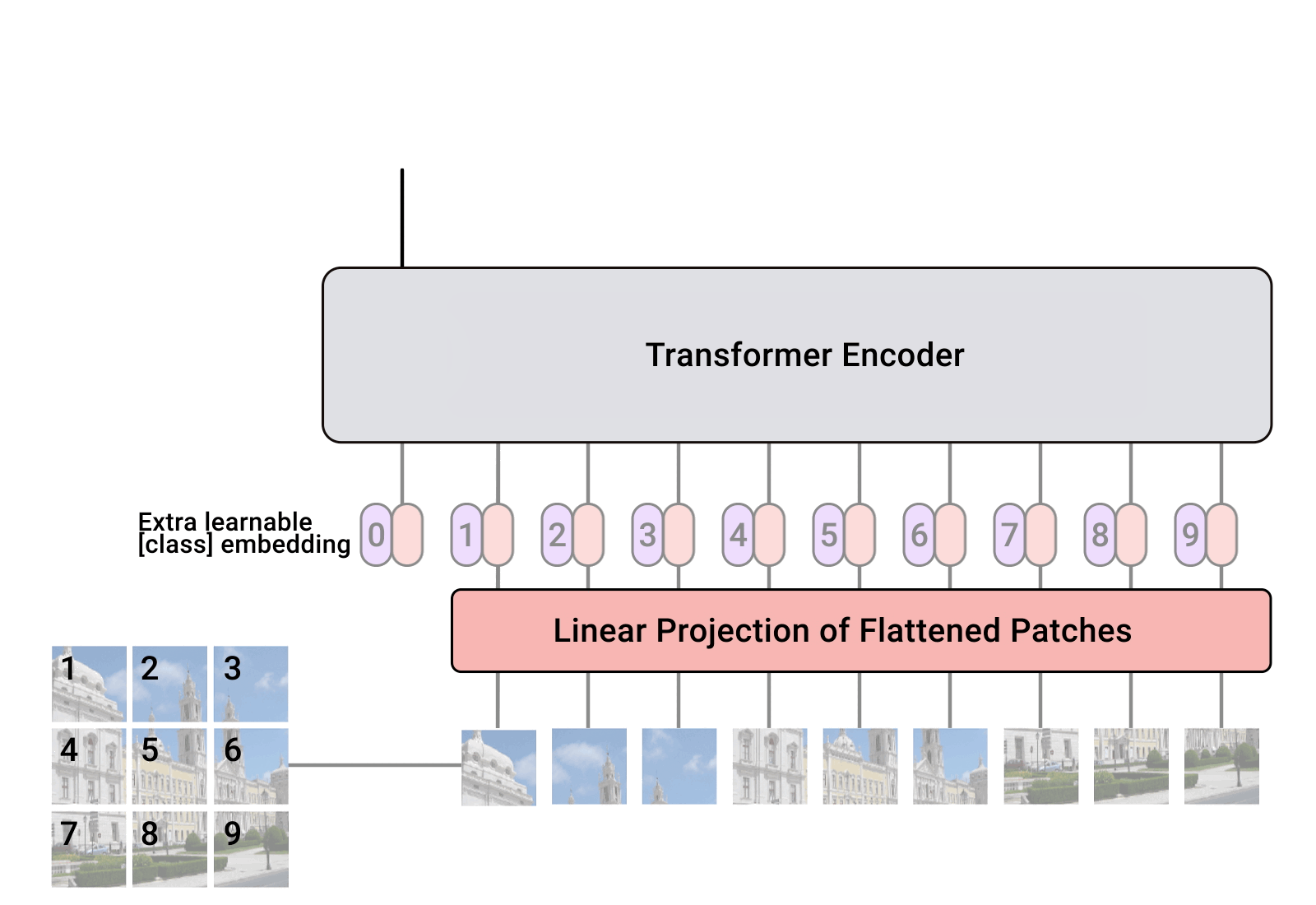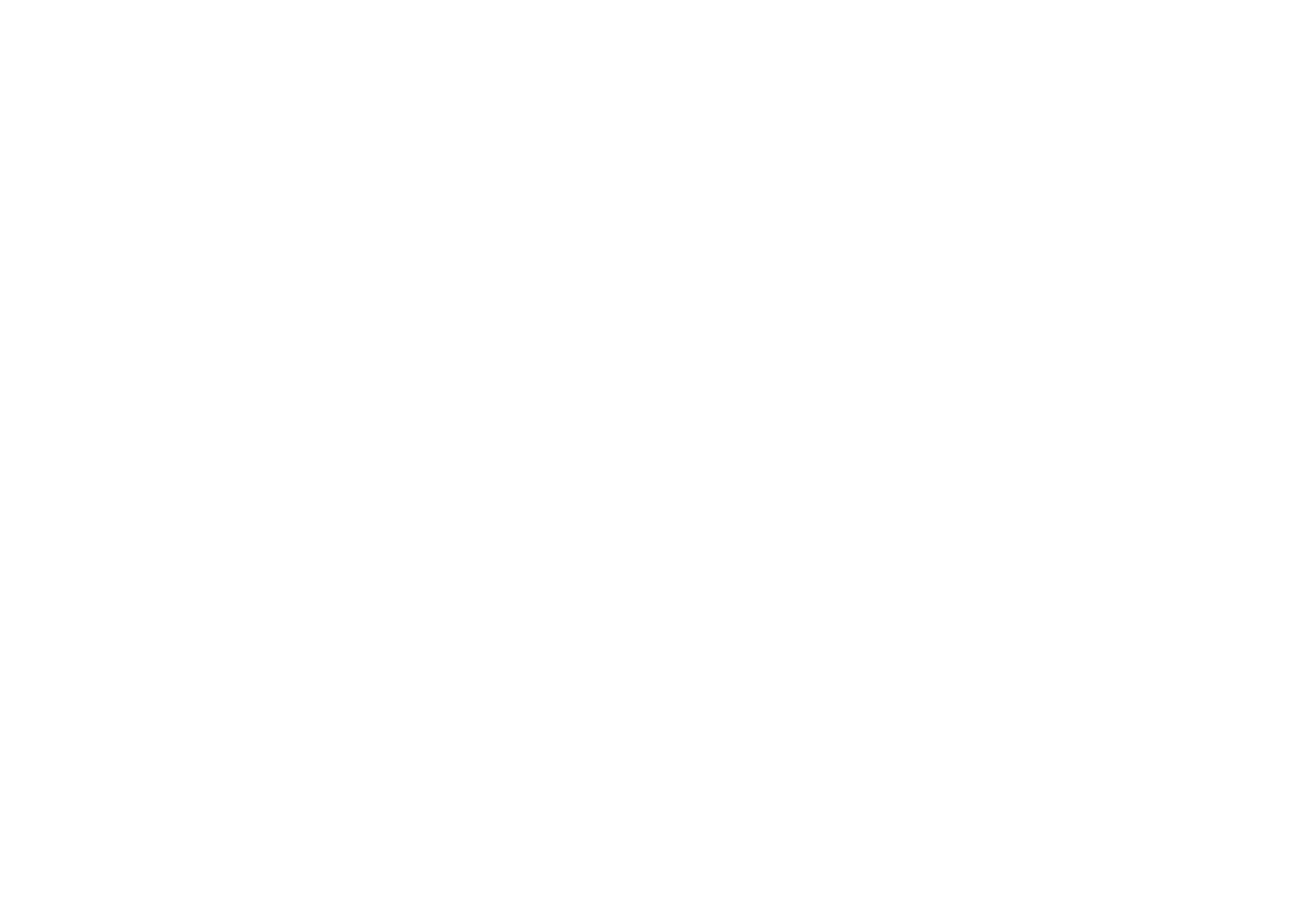INCOMING TRANSMISSION

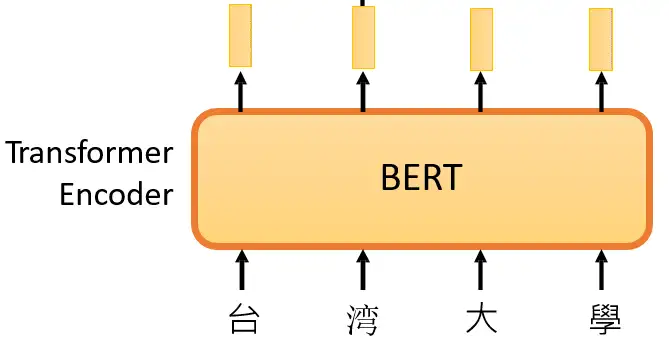
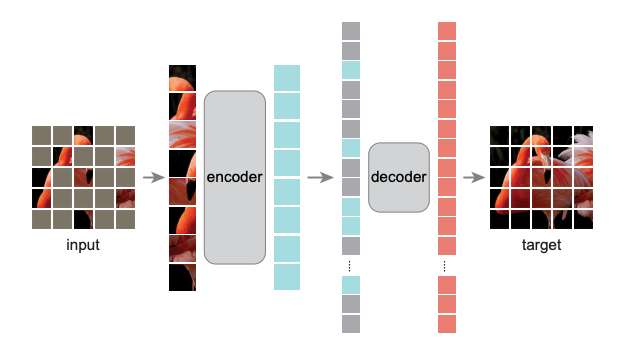
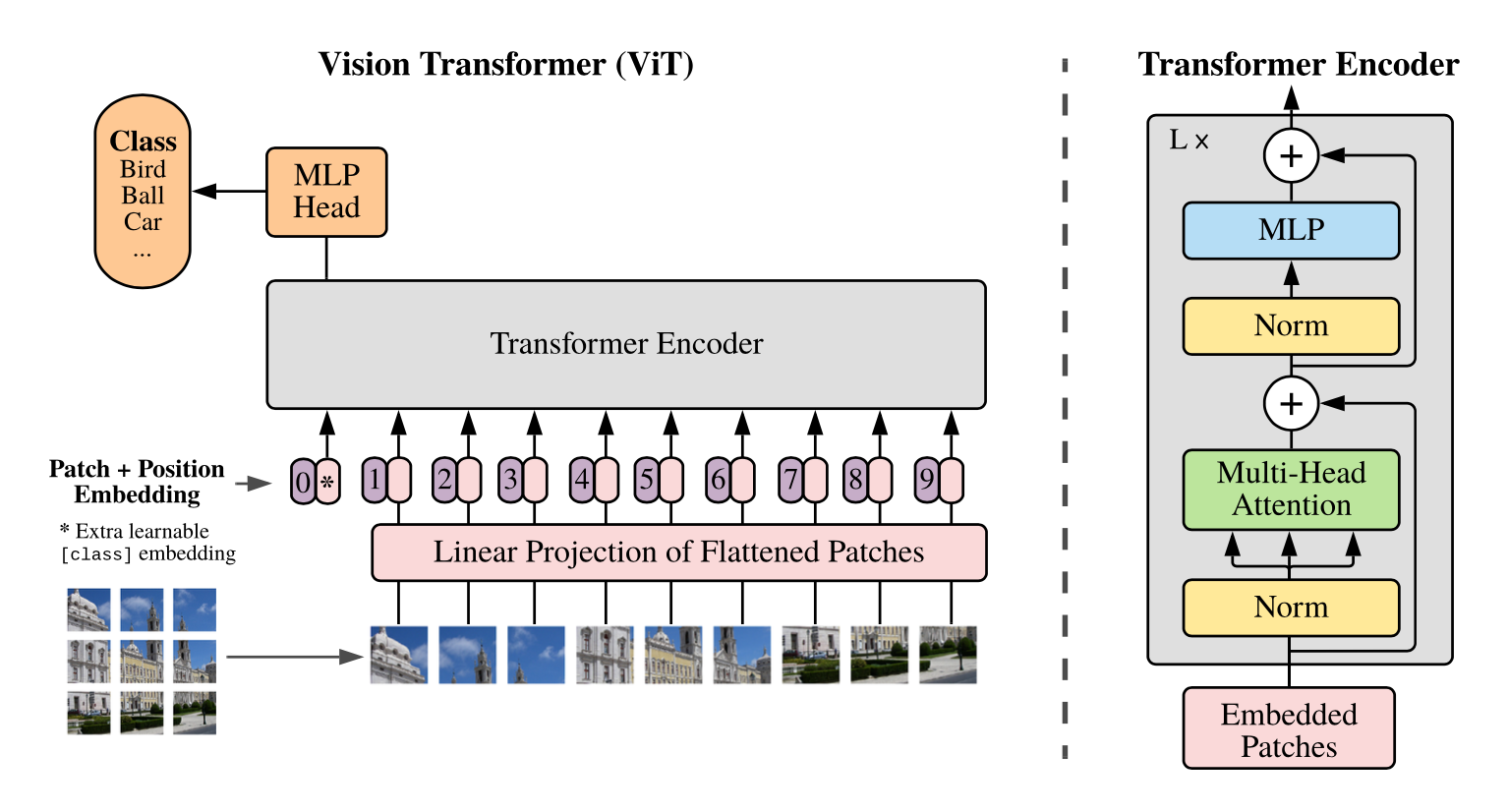
BERT 方法回顾 在 大规模预训练模型BERT 里面我们介绍了 BERT 的自监督预训练的方法，BERT 可以做的事情也就是Transformer 的 Encoder 可以做的事情，就是输入一排向量，输出另外一排向量，输入和输出的维度是一致的。那么不仅仅是一句话可以看做是一个sequence，一段语音也可以看做是一个sequence，甚至一个image也可以看做是一个sequence。所以BERT其实不仅可以用在NLP上，还可以用在CV里面。所以BERT其实输入的是一段文字，如下图所示。 BERT的架构就是Transformer 的 Encoder 接下来要做的事情是把这段输入文字里面的一部分随机盖住。随机盖住有 2 种，一种是直接用一个Mask 把要盖住的token (对中文来说就是一个字)给Mask掉，具体是换成一个 特殊的字符 。另一种做法是把这个token替换成一个随机的token。 把这段输入文字里面的一部分随机盖住 具体BERT详情可以参考： 大规模预训练模型BERT BERT 可以直接用在视觉任务上吗？ 上面的 BERT 都是在 NLP 任务上使用，因为 NLP...

Self-Supervised Learning ，又称为自监督学习，我们知道一般机器学习分为有监督学习，无监督学习和强化学习。 而 Self-Supervised Learning 是无监督学习里面的一种，主要是希望能够学习到一种 通用的特征表达 用于 下游任务 (Downstream Tasks) 。 其主要的方式就是通过自己监督自己。作为代表作的 kaiming 的 MoCo 引发一波热议， Yann Lecun也在 AAAI 上讲 Self-Supervised Learning 是未来的大势所趋。所以在这个系列中，我会系统地解读 Self-Supervised Learning 的经典工作。 本文主要介绍 Self-Supervised Learning 在 NLP领域 的经典工作：BERT模型的原理及其变体。 本文来自台湾大学李宏毅老师PPT： https://speech.ee.ntu.edu.tw/~hylee/ml/ml2021-course-data/bert_v8.pdf 芝麻街 在介绍 Self-Supervised Learning...

数组&链表&字符串 双指针 滑动窗口 哈希表 哈希表 栈&队列 单调队列 树与堆 图 数学 Math

导言 自监督学习（Self-Supervised Learning）能利用大量无标注的数据进行表征学习，然后在特定下游任务上对参数进行微调。通过这样的方式，能够在较少有标注数据上取得优于有监督学习方法的精度。近年来，自监督学习受到了越来越多的关注，如Yann Lecun也在 AAAI 上讲 Self-Supervised Learning 是未来的大势所趋。在CV领域涌现了如SwAV、MOCO、DINO、MoBY等一系列工作。MAE是kaiming继MOCO之后在自监督学习领域的又一力作。首先，本文会对MAE进行解读，然后基于EasyCV库的精度复现过程及其中遇到的一些问题作出解答。 概述 MAE的做法很简单：随机mask掉图片中的一些patch，然后通过模型去重建这些丢失的区域。包括两个核心的设计：1.非对称编码-解码结构 2.用较高的掩码率（75%）。通过这两个设计MAE在预训练过程中可以取得3倍以上的训练速度和更高的精度，如ViT-Huge能够通过ImageNet-1K数据上取得87.8%的准确率。 模型拆解...

概述 在计算机视觉领域（CV），对视觉特征的理解CNN是长期处于主导地位的。而在NLP领域，Transformer框架的巨大成功，也激发了不少研究者探索将Transformer用于计算机视觉任务。ViT（Vision Transformer）的出现标志着在CV领域Transformer架构迈出了重要的一步。尤其在当前结合LLM的多模态探索上（MM-LLM），都是以LLM大语言模型为骨干架构的模型，多种模态的信息需要先做token化处理，再输入到LLM模型。ViT天然具有序列化特征的建模能力，自然在MM-LLM探索中大放异彩~ ViT在多模态模型中的角色类似于自然语言建模中的Tokenizer组件，对图像进行视觉特征编码，产出图像的序列特征。只不过ViT的编码过程本身也是采用了Transformer的模型结构。 本文主要结合几篇paper和源码讲讲ViT和针对ViT的一些优化方法~ ViT（Vision Transformer）...

ViT（vision transformer）是Google在2020年提出的直接将transformer应用在图像分类的模型，后面很多的工作都是基于ViT进行改进的。ViT的思路很简单：直接把图像分成固定大小的patchs，然后通过线性变换得到patch embedding，这就类比NLP的words和word embedding，由于transformer的输入就是a sequence of token embeddings，所以将图像的patch embeddings送入transformer后就能够进行特征提取从而分类了。ViT模型原理如下图所示，其实ViT模型只是用了transformer的Encoder来提取特征（原始的transformer还有decoder部分，用于实现sequence to sequence，比如机器翻译）。下面将分别对各个部分做详细的介绍。 Patch Embedding 对于ViT来说，首先要将原始的2-D图像转换成一系列1-D的patch embeddings，这就好似NLP中的word embedding。输入的2-D图像记为 \(x\in...

这是一篇尝试改变LLM「范式」的文章：当前主流的LLM架构都是「自回归」的，通俗地理解就是必须「从左到右依次生成」。这篇文章挑战了这一范式，探索扩散模型在 LLMs 上的可行性，通过 随机掩码 - 预测 的逆向思维，让模型学会「全局思考」。 论文： [2502.09992] Large Language Diffusion Models 背景 主流大语言模型架构：自回归模型 (Autoregressive LLMs) 过去几年， 自回归模型（Autoregressive Models, ARMs）一直是大语言模型(LLM)的主流架构​。典型的自回归语言模型以Transformer解码器为基础，按照从左到右 的顺序依次预测下一个词元(token)。 形式化地，自回归模型将一个长度为 \(N\) 的文本序列 \(X=(x_1, x_2, ..., x_N)\) 的概率分解为各位置的条件概率连乘积​： \[P_{\theta}(x_1, x_2, \dots, x_N) = \prod_{i=1}^{N} P_{\theta}(x_i \mid x_1, x_2, \dots,...

引言 Diffusion模型近年来在图像生成这一连续域任务中取得了显著成果，展现出强大的生成能力。然而，在文本生成这一离散域任务中整体效果仍不尽如人意，未能在该领域引起广泛关注。 去年，一篇研究离散扩散模型在文本生成的文章《Discrete Diffusion Modeling by Estimating the Ratios of the Data Distribution》获得ICML 2024的Best Paper，引发了学术界的广泛兴趣，也激发了新一轮的研究热潮。随后在2025年，越来越多高校和企业也开始积极探索基于Diffusion的文本生成方法。其中，近期备受关注的Block Diffusion也成功入选ICLR oral，进一步推动了该方向的发展。...

💡 扩散模型：通过加噪的方式去学习原始数据的分布， 从学到的分布中去生成样本 DDPM 关键点： 1. 正向加噪是离散时间马尔可夫链：从 \(x_0\) 逐步加噪得到 \(x_1,x_2,...,x_T\) ；在合适的噪声调度与足够大的 \(T\) 下， \(x_T\) 近似服从 \( N(0,I) \) 的各向同性高斯。 2. 每一步噪声方差 \(β_t\) 满足 \(0<β_t<1\) ，通常随 \(t\) 增大；因此 \(q(x_t|x_{t-1}) \) 的均值缩放系数 \(\sqrt{1-β_t} \) 逐渐减小。 3. 训练通过最大化对数似然的变分下界（ELBO）来学习反向过程 \( p_θ(x_{t-1}|x_t)\) ，并将其参数化为高斯分布（神经网络预测均值/噪声或 score）。 4. 将目标写成 score/DSM 形式时，loss 的权重与对应噪声层的方差尺度（如 \(1-\bar{α}_t\) 或相关量）有关；采样通常是按学习到的反向转移逐步生成（祖先采样），与经典 Langevin MCMC 更新形式不同，但可在 SDE 视角下统一理解。...

基于文章 《Elucidating the Design Space of Diffusion-Based Generative Models》 来统一扩散模型框架 通用扩散模型框架推导 加噪公式 Flow Matching的一步加噪公式 \[\mathbf{x}_t=(1-t)\mathbf{x}_0+t\varepsilon\] 写成概率分布形式： \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;(1-t)\mathbf{x}_0,t^2\mathbf{I})\] Score Matching的一步加噪公式 \[\mathbf{x}_t=\mathbf{x}_0+\sigma_t\varepsilon \] 写成概率分布形式： \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;\mathbf{x}_0,\sigma_t^2\mathbf{I})\] DDPM/DDIM的一步加噪公式...