INCOMING TRANSMISSION

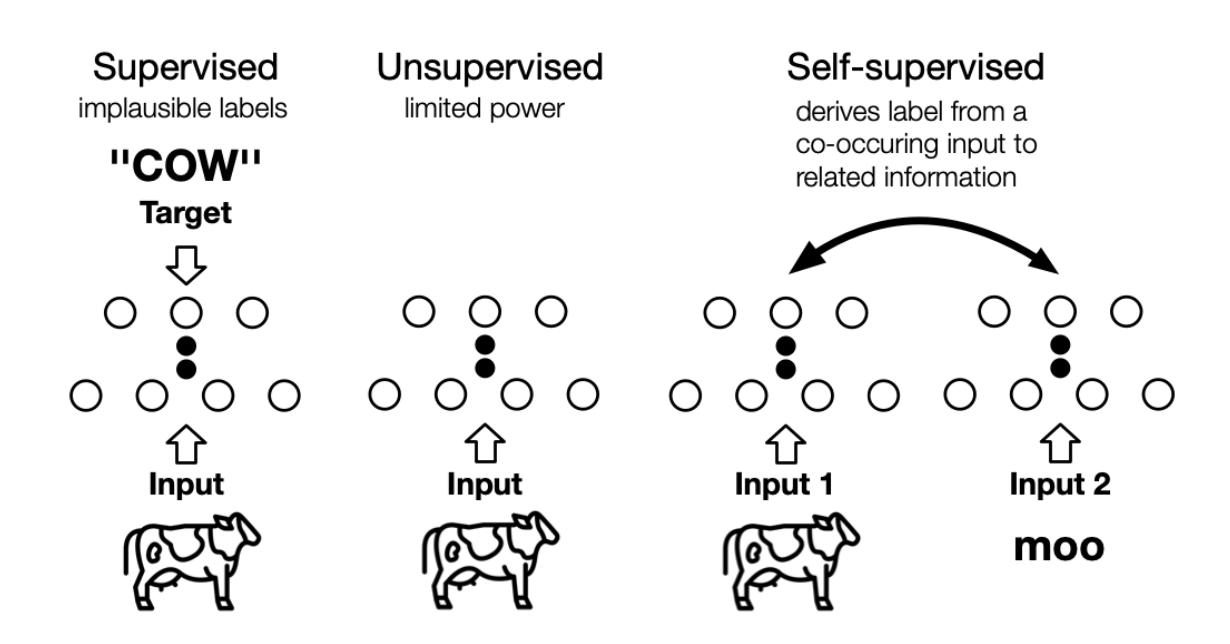
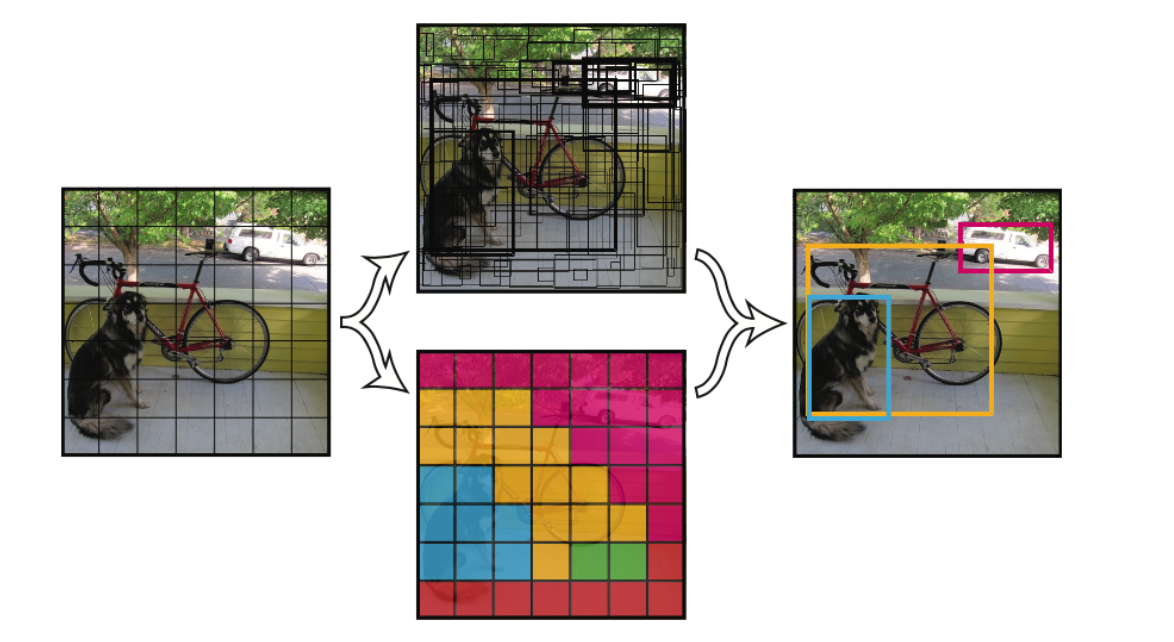
the machine predicts any parts of its input for any observed part 这是LeCun在AAAI 2020上对自监督学习的定义，再结合传统的自监督学习定义，可以总结如下两点特征： 通过“半自动”过程从数据本身获取“标签”； 从“其他部分”预测部分数据。 个人理解， 其实任意挖掘对象之间联系、探索不同对象共同本质的方法，都或多或少算是自监督学习的思想 。 自监督学习与无监督学习的区别主要在于，无监督学习专注于检测特定的数据模式，如聚类、社区发现或异常检测，而自监督学习的目标是恢复（recovering），仍处于监督学习的范式中。上图展示了三者之间的区别， 自监督中的“related information” 可以来自其他模态、输入的其他部分以及输入的不同形式。 Self-Supervised...

1.深度学习偏置的作用？ 我们在学深度学习的时候，最早接触到的神经网络应该属于感知器（感知器本身就是一个很简单的神经网络，也许有人认为它不属于神经网络，当然认为它和神经网络长得像也行） 要想激活这个感知器，使得 y=1 ，就必须使 x_1w_1 + x_2w_2 +....+x_nw_n T （ T 为一个阈值），而 T 越大，想激活这个感知器的难度越大，人工选择一个阈值并不是一个好的方法，因为样本那么多，我不可能手动选择一个阈值，使得模型整体表现最佳，那么我们可以使得T变成可学习的，这样一来， T 会自动学习到一个数，使得模型的整体表现最佳。当把T移动到左边，它就成了偏置， x_1w_1 + x_2w_2 +....+x_nw_n T 0 xw +b 0 ，总之，偏置的大小控制着激活这个感...

一般来说，神经网络处理的东西都是连续的浮点数，标准的输出也是连续型的数字。但实际问题中，我们很多时候都需要一个离散的结果，比如分类问题中我们希望输出正确的类别，“类别”是离散的，“类别的概率”才是连续的；又比如我们很多任务的评测指标实际上都是离散的，比如分类问题的正确率和F1、机器翻译中的BLEU，等等。 还是以分类问题为例，常见的评测指标是正确率，而常见的损失函数是交叉熵。交叉熵的降低与正确率的提升确实会有一定的关联，但它们不是绝对的单调相关关系。换句话说，交叉熵下降了，正确率不一定上升。显然，如果能用正确率的相反数做损失函数，那是最理想的，但正确率是不可导的（涉及到 [Math] 等操作），所以没法直接用。 这时候一般有两种解决方案；一是动用强化学习，将正确率设为奖励函数，这是“用牛刀杀...

在正式介绍之前，先简单回顾一下现有的两大类方法。第一大类，也是从非Deep时代，乃至CV初期就被就被广泛使用的方法叫做image pyramid。在image pyramid中，我们直接对图像进行不同尺度的缩放，然后将这些图像直接输入到detector中去进行检测。虽然这样的方法十分简单，但其效果仍然是最佳，也后续启发了SNIP这一系列的工作。单论性能而言，multiscale training/testing仍然是一个不可缺少的组件。然而其缺点也是很明显的，测试时间大幅度提高，对于实际使用并不友好。 另外一大类方法，也是Deep方法所独有的，也就是feature pyramid。最具代表性的工作便是经典的FPN了。这一类方法的思想是直接在feature层面上来近似image pyramid...

在深度学习目标检测中，特别是人脸检测中，由于分辨率低、图像模糊、信息少、噪声多，小目标和小人脸的检测一直是一个实用和常见的难点问题。然而，在过去几年的发展中，也出现了一些提高小目标检测性能的解决方案。本文将对这些方法进行分析、整理和总结。 图像金字塔和多尺度滑动窗口检测 一开始，在深学习方法成为流行之前，对于不同尺度的目标，通常是从原始图像开始，使用不同的分辨率构建图像金字塔，然后使用分类器对金字塔的每一层进行滑动窗口的目标检测。 在著名的人脸检测器MTCNN中，使用图像金字塔法检测不同分辨率的人脸目标。然而，这种方法通常是缓慢的，虽然构建图像金字塔可以使用卷积核分离加速或简单粗暴地缩放，但仍需要做多个特征提取，后来有人借其想法想出一个特征金字塔网络FPN，在不同层融合特征，只需要一次正向计...

简介 "Anchorfree"（无锚点）是一种目标检测方法，与传统的使用锚框（anchor boxes）的方法（例如Faster RCNN）不同。在传统方法中，锚框是预先定义的、具有不同尺寸和长宽比的矩形区域，用于捕捉不同尺寸和形状的目标。而在"anchorfree"方法中，不再使用锚框，而是直接预测目标的位置和形状，通常使用网络输出的热图和偏移信息。 以下是对"anchorfree"方法的一些关键理解点： 无需预定义锚框： 在传统目标检测方法中，需要事先定义和生成一组锚框，这可能需要大量的人工工作。而在"anchorfree"方法中，不再需要锚框，模型可以自动学习目标的位置和形状。 直接位置和形状回归： "anchorfree"方法通过输出的热图来表示目标的存在概率，并使用偏移信息来定位目...

YOLO的核心思想就是利用整张图作为网络的输入，直接在输出层回归bounding box的位置和bounding box所属的类别。 faster RCNN中也直接用整张图作为输入，但是fasterRCNN整体还是采用了RCNN那种 proposal+classifier的思想，只不过是将提取proposal的步骤放在CNN中实现了,而YOLO则采用直接回归的思路。 YOLO v1 将一幅图像分成SxS个网格(grid cell)，如果某个object的中心 落在这个网格中，则这个网格就负责预测这个object。 每个网格要预测B个bounding box，每个bounding box除了要回归自身的位置之外，还要附带预测一个confidence值。 这个confidence代表了所预测的b...

如何计算RF 公式一：这个算法从top往下层层迭代直到追溯回input image，从而计算出RF。 [公式] 其中，RF是感受野。RF和RF有点像，N代表 neighbour，指的是第n层的 a feature在n1层的RF，记住N_RF只是一个中间变量，不要和RF混淆。 stride是步长，ksize是卷积核大小。

背景 本文主要是《NICE: Nonlinear Independent Components Estimation》一文的介绍和实现。这篇文章也是glow这个模型的基础文章之一，可以说它就是glow的奠基石。 艰难的分布 众所周知，目前主流的生成模型包括VAE和GAN，但事实上除了这两个之外，还有基于flow的模型（flow可以直接翻译为“流”，它的概念我们后面再介绍）。事实上flow的历史和VAE、GAN它们一样悠久，但是flow却鲜为人知。在我看来，大概原因是flow找不到像GAN一样的诸如“造假者鉴别者”的直观解释吧，因为flow整体偏数学化，加上早期效果没有特别好但计算量又特别大，所以很难让人提起兴趣来。不过现在看来，OpenAI的这个好得让人惊叹的、基于flow的glow模型，估...

💡 原本随机采样的DDPM模型中，也隐含了一个确定性的采样过程DDIM，它的连续极限也是一个ODE。 细想上述过程，可以发现不管是“DDPM→DDIM”还是“SDE→ODE”，都是从随机采样模型过渡到确定性模型，而如果我们一开始的目标就是ODE，那么该过程未免显得有点“迂回”了。在本文中，笔者尝试给出ODE扩散模型的直接推导，并揭示了它与雅可比行列式、热传导方程等内容的联系。 Rectified Flow 理论推导 微分方程 像GAN这样的生成模型，它本质上是希望找到一个确定性变换，能将从简单分布（如标准正态分布）采样出来的随机变量，变换为特定数据分布的样本。flow模型也是生成模型之一，它的思路是反过来，先找到一个能将数据分布变换简单分布的可逆变换，再求解相应的逆变换来得到一个生成模型。 ...

DDPM 有一个非常明显的问题：采样过程很慢。因为 DDPM 的反向过程利用了马尔可夫假设，所以每次都必须在相邻的时间步之间进行去噪，而不能跳过中间步骤。原始论文使用了 1000 个时间步，所以我们在采样时也需要循环 1000 次去噪过程，这个过程是非常慢的。 为了加速 DDPM 的采样过程，DDIM 在不利用马尔可夫假设的情况下推导出了 diffusion 的反向过程，最终可以实现仅采样 20～100 步的情况下达到和 DDPM 采样 1000 步相近的生成效果，也就是提速 10～50 倍。这篇文章将对 DDIM 的理论进行讲解，并实现 DDIM 采样的代码。 DDPM 的反向过程 首先我们回顾一下 DDPM 反向过程的推导，为了推导出 [Math] 这个条件概率分布，DDPM 利用贝叶斯...

Diffusion Models from SDE 连续扩散模型 (Continuous Diffusion Models) 将传统的离散时间扩散过程扩展到连续时间域,可以被视为一个随机过程，使用随机微分方程(SDE)来描述。其前向过程可以写成如下形式： [公式] 其中， f(x,t) 可以看成偏移系数， g(t) 可以看成是扩散系数， dw 是标准布朗运动。这个SDE 描述了数据在连续时间域内如何被噪声逐渐破坏。 这个随机过程的逆向过程存在（更准确的描述：下面的逆向时间SDE具有与正向过程SDE相同的联合分布）为 [公式] 前面我们得到了扩散过程的逆向过程可以用一个SDE描述(逆向随机过程),事实上，存在一个确定性过程 (用ODE描述)也是它的逆向过程 (更准确的描述：这个ODE过程的在任...