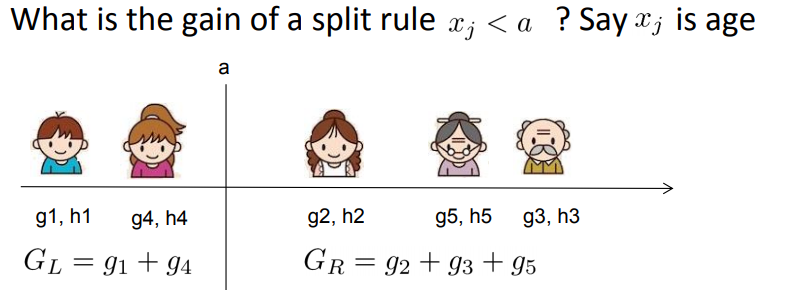INCOMING TRANSMISSION

76. 最小覆盖子串 题目 给定两个字符串 s 和 t ，长度分别是 m 和 n ，返回 s 中的 最短窗口 子串 ，使得该子串包含 t 中的每一个字符（ 包括重复字符 ）。如果没有这样的子串，返回空字符串 "" 。 测试用例保证答案唯一。 示例 1： 输入：s = "ADOBECODEBANC", t = "ABC" 输出："BANC" 解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。 示例 2： 输入：s = "a", t = "a" 输出："a" 解释：整个字符串 s 是最小覆盖子串。 示例 3: 输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中， 因此没有符合条件的子字符串，返回空字符串。 提示： m == s.length n == t.length 1 <= m, n <= 10 5 s 和 t 由英文字母组成 题解 这是一个经典的 滑动窗口 (Sliding Window) 问题 我们需要维护一个动态的窗口 [left, right] ： 右移扩大 ：不断移动...

简介 如果以概率的视角看待世界的生成模型。 在这样的世界观中，我们可以将任何类型的观察数据（例如 \(D\) ）视为来自底层分布（例如 \( p_{data}\) ）的有限样本集。 任何生成模型的目标都是在访问数据集 \(D\) 的情况下近似该数据分布。 如果我们能够学习到一个好的生成模型，我们可以将学习到的模型用于下游推理。 我们主要对数据分布的参数近似感兴趣，在一组有限的参数中，它总结了关于数据集 \(D\) 的所有信息。 与非参数模型相比，参数模型在处理大型数据集时能够更有效地扩展，但受限于可以表示的分布族。 在参数的设置中，我们可以将学习生成模型的任务视为在模型分布族中挑选参数，以最小化模型分布和数据分布之间的距离。 如上图，给定一个狗的图像数据集，我们的目标是学习模型族 \(M\) 中生成模型 θ 的参数，使得模型分布 \(p_θ\) 接近 \(p_{data}\) 上的数据分布。 在数学上，我们可以将我们的目标指定为以下优化问题: \[\mathop{min}\limits_{\theta\in M}d(p_\theta,p_{data})\] 其中， \(d()\)...

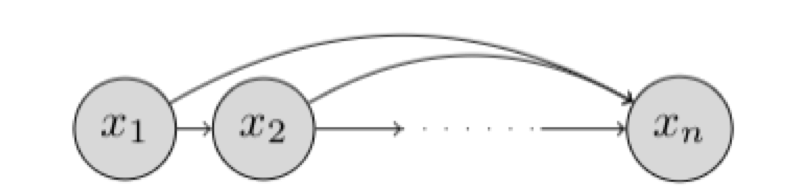
研究对象与基本设定 我们希望学习一个能够“生成数据”的概率模型。假设我们有一个数据集 \(D\) ，每个样本是 \(n\) 维二值向量： \(x \in \{0,1\}^n\) 我们的目标是用一个参数化分布 \(p_\theta(x)\) 去逼近真实数据分布 \(p_{\text{data}}(x)\) ，并最终能够： 密度估计 ：给定 \(x\) 计算 \(p_\theta(x)\) 或 \(\log p_\theta(x)\) 采样生成 ：从 \(p_\theta(x)\) 采样得到新的 \(x\) 表示：链式法则与自回归分解 链式法则分解联合分布 任意联合分布都可用概率链式法则分解为条件概率的乘积： \[p(x) = \prod_{i=1}^{n} p(x_i \mid x_1, x_2, \dots, x_{i-1}) = \prod_{i=1}^{n} p(x_i \mid x_{<i})\] 其中： \(x_{<i} = [x_1, x_2, \dots, x_{i-1}]\) ，这意味着：只要我们能为每个维度 \(i\) 学好一个条件分布 \(p(x_i \mid...

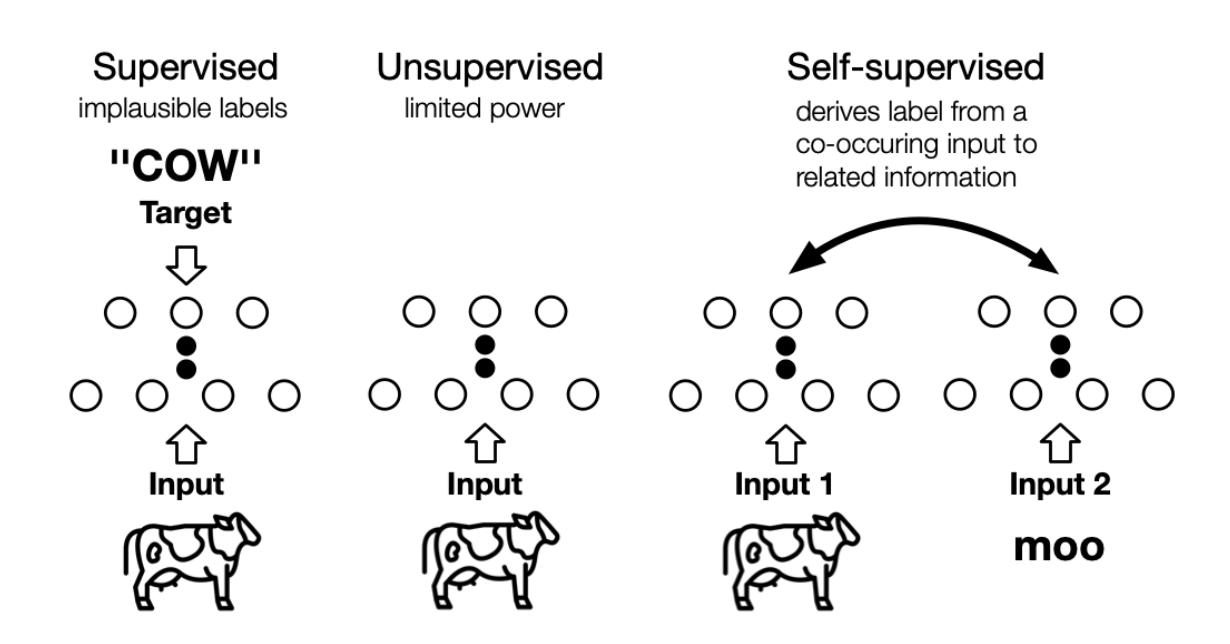
the machine predicts any parts of its input for any observed part 这是LeCun在AAAI 2020上对自监督学习的定义，再结合传统的自监督学习定义，可以总结如下两点特征： 通过“半自动”过程从数据本身获取“标签”； 从“其他部分”预测部分数据。 个人理解， 其实任意挖掘对象之间联系、探索不同对象共同本质的方法，都或多或少算是自监督学习的思想 。 自监督学习与无监督学习的区别主要在于，无监督学习专注于检测特定的数据模式，如聚类、社区发现或异常检测，而自监督学习的目标是恢复（recovering），仍处于监督学习的范式中。上图展示了三者之间的区别， 自监督中的“related information” 可以来自其他模态、输入的其他部分以及输入的不同形式。 Self-Supervised...

随机森林 (Random Forests) 是一种利用CART决策树作为基学习器的 Bagging 集成学习算法。随机森林模型的构建过程如下： 数据采样 作为一种 Bagging 集成算法，随机森林同样采用有放回的采样，对于总体训练集 T ，抽样一个子集 T_{sub} 作为训练样本集。除此之外，假设训练集的特征个数为 d ，每次仅选择 k(k<d) 个构建决策树。因此，随机森林除了能够做到样本扰动外，还添加了特征扰动，对于特征的选择个数，推荐值为 k=log_2⁡d 。 树的构建 每次根据采样得到的数据和特征构建一棵决策树。在构建决策树的过程中，会让决策树生长完全而不进行剪枝。构建出的若干棵决策树则组成了最终的随机森林。 随机森林在众多分类算法中表现十分出众，其主要的优点包括： 1. 由于...

AdaBoost基本思路 分类问题 Adaboost 是 Boosting 算法中有代表性的一个。原始的 Adaboost 算法用于解决二分类问题，因此对于一个训练集 [公式] 其中 [Math] ，，首先初始化训练集的权重 [公式] 根据每一轮训练集的权重 D_m ，对训练集数据进行抽样得到 T_m ，再根据 T_m 训练得到每一轮的基学习器 h_m 。通过计算可以得出基学习器 h_m 的误差为 e_m [公式] 根据基学习器的误差计算得出该基学习器在最终学习器中的权重系数 [公式] 为什么这样计算弱学习器权重系数？从上式可以看出，如果分类误差率 𝑒_𝑘 越大，则对应的弱分类器权重系数 [Math] 越小。也就是说，误差率小的弱分类器权重系数越大。具体为什么采用这个权重系数公式，见AdaB...

GBDT (Gradient Boosting Decision Tree) 是另一种基于 Boosting 思想的集成算法，除此之外 GBDT 还有很多其他的叫法，例如：GBM (Gradient Boosting Machine)，GBRT (Gradient Boosting Regression Tree)，MART (Multiple Additive Regression Tree) 等等。GBDT 算法由 3 个主要概念构成：Gradient Boosting (GB)，Regression Decision Tree (DT 或 RT) 和 Shrinkage。 0. Decision Tree：CART回归树 首先，GBDT使用的决策树是CART回归树，无论是处理回归问题还...

1. 从GBDT到XGBoost 作为GBDT的高效实现，XGBoost是一个上限特别高的算法，因此在算法竞赛中比较受欢迎。简单来说，对比原算法GBDT，XGBoost主要从下面三个方面做了优化： 一是算法本身的优化：在算法的弱学习器模型选择上，对比GBDT只支持决策树，还可以选择很多其他的弱学习器。在算法的损失函数上，除了本身的损失，还加上了正则化部分。在算法的优化方式上，GBDT的损失函数只对误差部分做负梯度（一阶泰勒）展开，而XGBoost损失函数对误差部分做二阶泰勒展开，更加准确。算法本身的优化是我们后面讨论的重点。 二是算法运行效率的优化：对每个弱学习器，比如决策树建立的过程做并行选择，找到合适的子树分裂特征和特征值。在并行选择之前，先对所有的特征的值进行排序分组，方便前面说的并行...

问题表示 有很多概率问题，尤其是独立重复实验问题，如果用生成函数的方法来做，会显得特别方便。本文要讲的“随机游走”问题便是其中一例，它又被形象地叫做“醉汉问题”，其本质上是一个二项分布，但是由于取了极限，出现了很多新的性质和应用。我们先考虑如下问题： 考虑实数轴上的一个粒子，在 t=0 时刻它位于原点，每过一秒，它要不向前移动一格（+1），要不就向后移动一格（1），问 n 秒后它所处位置的概率分布。 不难发现，这个问题跟二项分布是雷同的。如果把这个粒子形象比喻成一个“喝醉酒的人”，那么上面的走法就类似于一个完全不省人事的醉汉走路问题了。（当然，醉汉是在三维空间走路的，这里简单起见，只描述了一维...

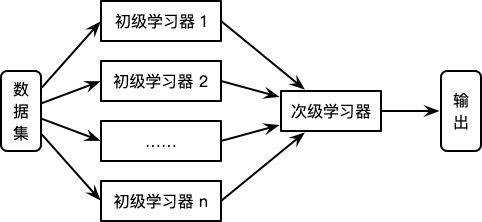
这篇博客介绍一下集成学习的几类：Bagging，Boosting以及Stacking。 传统机器学习算法 (例如：决策树，人工神经网络，支持向量机，朴素贝叶斯等) 的目标都是寻找一个最优分类器尽可能的将训练数据分开。集成学习 (Ensemble Learning) 算法的基本思想就是将多个分类器组合，从而实现一个预测效果更好的集成分类器。集成算法可以说从一方面验证了中国的一句老话：三个臭皮匠，赛过诸葛亮。 Thomas G. Dietterich 指出了集成算法在统计，计算和表示上的有效原因： 统计上的原因 一个学习算法可以理解为在一个假设空间 H 中选找到一个最好的假设。但是，当训练样本的数据量小到不够用来精确的学习到目标假设时，学习算法可以找到很多满足训练样本的分类器。所以，学习算法选择...

给定一个包含 n 维数据 x 的数据集 D , 简单起见，假设数据 [Math] . 由于真正对联合分布建模的时候， x，y 都是随机变量，故而只需讨论 p(X)=p(x_1,...,x_n) 即可，毕竟只需要令 x_n=y 即可。 给定一个具体的任务，如MNIST中的手写数字二值图分类，从Generative的角度进行Represent，并在Inference中Learning. 下面先介绍： 描述如何对这个MINST任务建模 p(X,Y) （Representation） 对MNIST任务建模 对于一张pixel为 [Math] 大小的图片，令 x_1 表示第一个pixel的随机变量， [Math] ，需明确： 任务目标：学习一个模型分布 [Math] ，使采样时 [Math] ， x ...

问题定义 多元二次多项式，维度为 n ，那么可以用以下公式描述该函数： [Formula] 其中 a_{i,j} 为二次项系数，共有 n^2 项， 1≤i,j≤n ，且所有的 a 不全为0，即 ∃a_{i,j}≠0 ; b_k 为一次项系数，共 n 项， 1≤k≤n ; c 为常数项。 记 f(x)=[x_1,x_2,...,x_n]^T ，则上述函数可以写作二次型的形式： 转化过程中A,b满足： A 为n阶对称方阵， A_{i,j}=a_{i,j} 因为 ∃a_{i,j}≠0 ，A不为零矩阵 b_i=b_i 为了后续计算简便，我们将二次型稍作改动： [Formula] 我们的目标就是寻找该函...