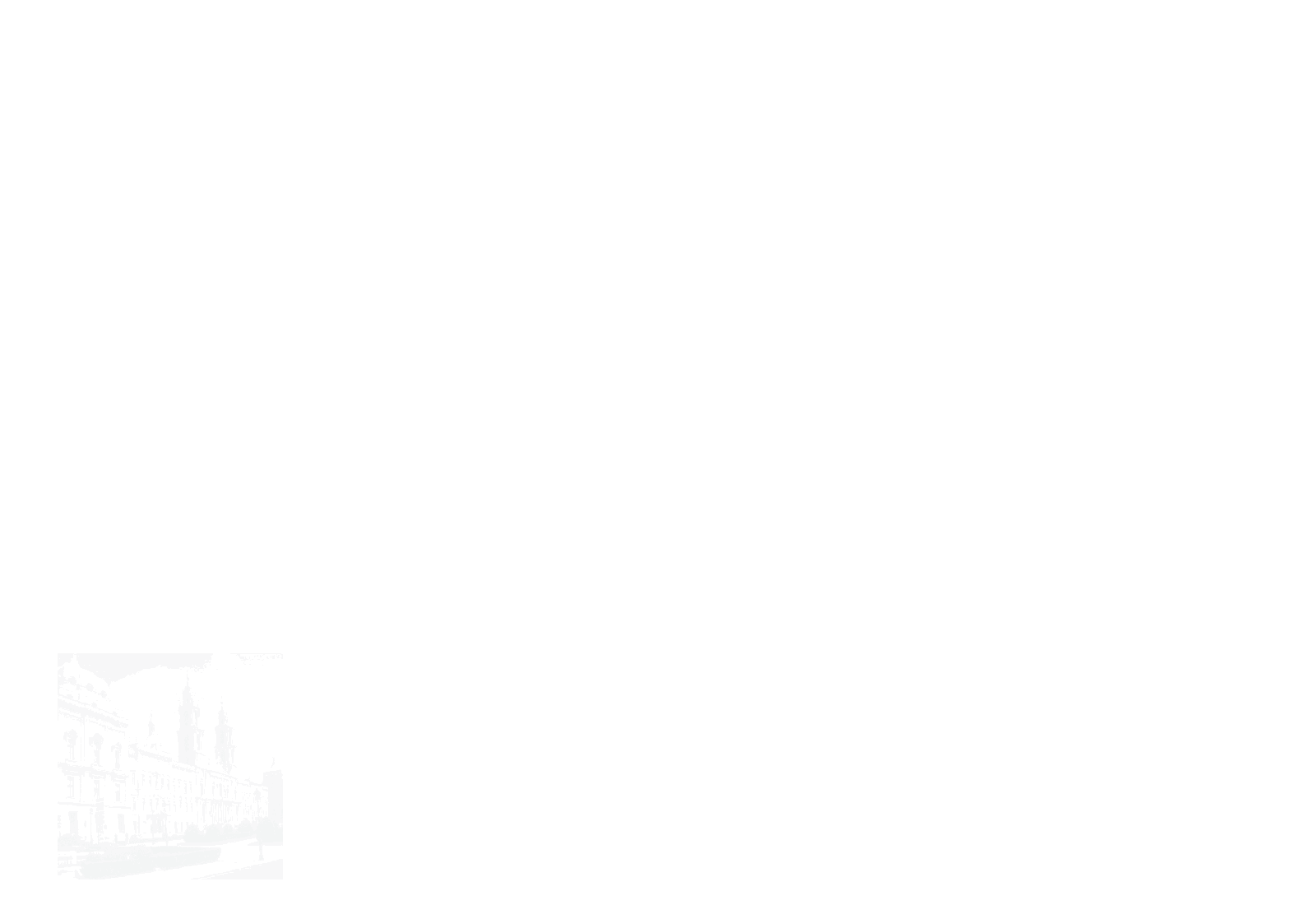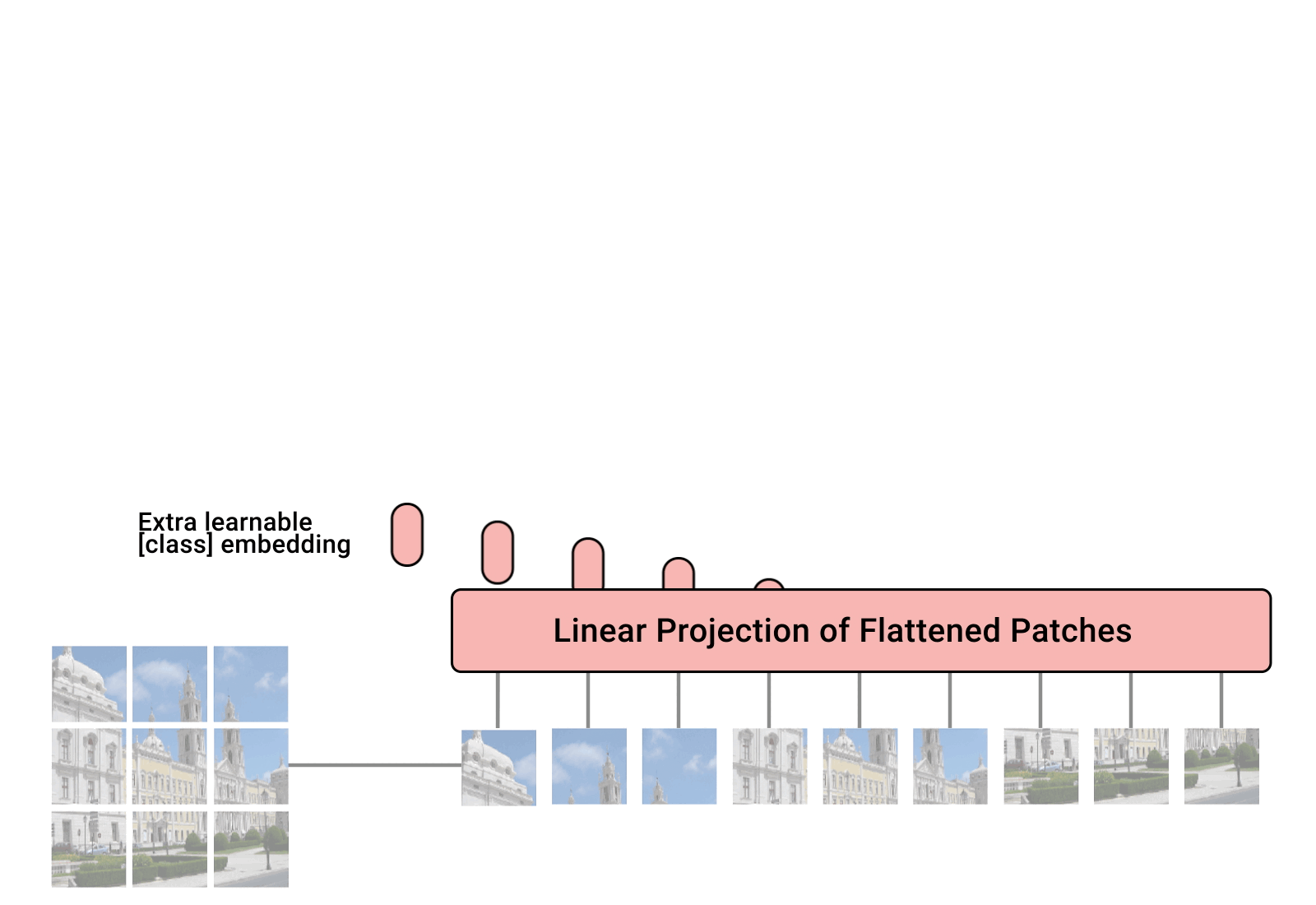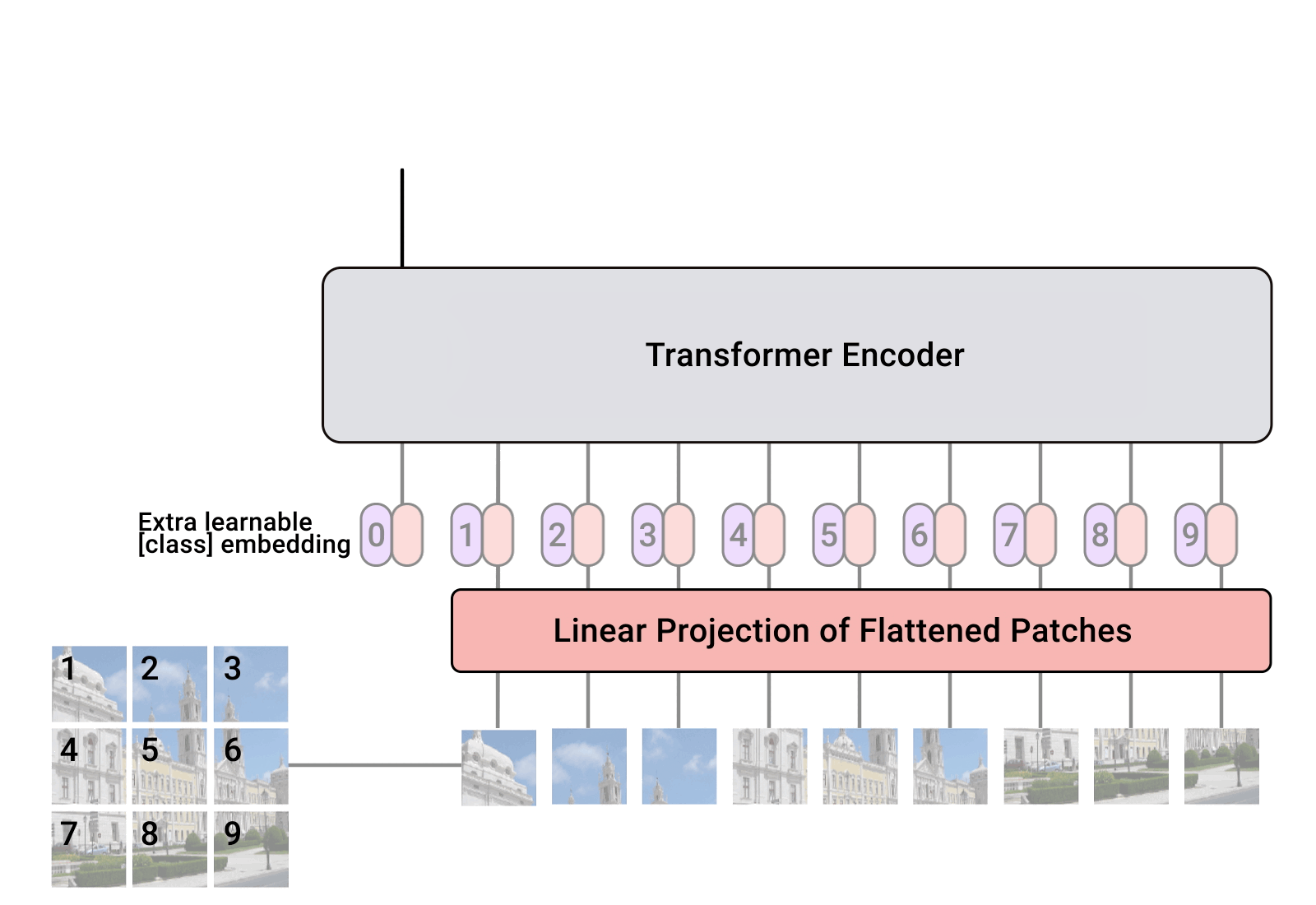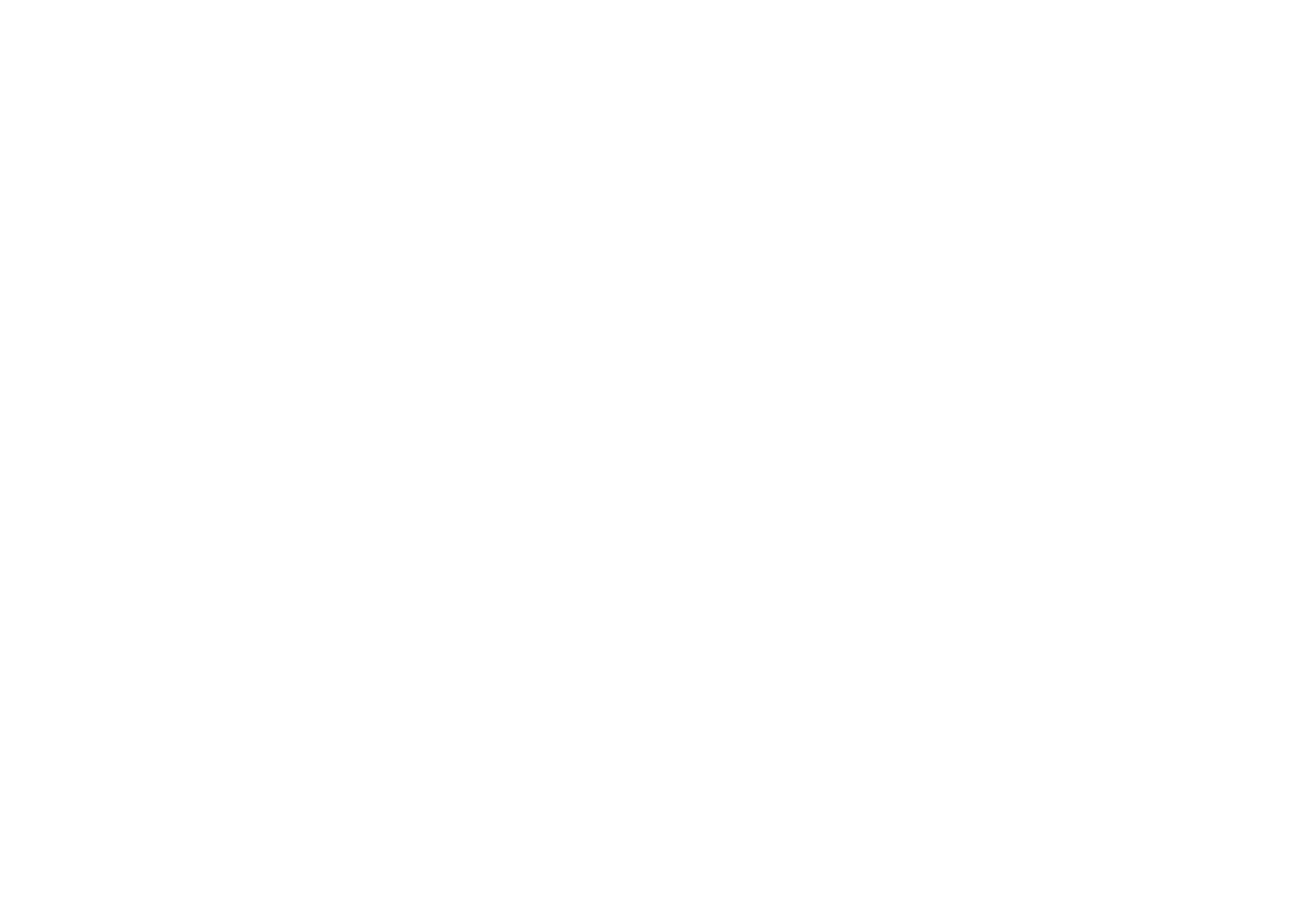INCOMING TRANSMISSION

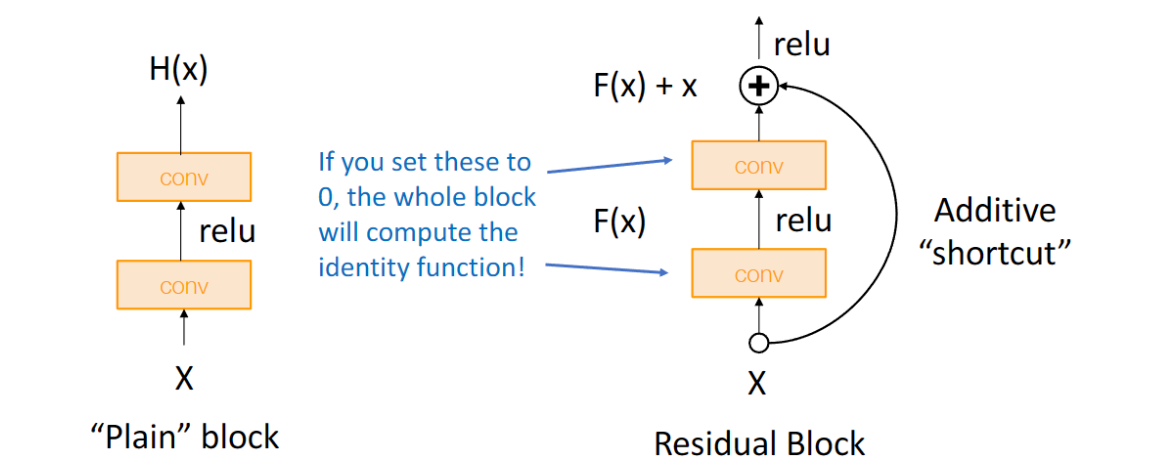
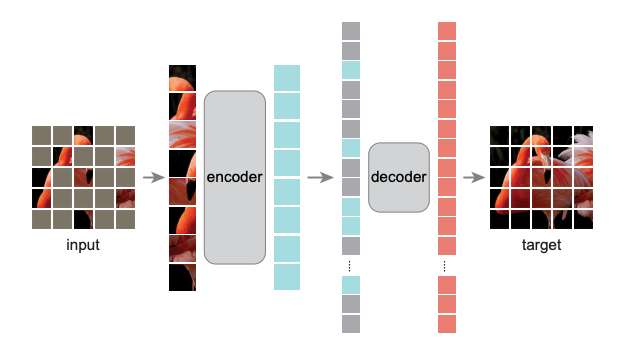
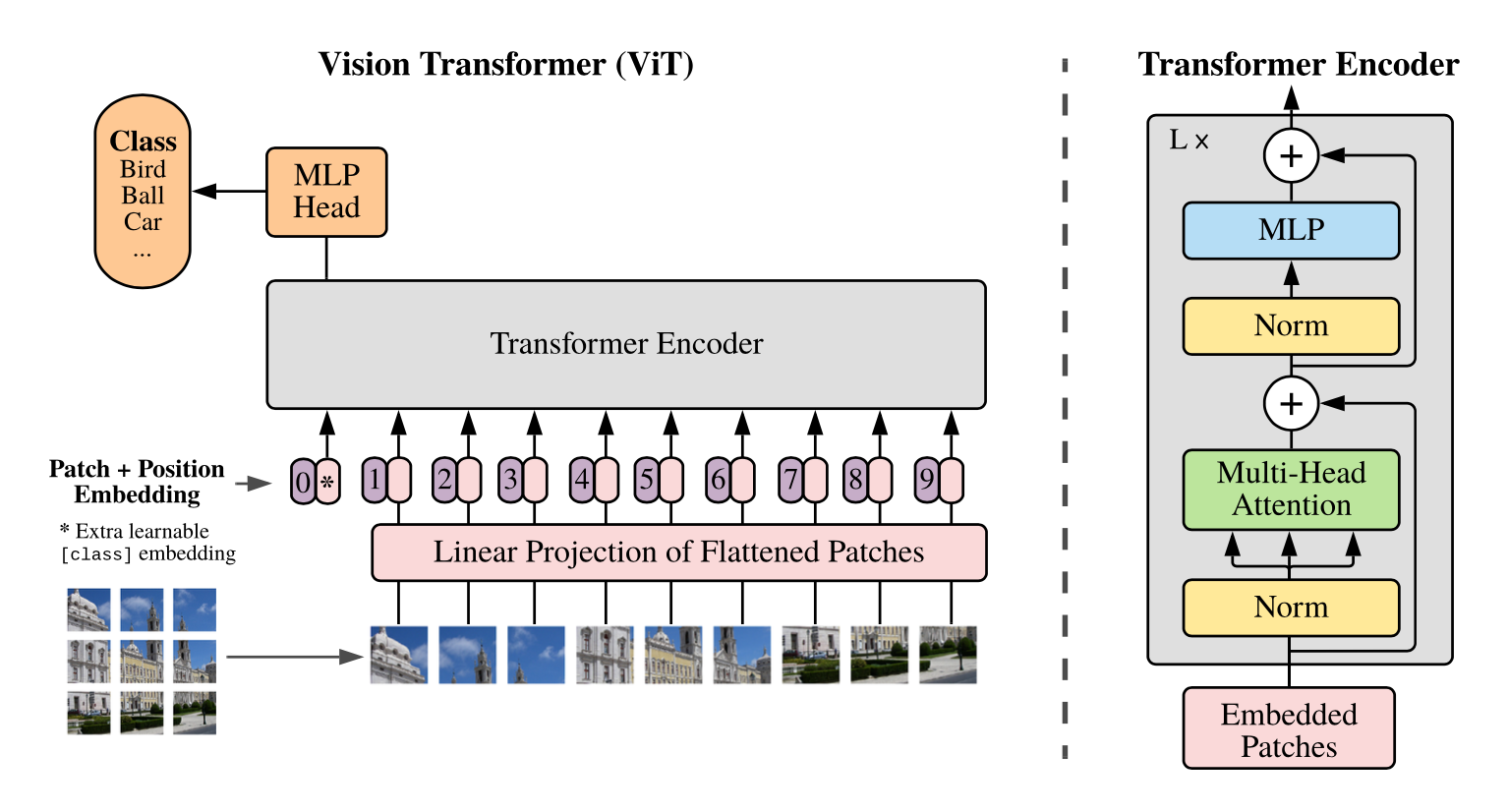
总览 由于是“图文多模态”，还是要从“图”和“文”的表征方法讲起，然后讲清楚图文表征的融合方法。这里只讲两件事情： 视觉表征 ：分为两个部分问题，一是如何合理建模视觉输入特征，二是如何通过预训练手段进行充分学习表征，这两点是基于视觉完成具体算法任务的基础； 视觉与自然语言的对齐（Visul Language Alignment）或融合 ：目的是将视觉和自然语言建模到同一表征空间并进行融合，实现自然语言和视觉语义的互通，这点同样离不开预训练这一过程。模态对齐是处理多模态问题的基础，也是现在流行的多模态大模型技术前提。 对于视觉表征，从发展上可以分为卷积神经网络（CNN）和Vision Transformer（VIT）两大脉络，二者分别都有各自的表征、预训练以及多模态对齐的发展过程。而对于VIT线，另有多模态大模型如火如荼的发展，可谓日新月异。 CNN：视觉理解的一代先驱 点击展开 卷积视觉表征模型和预训练...

文章从连续情形出发开始介绍重参数，主要的例子是正态分布的重参数；然后引入离散分布的重参数，这就涉及到了Gumbel Softmax，包括Gumbel Softmax的一些证明和讨论；最后再讲讲重参数背后的一些故事，这主要跟梯度估计有关。 基本概念 重参数（Reparameterization） 实际上是处理如下期望形式的目标函数的一种技巧： \[L_{\theta}=\mathbb{E}_{z\sim p_{\theta}(z)}[f(z)]\tag{1}\] 这样的目标在VAE中会出现，在文本GAN也会出现，在强化学习中也会出现（ \(f(z)\) 对应于奖励函数），所以深究下去，我们会经常碰到这样的目标函数。取决于 \(z\) 的连续性，它对应不同的形式： \[\int p_{\theta}(z) f(z)dz\,\,\,\text{(连续情形)}\qquad\qquad \sum_{z} p_{\theta}(z) f(z)\,\,\,\text{(离散情形)}\tag{2}\] 当然，离散情况下我们更喜欢将记号 \(z\) 换成 \(y\) 或者 \(c\) 。 为了最小化...

导言 自监督学习（Self-Supervised Learning）能利用大量无标注的数据进行表征学习，然后在特定下游任务上对参数进行微调。通过这样的方式，能够在较少有标注数据上取得优于有监督学习方法的精度。近年来，自监督学习受到了越来越多的关注，如Yann Lecun也在 AAAI 上讲 Self-Supervised Learning 是未来的大势所趋。在CV领域涌现了如SwAV、MOCO、DINO、MoBY等一系列工作。MAE是kaiming继MOCO之后在自监督学习领域的又一力作。首先，本文会对MAE进行解读，然后基于EasyCV库的精度复现过程及其中遇到的一些问题作出解答。 概述 MAE的做法很简单：随机mask掉图片中的一些patch，然后通过模型去重建这些丢失的区域。包括两个核心的设计：1.非对称编码-解码结构 2.用较高的掩码率（75%）。通过这两个设计MAE在预训练过程中可以取得3倍以上的训练速度和更高的精度，如ViT-Huge能够通过ImageNet-1K数据上取得87.8%的准确率。 模型拆解...

概述 在计算机视觉领域（CV），对视觉特征的理解CNN是长期处于主导地位的。而在NLP领域，Transformer框架的巨大成功，也激发了不少研究者探索将Transformer用于计算机视觉任务。ViT（Vision Transformer）的出现标志着在CV领域Transformer架构迈出了重要的一步。尤其在当前结合LLM的多模态探索上（MM-LLM），都是以LLM大语言模型为骨干架构的模型，多种模态的信息需要先做token化处理，再输入到LLM模型。ViT天然具有序列化特征的建模能力，自然在MM-LLM探索中大放异彩~ ViT在多模态模型中的角色类似于自然语言建模中的Tokenizer组件，对图像进行视觉特征编码，产出图像的序列特征。只不过ViT的编码过程本身也是采用了Transformer的模型结构。 本文主要结合几篇paper和源码讲讲ViT和针对ViT的一些优化方法~ ViT（Vision Transformer）...

ViT（vision transformer）是Google在2020年提出的直接将transformer应用在图像分类的模型，后面很多的工作都是基于ViT进行改进的。ViT的思路很简单：直接把图像分成固定大小的patchs，然后通过线性变换得到patch embedding，这就类比NLP的words和word embedding，由于transformer的输入就是a sequence of token embeddings，所以将图像的patch embeddings送入transformer后就能够进行特征提取从而分类了。ViT模型原理如下图所示，其实ViT模型只是用了transformer的Encoder来提取特征（原始的transformer还有decoder部分，用于实现sequence to sequence，比如机器翻译）。下面将分别对各个部分做详细的介绍。 Patch Embedding 对于ViT来说，首先要将原始的2-D图像转换成一系列1-D的patch embeddings，这就好似NLP中的word embedding。输入的2-D图像记为 \(x\in...

这是一篇尝试改变LLM「范式」的文章：当前主流的LLM架构都是「自回归」的，通俗地理解就是必须「从左到右依次生成」。这篇文章挑战了这一范式，探索扩散模型在 LLMs 上的可行性，通过 随机掩码 - 预测 的逆向思维，让模型学会「全局思考」。 论文： [2502.09992] Large Language Diffusion Models 背景 主流大语言模型架构：自回归模型 (Autoregressive LLMs) 过去几年， 自回归模型（Autoregressive Models, ARMs）一直是大语言模型(LLM)的主流架构​。典型的自回归语言模型以Transformer解码器为基础，按照从左到右 的顺序依次预测下一个词元(token)。 形式化地，自回归模型将一个长度为 \(N\) 的文本序列 \(X=(x_1, x_2, ..., x_N)\) 的概率分解为各位置的条件概率连乘积​： \[P_{\theta}(x_1, x_2, \dots, x_N) = \prod_{i=1}^{N} P_{\theta}(x_i \mid x_1, x_2, \dots,...

引言 Diffusion模型近年来在图像生成这一连续域任务中取得了显著成果，展现出强大的生成能力。然而，在文本生成这一离散域任务中整体效果仍不尽如人意，未能在该领域引起广泛关注。 去年，一篇研究离散扩散模型在文本生成的文章《Discrete Diffusion Modeling by Estimating the Ratios of the Data Distribution》获得ICML 2024的Best Paper，引发了学术界的广泛兴趣，也激发了新一轮的研究热潮。随后在2025年，越来越多高校和企业也开始积极探索基于Diffusion的文本生成方法。其中，近期备受关注的Block Diffusion也成功入选ICLR oral，进一步推动了该方向的发展。...

💡 扩散模型：通过加噪的方式去学习原始数据的分布， 从学到的分布中去生成样本 DDPM 关键点： 1. 正向加噪是离散时间马尔可夫链：从 \(x_0\) 逐步加噪得到 \(x_1,x_2,...,x_T\) ；在合适的噪声调度与足够大的 \(T\) 下， \(x_T\) 近似服从 \( N(0,I) \) 的各向同性高斯。 2. 每一步噪声方差 \(β_t\) 满足 \(0<β_t<1\) ，通常随 \(t\) 增大；因此 \(q(x_t|x_{t-1}) \) 的均值缩放系数 \(\sqrt{1-β_t} \) 逐渐减小。 3. 训练通过最大化对数似然的变分下界（ELBO）来学习反向过程 \( p_θ(x_{t-1}|x_t)\) ，并将其参数化为高斯分布（神经网络预测均值/噪声或 score）。 4. 将目标写成 score/DSM 形式时，loss 的权重与对应噪声层的方差尺度（如 \(1-\bar{α}_t\) 或相关量）有关；采样通常是按学习到的反向转移逐步生成（祖先采样），与经典 Langevin MCMC 更新形式不同，但可在 SDE 视角下统一理解。...

基于文章 《Elucidating the Design Space of Diffusion-Based Generative Models》 来统一扩散模型框架 通用扩散模型框架推导 加噪公式 Flow Matching的一步加噪公式 \[\mathbf{x}_t=(1-t)\mathbf{x}_0+t\varepsilon\] 写成概率分布形式： \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;(1-t)\mathbf{x}_0,t^2\mathbf{I})\] Score Matching的一步加噪公式 \[\mathbf{x}_t=\mathbf{x}_0+\sigma_t\varepsilon \] 写成概率分布形式： \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;\mathbf{x}_0,\sigma_t^2\mathbf{I})\] DDPM/DDIM的一步加噪公式...

简介 如果以概率的视角看待世界的生成模型。 在这样的世界观中，我们可以将任何类型的观察数据（例如 \(D\) ）视为来自底层分布（例如 \( p_{data}\) ）的有限样本集。 任何生成模型的目标都是在访问数据集 \(D\) 的情况下近似该数据分布。 如果我们能够学习到一个好的生成模型，我们可以将学习到的模型用于下游推理。 我们主要对数据分布的参数近似感兴趣，在一组有限的参数中，它总结了关于数据集 \(D\) 的所有信息。 与非参数模型相比，参数模型在处理大型数据集时能够更有效地扩展，但受限于可以表示的分布族。 在参数的设置中，我们可以将学习生成模型的任务视为在模型分布族中挑选参数，以最小化模型分布和数据分布之间的距离。 如上图，给定一个狗的图像数据集，我们的目标是学习模型族 \(M\) 中生成模型 θ 的参数，使得模型分布 \(p_θ\) 接近 \(p_{data}\) 上的数据分布。 在数学上，我们可以将我们的目标指定为以下优化问题: \[\mathop{min}\limits_{\theta\in M}d(p_\theta,p_{data})\] 其中， \(d()\)...