INCOMING TRANSMISSION

128. 最长连续序列 题目 给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 1： 输入：nums = [100,4,200,1,3,2] 输出：4 解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。 示例 2： 输入：nums = [0,3,7,2,5,8,4,6,0,1] 输出：9 示例 3： 输入：nums = [1,0,1,2] 输出：3 提示： 0 <= nums.length <= 10 5 -10 9 <= nums[i] <= 10 9 题解 我们需要在 \(O(1)\) 的时间内查找某个数是否存在。因此，首先将数组中的所有元素放入一个 HashSet 中。这不仅能去重，还能支持快速查找。 避免冗余计算 (关键优化) 如果我们对集合中的每一个数都尝试去向后计数（例如，对于 x ，尝试找 x+1 , x+2 ...），最坏情况下的时间复杂度会退化到 \(O(n^2)\) 。 优化策略 ： 我们 只从序列的起点开始计数 。...

76. 最小覆盖子串 题目 给定两个字符串 s 和 t ，长度分别是 m 和 n ，返回 s 中的 最短窗口 子串 ，使得该子串包含 t 中的每一个字符（ 包括重复字符 ）。如果没有这样的子串，返回空字符串 "" 。 测试用例保证答案唯一。 示例 1： 输入：s = "ADOBECODEBANC", t = "ABC" 输出："BANC" 解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。 示例 2： 输入：s = "a", t = "a" 输出："a" 解释：整个字符串 s 是最小覆盖子串。 示例 3: 输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中， 因此没有符合条件的子字符串，返回空字符串。 提示： m == s.length n == t.length 1 <= m, n <= 10 5 s 和 t 由英文字母组成 题解 这是一个经典的 滑动窗口 (Sliding Window) 问题 我们需要维护一个动态的窗口 [left, right] ： 右移扩大 ：不断移动...

129. 滑动窗口最大值 题目 给你一个整数数组 nums ，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 示例 1： 输入：nums = [1,3,-1,-3,5,3,6,7], k = 3 输出：[3,3,5,5,6,7] 解释： 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7 示例 2： 输入：nums = [1], k = 1 输出：[1] 提示： 1 <= nums.length...

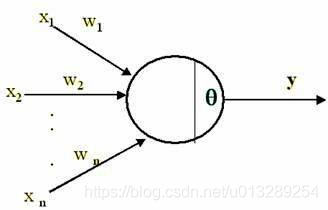
1.深度学习偏置的作用？ 我们在学深度学习的时候，最早接触到的神经网络应该属于感知器（感知器本身就是一个很简单的神经网络，也许有人认为它不属于神经网络，当然认为它和神经网络长得像也行） 要想激活这个感知器，使得 y=1 ，就必须使 x_1w_1 + x_2w_2 +....+x_nw_n T （ T 为一个阈值），而 T 越大，想激活这个感知器的难度越大，人工选择一个阈值并不是一个好的方法，因为样本那么多，我不可能手动选择一个阈值，使得模型整体表现最佳，那么我们可以使得T变成可学习的，这样一来， T 会自动学习到一个数，使得模型的整体表现最佳。当把T移动到左边，它就成了偏置， x_1w_1 + x_2w_2 +....+x_nw_n T 0 xw +b 0 ，总之，偏置的大小控制着激活这个感...

如何计算RF 公式一：这个算法从top往下层层迭代直到追溯回input image，从而计算出RF。 [公式] 其中，RF是感受野。RF和RF有点像，N代表 neighbour，指的是第n层的 a feature在n1层的RF，记住N_RF只是一个中间变量，不要和RF混淆。 stride是步长，ksize是卷积核大小。

引言与背景 蒙特卡洛方法是强化学习中的重要算法类别，它标志着从基于模型到无模型算法的转变。这类算法不依赖环境模型，而是通过与环境的直接交互获取经验数据来学习最优策略。 蒙特卡洛方法在强化学习算法谱系中处于"无模型"方法的起始位置，是从基于模型的方法（如值迭代和策略迭代）向无模型方法过渡的第一步。 无模型强化学习的核心理念可以简述为：如果没有模型，我们必须有数据；如果没有数据，我们必须有模型；如果两者都没有，我们就无法找到最优策略。在强化学习中，"数据"通常指智能体与环境交互的经验。 均值估计问题 在介绍蒙特卡洛强化学习算法之前，我们首先需要理解均值估计问题，这是理解从数据而非模型中学习的基础。 考虑一个可以取有限实数集合 X 中值的随机变量 X ，我们的任务是计算 X 的均值或期望值： E[...

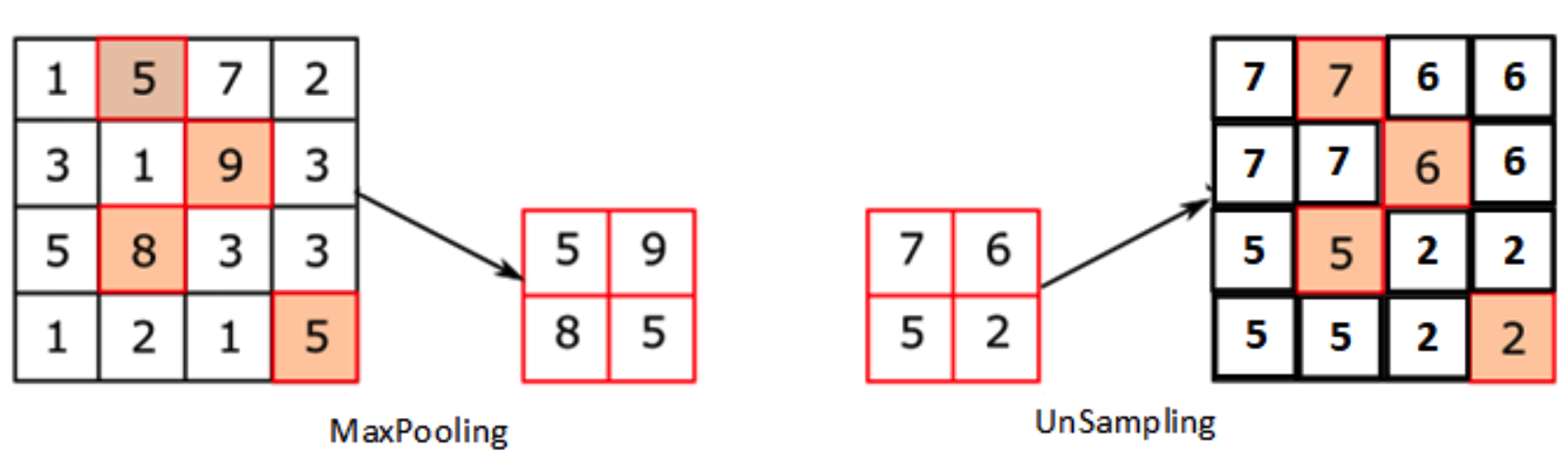
通过卷积和池化等技术可以将图像进行降维，因此，一些研究人员也想办法恢复原分辨率大小的图像，特别是在语义分割领域应用很成熟。 1、Upsampling（上采样）[没有学习过程] 在FCN、Unet等网络结构中，涉及到了上采样。上采样概念：上采样指的是任何可以让图像变成更高分辨率的技术。最简单的方式是重采样和插值：将输入图片进行rescale到一个想要的尺寸，而且计算每个点的像素点，使用如双线性插值等插值方法对其余点进行插值来完成上采样过程。 在PyTorch中，上采样的层被封装在torch.nn中的Vision Layers里面，一共有4种： PixelShuffle Upsample UpsamplingNearest2d UpsamplingBilinear2d 0）PixelShuffl...

引言与背景 价值函数方法是强化学习中的核心技术，它解决了传统表格方法在处理大型状态或动作空间时的效率问题。本文探讨了从表格表示向函数表示的转变，这是强化学习算法发展的重要里程碑。 在强化学习的发展路径中，价值函数方法位于从基于模型到无模型、从表格表示到函数表示的演进过程中。它结合了时序差分学习的思想，并通过函数近似技术来处理复杂环境。 价值表示：从表格到函数 表格与函数表示的对比 传统的表格方法将状态值存储在一个表格中： 而函数近似方法则使用参数化函数来表示这些值，例如： [公式] 其中 [Math] 称作是状态 s 的特征向量， w 是参数向量。 两种不同的表现形式的区别主要体现在以下几个方面： 值的检索方式 值的更新方式 函数复杂度与近似能力 函数的复杂度决定了其近似的能力： 一阶线性函...

引言 时序差分（TemporalDifference，TD）方法是强化学习中的一类核心算法，它结合了动态规划与蒙特卡洛方法的优点。TD方法是无模型（modelfree）学习方法，不需要环境模型即可学习价值函数和最优策略。 TD方法的核心特点是通过比较不同时间步骤的估计值之间的差异来更新价值函数，这种差异被称为"时序差分误差"（TD error）。TD方法可以被视为解决贝尔曼方程或贝尔曼最优方程的特殊随机逼近算法。 基础TD算法：状态值函数学习 给定策略 [Math] ，基础TD算法用于估计状态值函数 [Math] 。假设我们有一些按照策略 [Math] 生成的经验样本 (s_0, r_1, s_1, ..., s_t, r_{t+1}, s_{t+1}, ...) ，TD算法的更新规则为： ...