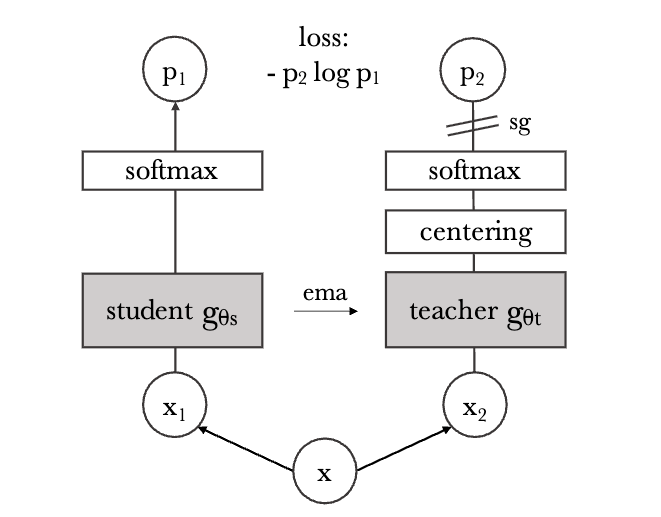
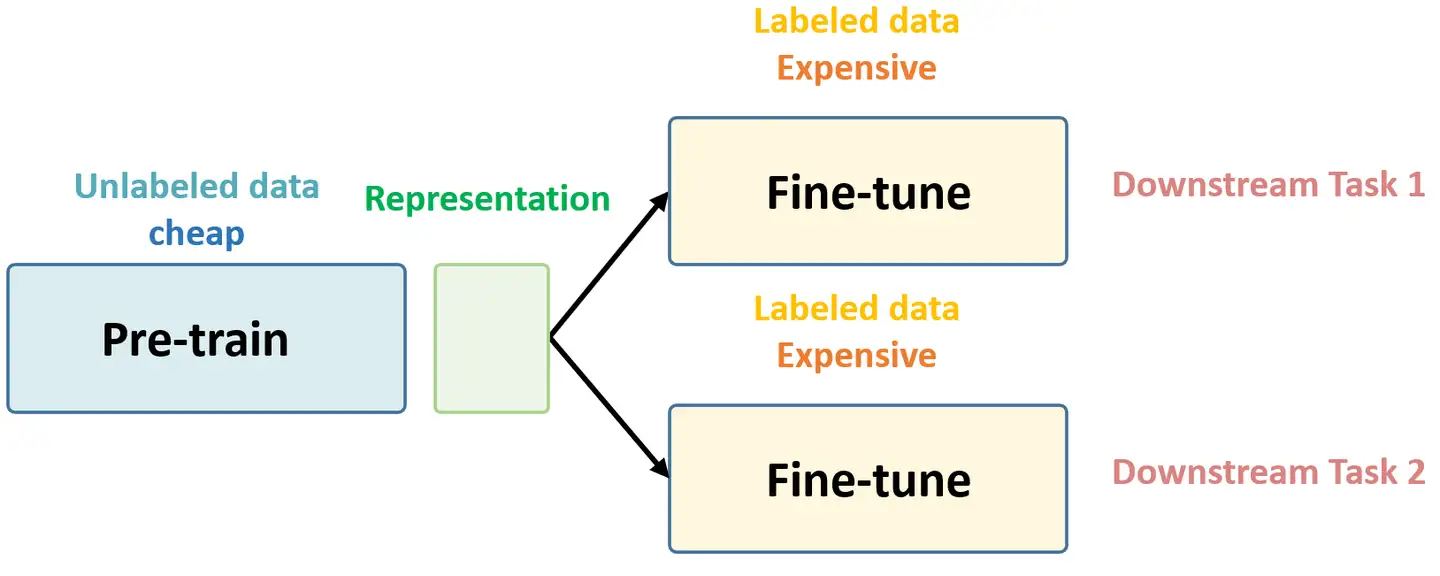
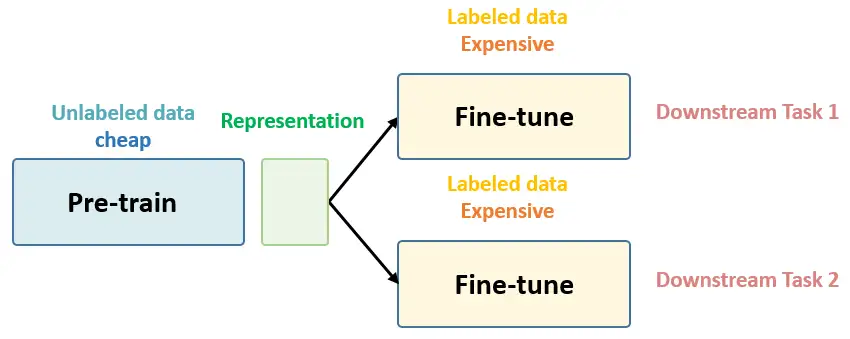
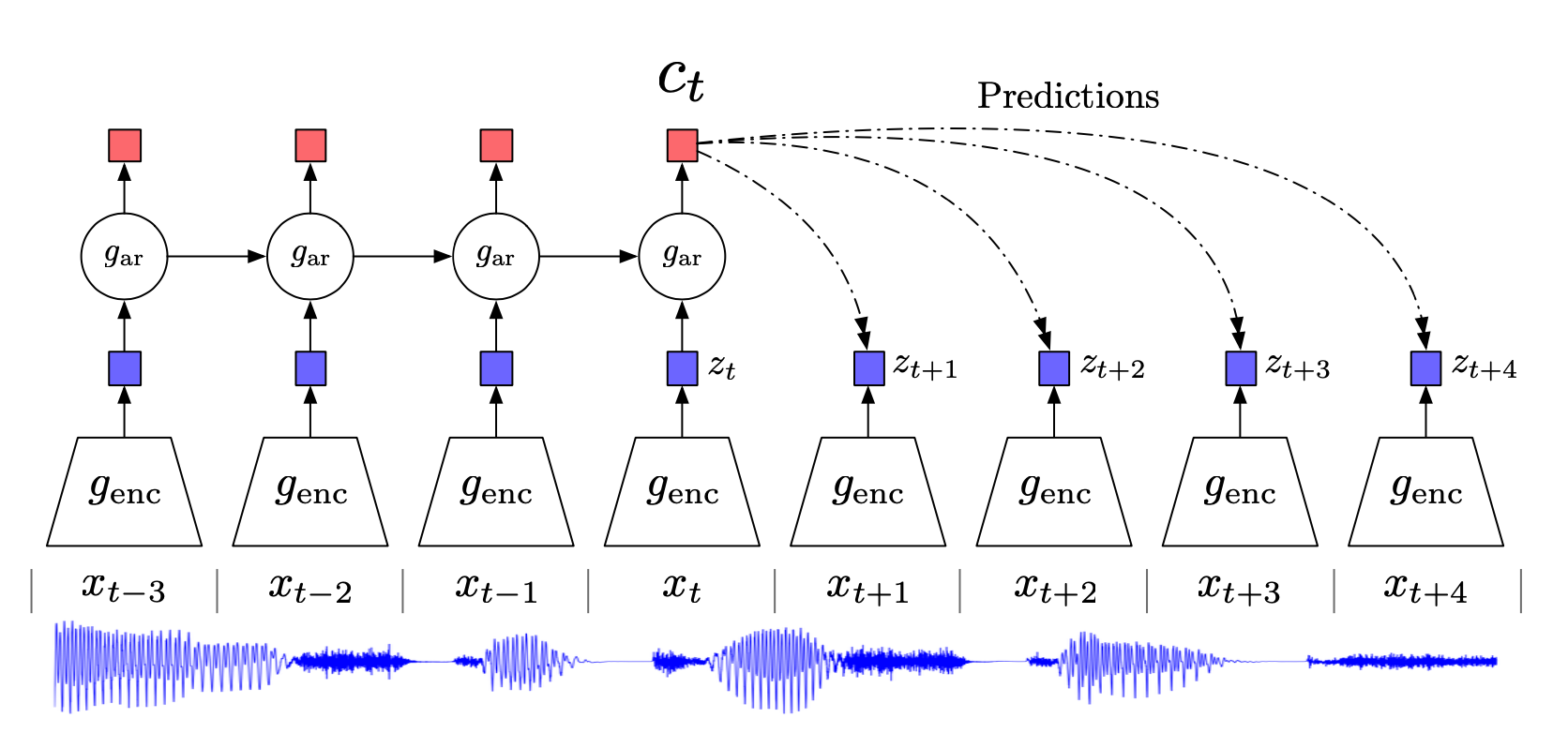
Self-Supervised
2026-01-23
如果把 近几年对比学习在视觉领域有代表性的工作做一下总结,那么对比学习的发展历程大概可以分为四个阶段: 百花齐放 这个阶段代表性工作有InstDisc(instance discrimination,)、CPC、CMC等。在这个阶段中,方法、模型、目标函数、代理任务都还没有统一,所以说是一个百花齐放的时代 CV双雄 代表作有MoCo v1、SimCLR v1、MoCo v2、SimCLR v2;CPC、CMC的延伸工作、SwAV等。这个阶段发展非常迅速,有的工作间隔甚至不到一个月,ImageNet上的成绩基本上每个月都在被刷新。 不用负样本 BYOL及其改进工作、SimSiam(CNN在对比学习中的总结性工作) transformer MoCo v3、DINO。这个阶段,无论是对比学习还是最新的掩码学习,都是用Vision Transformer做的。 第一阶段:百花齐放(2018-2019Mid) InstDisc(instance discrimination) 这篇文章提出了个体判别任务(代理任务)以及 memory bank ,非常经典,后人给它的方法起名为InstDisc。...