INCOMING TRANSMISSION

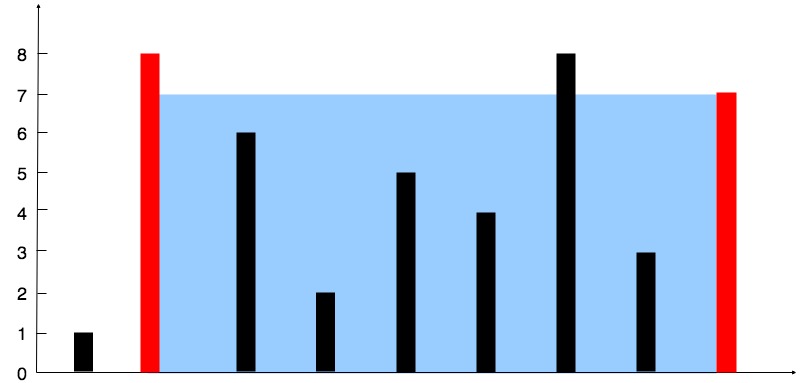
11. 盛最多水的容器 题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明： 你不能倾斜容器。 示例 1： 输入：[1,8,6,2,5,4,8,3,7] 输出：49 解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。 示例 2： 输入：height = [1,1] 输出：1 提示： n == height.length 2 <= n <= 10 5 0 <= height[i] <= 10 4 题解 在初始时，左右指针分别指向数组的左右两端，它们可以容纳的水量为 \(min(1,7)∗8=8\) 。 此时我们需要移动一个指针。移动哪一个呢？直觉告诉我们，应该移动对应数字较小的那个指针（即此时的左指针）。这是因为，由于容纳的水量是由 两个指针指向的数字中较小值∗指针之间的距离...

76. 最小覆盖子串 题目 给定两个字符串 s 和 t ，长度分别是 m 和 n ，返回 s 中的 最短窗口 子串 ，使得该子串包含 t 中的每一个字符（ 包括重复字符 ）。如果没有这样的子串，返回空字符串 "" 。 测试用例保证答案唯一。 示例 1： 输入：s = "ADOBECODEBANC", t = "ABC" 输出："BANC" 解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。 示例 2： 输入：s = "a", t = "a" 输出："a" 解释：整个字符串 s 是最小覆盖子串。 示例 3: 输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中， 因此没有符合条件的子字符串，返回空字符串。 提示： m == s.length n == t.length 1 <= m, n <= 10 5 s 和 t 由英文字母组成 题解 这是一个经典的 滑动窗口 (Sliding Window) 问题 我们需要维护一个动态的窗口 [left, right] ： 右移扩大 ：不断移动...

简介 如果以概率的视角看待世界的生成模型。 在这样的世界观中，我们可以将任何类型的观察数据（例如 \(D\) ）视为来自底层分布（例如 \( p_{data}\) ）的有限样本集。 任何生成模型的目标都是在访问数据集 \(D\) 的情况下近似该数据分布。 如果我们能够学习到一个好的生成模型，我们可以将学习到的模型用于下游推理。 我们主要对数据分布的参数近似感兴趣，在一组有限的参数中，它总结了关于数据集 \(D\) 的所有信息。 与非参数模型相比，参数模型在处理大型数据集时能够更有效地扩展，但受限于可以表示的分布族。 在参数的设置中，我们可以将学习生成模型的任务视为在模型分布族中挑选参数，以最小化模型分布和数据分布之间的距离。 如上图，给定一个狗的图像数据集，我们的目标是学习模型族 \(M\) 中生成模型 θ 的参数，使得模型分布 \(p_θ\) 接近 \(p_{data}\) 上的数据分布。 在数学上，我们可以将我们的目标指定为以下优化问题: \[\mathop{min}\limits_{\theta\in M}d(p_\theta,p_{data})\] 其中， \(d()\)...

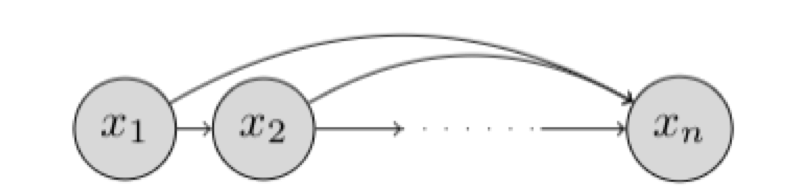
研究对象与基本设定 我们希望学习一个能够“生成数据”的概率模型。假设我们有一个数据集 \(D\) ，每个样本是 \(n\) 维二值向量： \(x \in \{0,1\}^n\) 我们的目标是用一个参数化分布 \(p_\theta(x)\) 去逼近真实数据分布 \(p_{\text{data}}(x)\) ，并最终能够： 密度估计 ：给定 \(x\) 计算 \(p_\theta(x)\) 或 \(\log p_\theta(x)\) 采样生成 ：从 \(p_\theta(x)\) 采样得到新的 \(x\) 表示：链式法则与自回归分解 链式法则分解联合分布 任意联合分布都可用概率链式法则分解为条件概率的乘积： \[p(x) = \prod_{i=1}^{n} p(x_i \mid x_1, x_2, \dots, x_{i-1}) = \prod_{i=1}^{n} p(x_i \mid x_{<i})\] 其中： \(x_{<i} = [x_1, x_2, \dots, x_{i-1}]\) ，这意味着：只要我们能为每个维度 \(i\) 学好一个条件分布 \(p(x_i \mid...

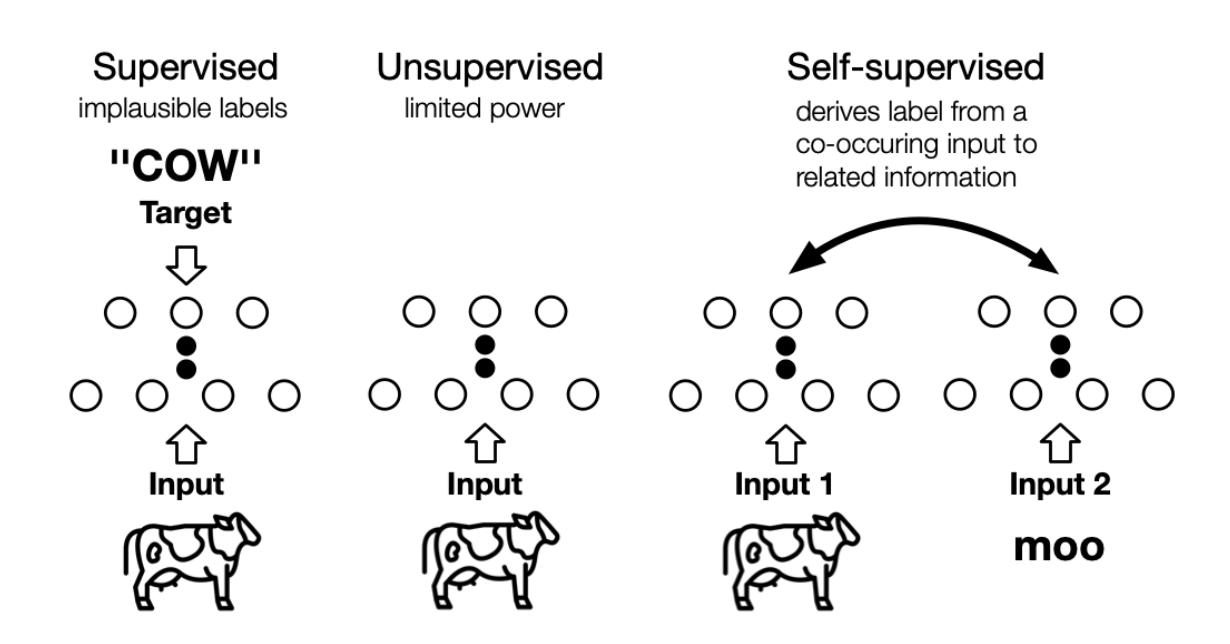
the machine predicts any parts of its input for any observed part 这是LeCun在AAAI 2020上对自监督学习的定义，再结合传统的自监督学习定义，可以总结如下两点特征： 通过“半自动”过程从数据本身获取“标签”； 从“其他部分”预测部分数据。 个人理解， 其实任意挖掘对象之间联系、探索不同对象共同本质的方法，都或多或少算是自监督学习的思想 。 自监督学习与无监督学习的区别主要在于，无监督学习专注于检测特定的数据模式，如聚类、社区发现或异常检测，而自监督学习的目标是恢复（recovering），仍处于监督学习的范式中。上图展示了三者之间的区别， 自监督中的“related information” 可以来自其他模态、输入的其他部分以及输入的不同形式。 Self-Supervised...

超多分类的Softmax 2014年CVPR两篇超多分类的人脸识别论文：DeepFace和DeepID DeepFace Taigman Y, Yang M, Ranzato M A, et al. Deepface: Closing the gap to humanlevel performance in face verification [C]// CVPR, 2014. 4.4M训练集，训练6层CNN + 4096特征映射 + 4030类Softmax，综合如3D Aligement, model ensembel等技术，在LFW上达到97.35%。 DeepID Sun Y, Wang X, Tang X. Deep learning face representation fro...

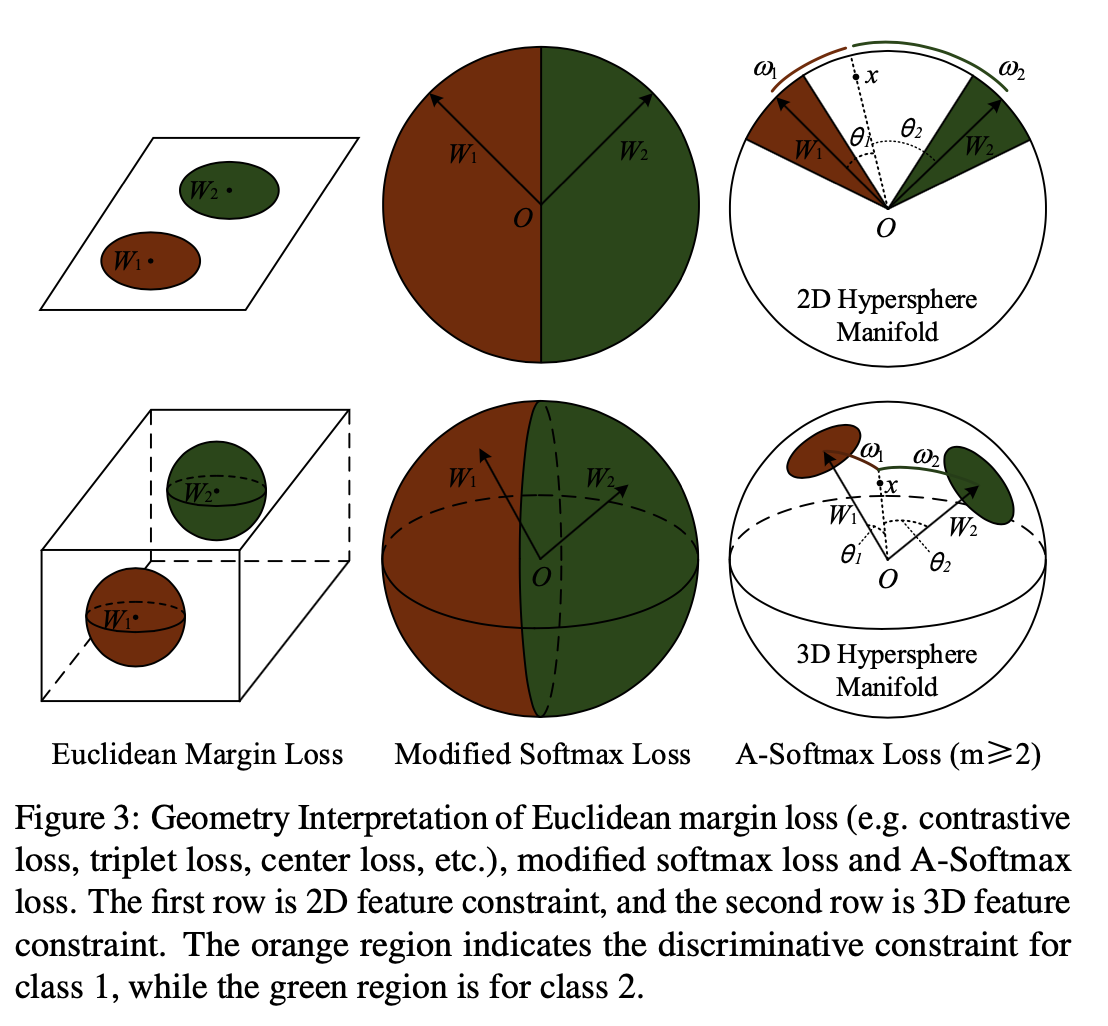
推导 回顾一下二分类下的Softmax后验概率，即： [公式] 显然决策的分界在当 𝑝_1=𝑝_2 时，所以决策界面是 (𝑊_1−𝑊_2)𝑥+𝑏_1−𝑏_2=0 。我们可以将 𝑊^𝑇_𝑖𝑥+𝑏_𝑖 写成 ‖W_i^T‖⋅‖x‖cos⁡(θ_i)+b_i ，其中 θ_i 是 W_i 与 x 的夹角，如对 W_i 归一化且设偏置 b_i 为零（ ‖W_i‖=1 ， b_i=0 ），那么当 p_1=p_2 时，我们有 cos⁡(θ_1)−cos⁡(θ_2)=0 。从这里可以看到，如里一个输入的数据特征 x_i 属于 𝑦_𝑖 类，那么 θ_{y_i} 应该比其它所有类的角度都要小，也就是说在向量空间中 W_{y_i} 要更靠近 x_i 。 我们用的是Softmax Loss，对于输入 x_i ，So...

给定一个包含 n 维数据 x 的数据集 D , 简单起见，假设数据 [Math] . 由于真正对联合分布建模的时候， x，y 都是随机变量，故而只需讨论 p(X)=p(x_1,...,x_n) 即可，毕竟只需要令 x_n=y 即可。 给定一个具体的任务，如MNIST中的手写数字二值图分类，从Generative的角度进行Represent，并在Inference中Learning. 下面先介绍： 描述如何对这个MINST任务建模 p(X,Y) （Representation） 对MNIST任务建模 对于一张pixel为 [Math] 大小的图片，令 x_1 表示第一个pixel的随机变量， [Math] ，需明确： 任务目标：学习一个模型分布 [Math] ，使采样时 [Math] ， x ...

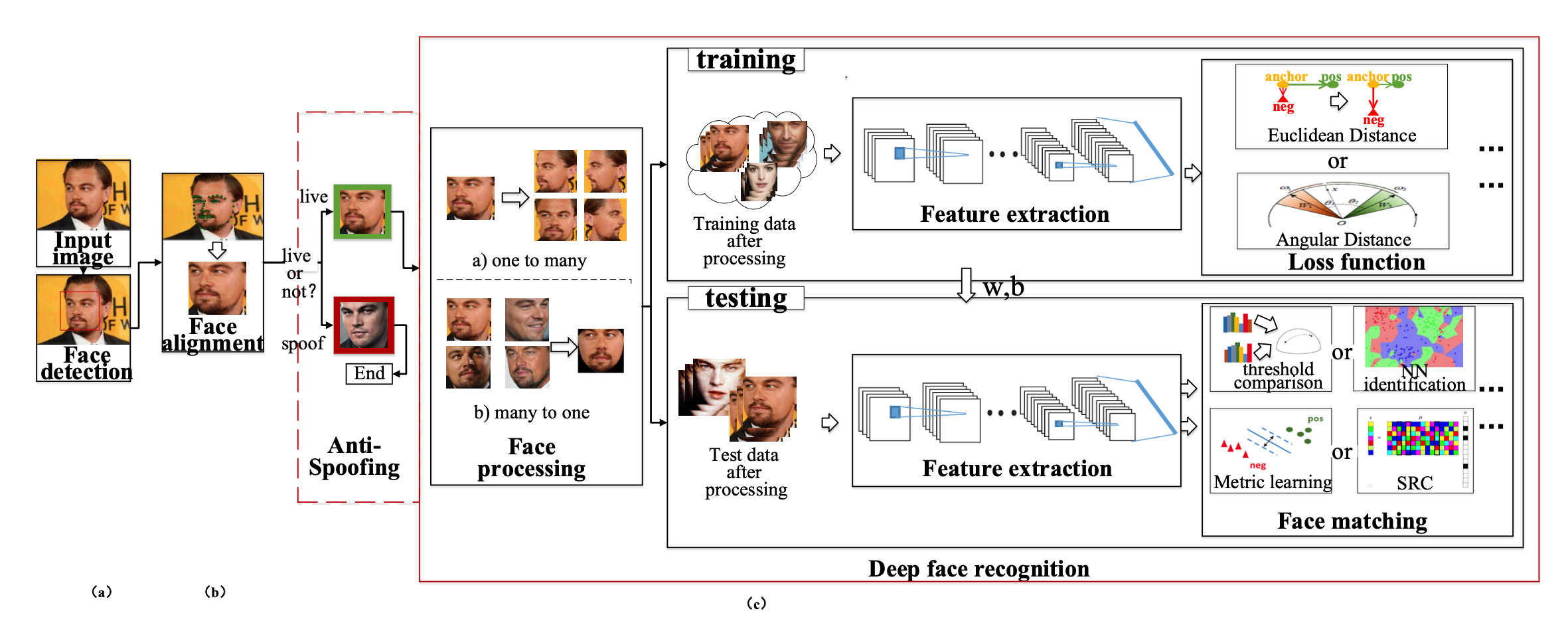
简介 一个完整的人脸识别系统包含以下几个模块 Face Detection: 人脸检测 Face Alignment：基于人脸关键点坐标对齐到正则坐标系下坐标 Face Recognition：基于对齐人脸进行识别 人脸识别的算法流程 人脸的识别流程：面部姿态处理(处理姿态，亮度，表情，遮挡)，特征提取，人脸比对。 面部处理 face processing 这部分主要对姿态（主要）、亮度、表情、遮挡进行处理，可提升FR模型性能 主要包含两种处理方式： 1. "Onetomany Augmentation": 从单个图像生成不同姿态的图像，使模型学习到姿态不变性的表示 1. "Manytoone Normalization": 从多个不同姿态的图像中恢复人脸图像的标准视图 特征提取 Backb...

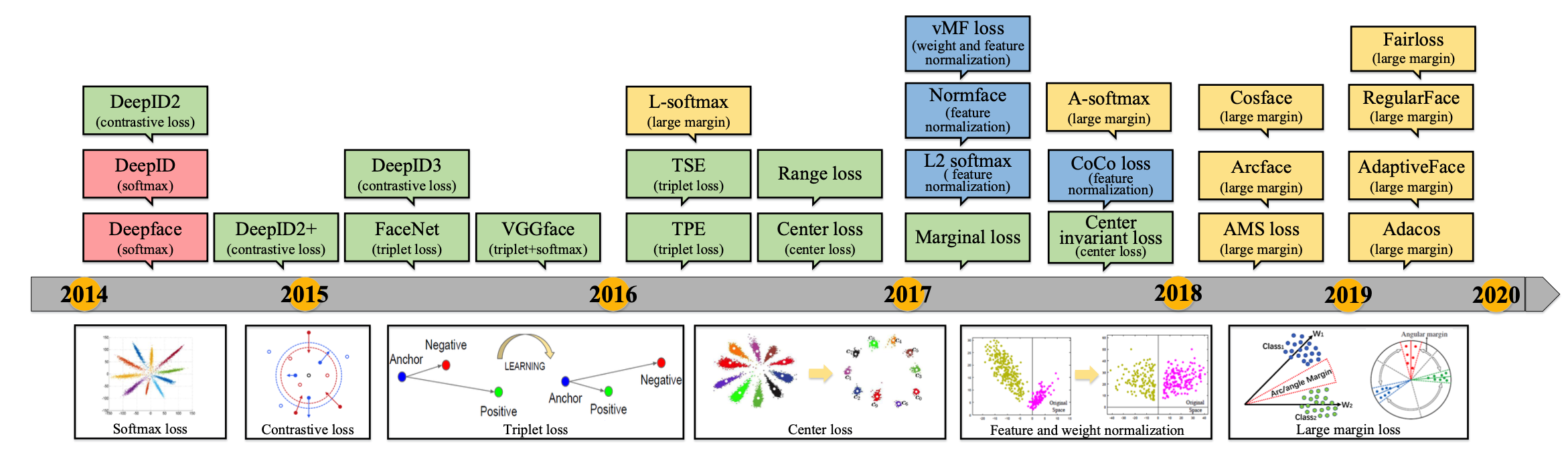
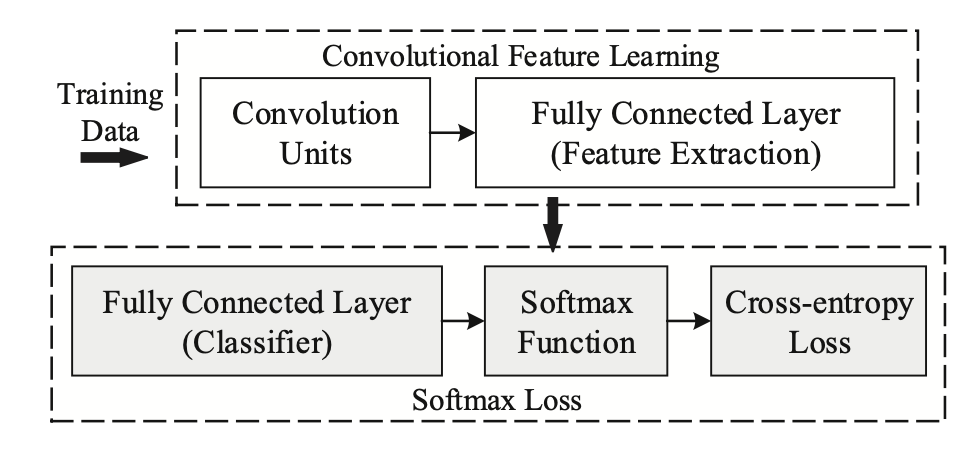
近期，人脸识别研究领域的主要进展之一集中在了 Softmax Loss 的改进之上；本文从两种主要的改进方式——做归一化以及增加类间 margin——展开梳理，介绍了近年来基于 Softmax 的 Loss 的研究进展。 Softmax简介 Softmax Loss 因为其易于优化，收敛快等特性被广泛应用于图像分类领域。然而，直接使用 softmax loss 训练得到的 feature 拿到 retrieval，verification 等“需要设阈值”的任务时，往往并不够好。 这其中的原因还得从 Softmax 的本身的定义说起，Softmax loss 在形式上是 softmax 函数加上交叉熵损失，它的目的是让所有的类别在概率空间具有最大的对数似然，也就是保证所有的类别都能分类正确，...