INCOMING TRANSMISSION

128. 最长连续序列 题目 给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 1： 输入：nums = [100,4,200,1,3,2] 输出：4 解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。 示例 2： 输入：nums = [0,3,7,2,5,8,4,6,0,1] 输出：9 示例 3： 输入：nums = [1,0,1,2] 输出：3 提示： 0 <= nums.length <= 10 5 -10 9 <= nums[i] <= 10 9 题解 我们需要在 \(O(1)\) 的时间内查找某个数是否存在。因此，首先将数组中的所有元素放入一个 HashSet 中。这不仅能去重，还能支持快速查找。 避免冗余计算 (关键优化) 如果我们对集合中的每一个数都尝试去向后计数（例如，对于 x ，尝试找 x+1 , x+2 ...），最坏情况下的时间复杂度会退化到 \(O(n^2)\) 。 优化策略 ： 我们 只从序列的起点开始计数 。...

76. 最小覆盖子串 题目 给定两个字符串 s 和 t ，长度分别是 m 和 n ，返回 s 中的 最短窗口 子串 ，使得该子串包含 t 中的每一个字符（ 包括重复字符 ）。如果没有这样的子串，返回空字符串 "" 。 测试用例保证答案唯一。 示例 1： 输入：s = "ADOBECODEBANC", t = "ABC" 输出："BANC" 解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。 示例 2： 输入：s = "a", t = "a" 输出："a" 解释：整个字符串 s 是最小覆盖子串。 示例 3: 输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中， 因此没有符合条件的子字符串，返回空字符串。 提示： m == s.length n == t.length 1 <= m, n <= 10 5 s 和 t 由英文字母组成 题解 这是一个经典的 滑动窗口 (Sliding Window) 问题 我们需要维护一个动态的窗口 [left, right] ： 右移扩大 ：不断移动...

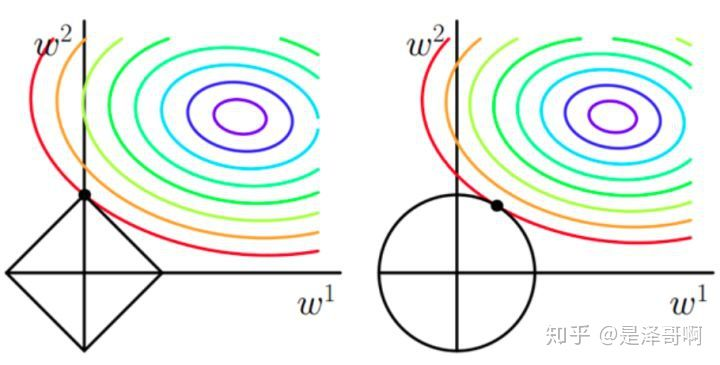
正则化 正则化是一个通用的算法和思想，所以会产生过拟合现象的算法都可以使用正则化来避免过拟合。 在经验风险最小化的基础上（也就是训练误差最小化），尽可能采用简单的模型，可以有效提高泛化预测精度。如果模型过于复杂，变量值稍微有点变动，就会引起预测精度问题。正则化之所以有效，就是因为其降低了特征的权重，使得模型更为简单。 正则化一般会采用 L1 范式或者 L2 范式，其形式分别为 [Math] 和 [Math] 。 L1正则化 LASSO 回归，相当于为模型添加了这样一个先验知识： w 服从零均值拉普拉斯分布。 首先看看拉普拉斯分布长什么样子： [公式] 由于引入了先验知识，所以似然函数这样写： [公式] 取 log 再取负，得到目标函数： [公式] 等价于原始损失函数的后面加上了 L1 正则，...

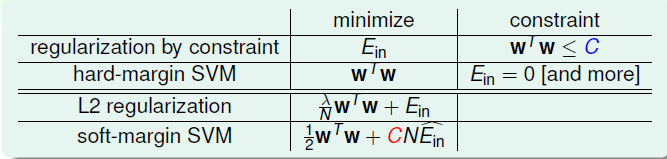
Kernel Logistic Regression 介绍如何将Kernel Trick引入到Logistic Regression，以及LR与SVM的结合 SVM与正则化 首先回顾SoftMargin SVM的原始问题: [公式] 其中 ξ_n 是训练数据违反边界的多少，没有违反的话， ξ_n=0 ，反之 ξ_n0 ，换句话说，目标函数的第二项就可以表示模型的损失。现在换一种方式来写，将二者结合起来: ξ_n=max(1−y_n(w^Tz^n+b),0) ，这一个等式就代表了上面的约束条件，这样上述问题，就与下面的无约束问题等价 [公式] 这种形式与之前的L2 正则项很类似: [公式] 在L2中，通过最小化 E_{in} 的同时控制 w 的大小，防止模型过度复杂。从正则化的角度来看的话，S...

EM算法也称期望最大化（ExpectationMaximum,简称EM）算法，它是一个基础算法，是很多机器学习领域算法的基础，比如隐式马尔科夫算法（HMM）， LDA主题模型的变分推断等等。本文就对EM算法的原理做一个总结。 EM算法要解决的问题 我们经常会从样本观察数据中，找出样本的模型参数。 最常用的方法就是极大化模型分布的对数似然函数。 但是在一些情况下，我们得到的观察数据有未观察到的隐含数据，此时我们未知的有隐含数据和模型参数，因而无法直接用极大化对数似然函数得到模型分布的参数。怎么办呢？这就是EM算法可以派上用场的地方了。 EM算法解决这个的思路是使用启发式的迭代方法，既然我们无法直接求出模型分布参数，那么我们可以先猜想隐含数据（EM算法的E步），接着基于观察数据和猜测的隐含数据一...

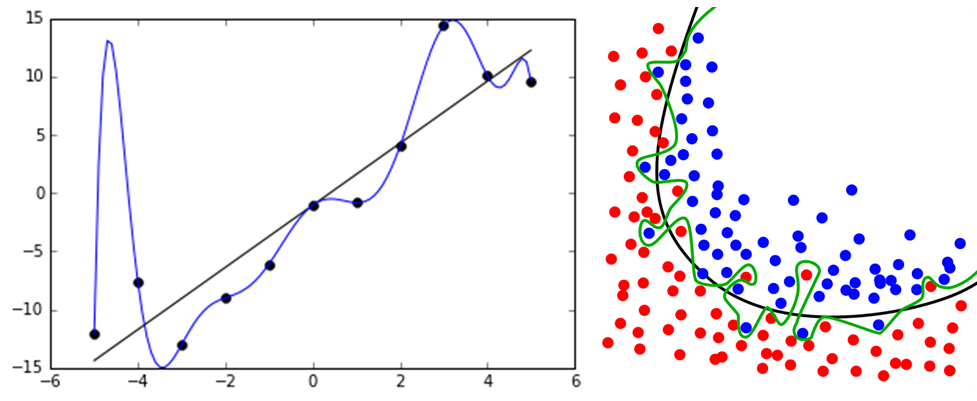
是什么 过拟合（overfitting）是指在模型参数拟合过程中的问题，由于训练数据包含抽样误差，训练时，复杂的模型将抽样误差也考虑在内，将抽样误差也进行了很好的拟合。 具体表现就是最终模型在训练集上效果好；在测试集上效果差。模型泛化能力弱。 为什么 为什么要解决过拟合现象？这是因为我们拟合的模型一般是用来预测未知的结果（不在训练集内），过拟合虽然在训练集上效果好，但是在实际使用时（测试集）效果差。同时，在很多问题上，我们无法穷尽所有状态，不可能将所有情况都包含在训练集上。所以，必须要解决过拟合问题。 为什么在机器学习中比较常见？这是因为机器学习算法为了满足尽可能复杂的任务，其模型的拟合能力一般远远高于问题复杂度，也就是说，机器学习算法有「拟合出正确规则的前提下，进一步拟合噪声」的能力。 而...

随机森林 (Random Forests) 是一种利用CART决策树作为基学习器的 Bagging 集成学习算法。随机森林模型的构建过程如下： 数据采样 作为一种 Bagging 集成算法，随机森林同样采用有放回的采样，对于总体训练集 T ，抽样一个子集 T_{sub} 作为训练样本集。除此之外，假设训练集的特征个数为 d ，每次仅选择 k(k<d) 个构建决策树。因此，随机森林除了能够做到样本扰动外，还添加了特征扰动，对于特征的选择个数，推荐值为 k=log_2⁡d 。 树的构建 每次根据采样得到的数据和特征构建一棵决策树。在构建决策树的过程中，会让决策树生长完全而不进行剪枝。构建出的若干棵决策树则组成了最终的随机森林。 随机森林在众多分类算法中表现十分出众，其主要的优点包括： 1. 由于...

AdaBoost基本思路 分类问题 Adaboost 是 Boosting 算法中有代表性的一个。原始的 Adaboost 算法用于解决二分类问题，因此对于一个训练集 [公式] 其中 [Math] ，，首先初始化训练集的权重 [公式] 根据每一轮训练集的权重 D_m ，对训练集数据进行抽样得到 T_m ，再根据 T_m 训练得到每一轮的基学习器 h_m 。通过计算可以得出基学习器 h_m 的误差为 e_m [公式] 根据基学习器的误差计算得出该基学习器在最终学习器中的权重系数 [公式] 为什么这样计算弱学习器权重系数？从上式可以看出，如果分类误差率 𝑒_𝑘 越大，则对应的弱分类器权重系数 [Math] 越小。也就是说，误差率小的弱分类器权重系数越大。具体为什么采用这个权重系数公式，见AdaB...

GBDT (Gradient Boosting Decision Tree) 是另一种基于 Boosting 思想的集成算法，除此之外 GBDT 还有很多其他的叫法，例如：GBM (Gradient Boosting Machine)，GBRT (Gradient Boosting Regression Tree)，MART (Multiple Additive Regression Tree) 等等。GBDT 算法由 3 个主要概念构成：Gradient Boosting (GB)，Regression Decision Tree (DT 或 RT) 和 Shrinkage。 0. Decision Tree：CART回归树 首先，GBDT使用的决策树是CART回归树，无论是处理回归问题还...

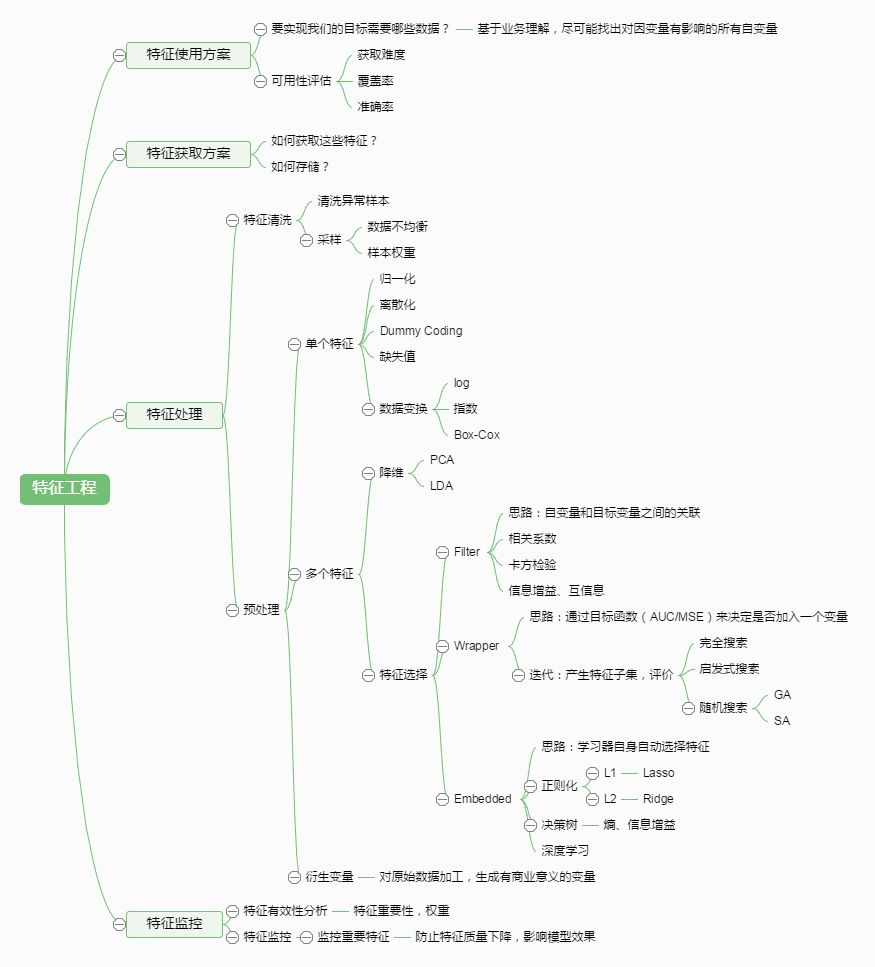
特征工程是什么？ 有这么一句话在业界广泛流传：数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已。那特征工程到底是什么呢？顾名思义，其本质是一项工程活动，目的是最大限度地从原始数据中提取特征以供算法和模型使用。通过总结和归纳，人们认为特征工程包括以下方面： 特征处理是特征工程的核心部分，sklearn提供了较为完整的特征处理方法，包括数据预处理，特征选择，降维等。首次接触到sklearn，通常会被其丰富且方便的算法模型库吸引，但是这里介绍的特征处理库也十分强大！ 本文中使用sklearn中的IRIS（鸢尾花）数据集来对特征处理功能进行说明。IRIS数据集由Fisher在1936年整理，包含4个特征（Sepal.Length（花萼长度）、Sepal.Width（花萼宽度）、Pet...

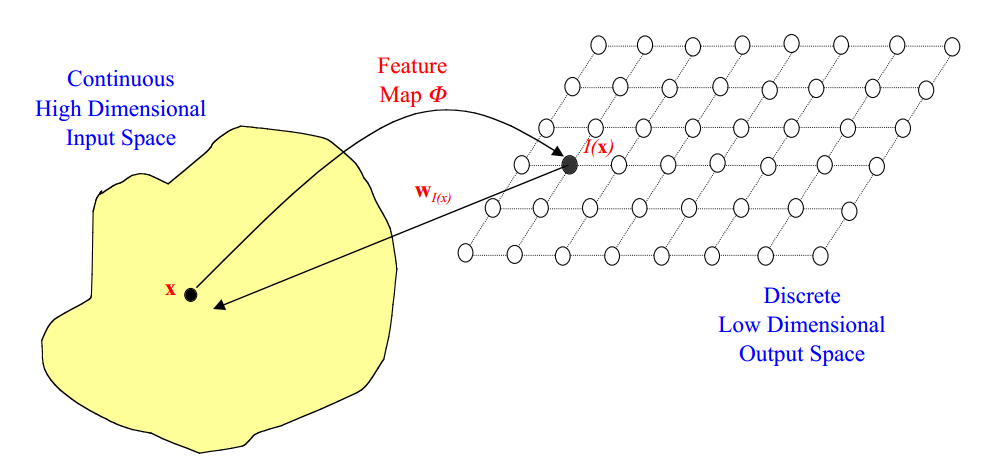
什么是自组织映射？ 一个特别有趣的无监督系统是基于竞争性学习，其中输出神经元之间竞争激活，结果是在任意时间只有一个神经元被激活。这个激活的神经元被称为胜者神经元（winnertakesall neuron）。这种竞争可以通过在神经元之间具有横向抑制连接（负反馈路径）来实现。其结果是神经元被迫对自身进行重新组合，这样的网络我们称之为自组织映射（Self Organizing Map，SOM）。 拓扑映射 神经生物学研究表明，不同的感觉输入（运动，视觉，听觉等）以有序的方式映射到大脑皮层的相应区域。 这种映射我们称之为拓扑映射，它具有两个重要特性： 在表示或处理的每个阶段，每一条传入的信息都保存在适当的上下文（相邻节点）中 处理密切相关的信息的神经元之间保持密切，以便它们可以通过短突触连接进行交...