INCOMING TRANSMISSION

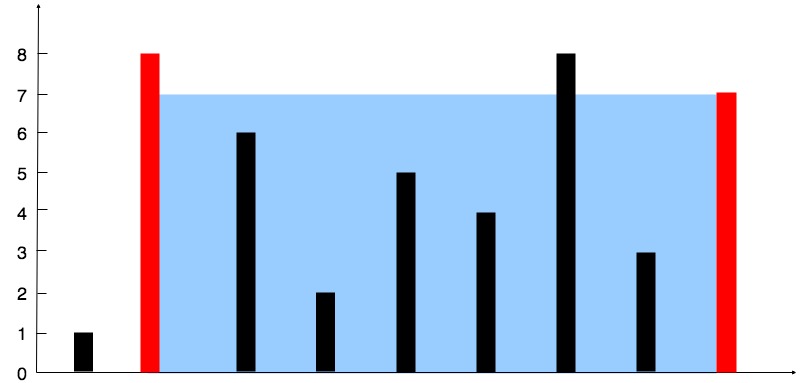
11. 盛最多水的容器 题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明： 你不能倾斜容器。 示例 1： 输入：[1,8,6,2,5,4,8,3,7] 输出：49 解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。 示例 2： 输入：height = [1,1] 输出：1 提示： n == height.length 2 <= n <= 10 5 0 <= height[i] <= 10 4 题解 在初始时，左右指针分别指向数组的左右两端，它们可以容纳的水量为 \(min(1,7)∗8=8\) 。 此时我们需要移动一个指针。移动哪一个呢？直觉告诉我们，应该移动对应数字较小的那个指针（即此时的左指针）。这是因为，由于容纳的水量是由 两个指针指向的数字中较小值∗指针之间的距离...

如果把 近几年对比学习在视觉领域有代表性的工作做一下总结，那么对比学习的发展历程大概可以分为四个阶段： 百花齐放 这个阶段代表性工作有InstDisc（instance discrimination，）、CPC、CMC等。在这个阶段中，方法、模型、目标函数、代理任务都还没有统一，所以说是一个百花齐放的时代 CV双雄 代表作有MoCo v1、SimCLR v1、MoCo v2、SimCLR v2；CPC、CMC的延伸工作、SwAV等。这个阶段发展非常迅速，有的工作间隔甚至不到一个月，ImageNet上的成绩基本上每个月都在被刷新。 不用负样本 BYOL及其改进工作、SimSiam（CNN在对比学习中的总结性工作） transformer MoCo v3、DINO。这个阶段，无论是对比学习还是最新的掩码学习，都是用Vision Transformer做的。 第一阶段：百花齐放（2018-2019Mid） InstDisc（instance discrimination） 这篇文章提出了个体判别任务（代理任务）以及 memory bank ，非常经典，后人给它的方法起名为InstDisc。...

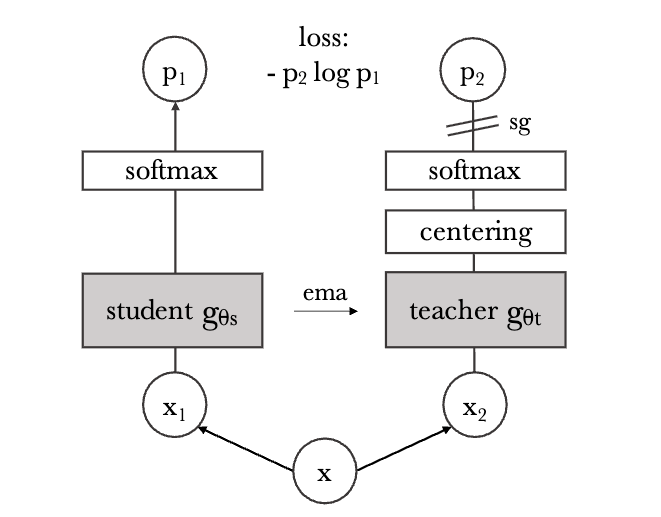
DINO Emerging Properties in Self-Supervised Vision Transformers 论文地址： arxiv.org/pdf/2104.14294 DINO摇摆到了动量式更新，果然【加动量】还是比【只用梯度停止】香。DINO的名字来自于Self- di stillation with no labels中的蒸馏和No标签。 DINO的训练步骤 其实以前的对比学习方案也可以理解为知识蒸馏，DINO里更具体得描述了知识蒸馏的含义。 下图展示了一个样本通过数据增强得到一对views \((x_1,x_2)\) 。注意DINO后面还会使用更复杂的裁剪和对比方案，但这里简单起见先不考虑那些。模型将输入图像的两种不同的随机变换 \(x_1\) 和 \(x_2\) 分别传递给学生和教师网络。 这两个网络具有相同的架构，但参数不同 。教师网络的输出以batch内计算的平均值，进行中心化（减去均值）。每个网络输出一个 \(K\)...

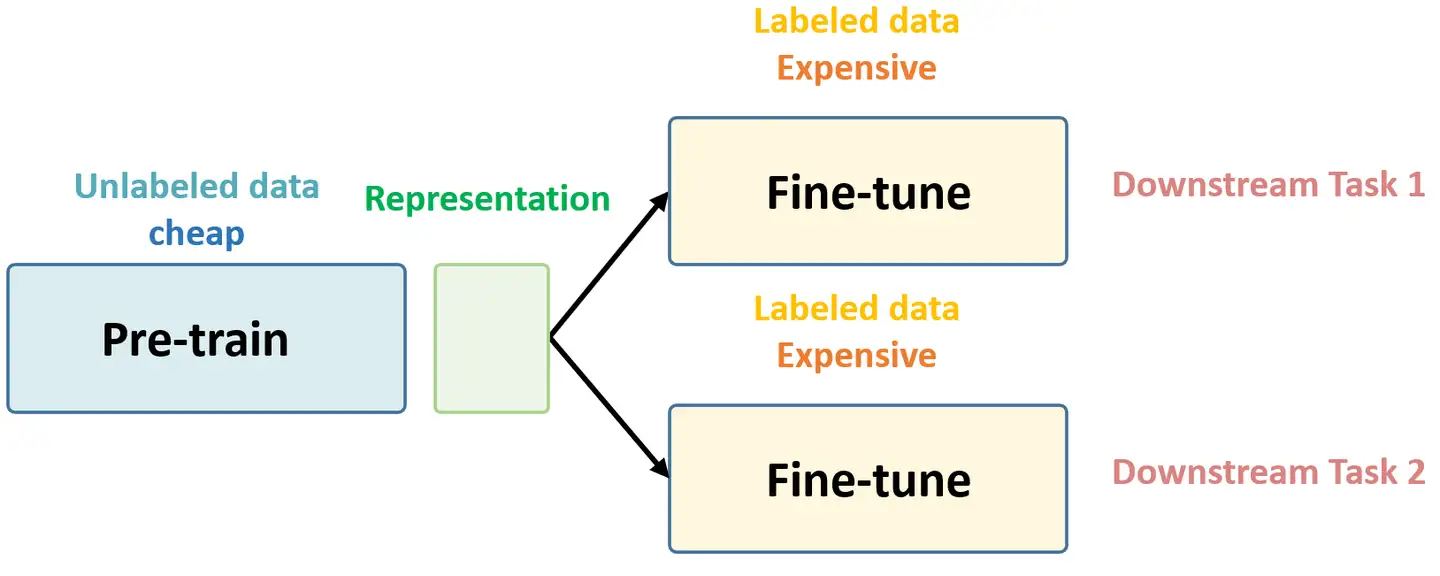
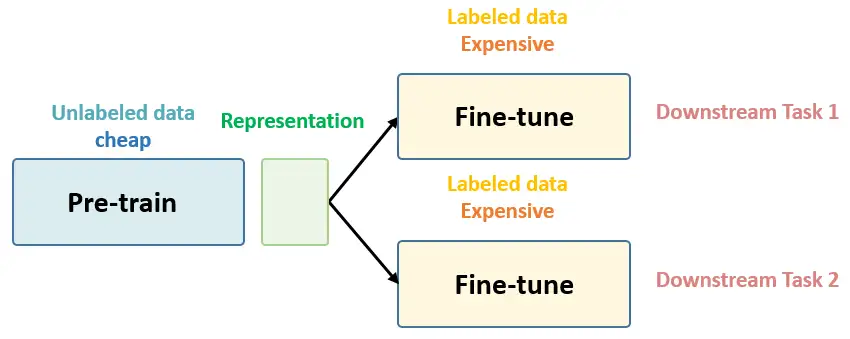
Self-Supervised Learning ，又称为自监督学习，我们知道一般机器学习分为有监督学习，无监督学习和强化学习。 而 Self-Supervised Learning 是无监督学习里面的一种，主要是希望能够学习到一种 通用的特征表达 用于 下游任务 (Downstream Tasks) 。 其主要的方式就是通过自己监督自己。作为代表作的 kaiming 的 MoCo 引发一波热议， Yann Lecun也在 AAAI 上讲 Self-Supervised Learning 是未来的大势所趋。所以在这个系列中，我会系统地解读 Self-Supervised Learning 的经典工作。 总结下 Self-Supervised Learning 的方法，用 4 个英文单词概括一下就是： Unsupervised Pre-train, Supervised Fine-tune. 这段话先放在这里，可能你现在还不一定完全理解，后面还会再次提到它。 在预训练阶段我们使用 无标签的数据集 (unlabeled data) ，因为有标签的数据集 很贵...

总结下 Self-Supervised Learning 的方法，用 4 个英文单词概括一下就是： Unsupervised Pre-train, Supervised Fine-tune. 在预训练阶段我们使用 无标签的数据集 (unlabeled data) ，因为有标签的数据集 很贵 ，打标签得要多少人工劳力去标注，那成本是相当高的，所以这玩意太贵。相反，无标签的数据集网上随便到处爬，它 便宜 。在训练模型参数的时候，我们不追求把这个参数用带标签数据从 初始化的一张白纸 给一步训练到位，原因就是数据集太贵。于是 Self-Supervised Learning 就想先把参数从 一张白纸 训练到 初步成型 ，再从 初步成型 训练到 完全成型 。注意这是2个阶段。这个 训练到初步成型的东西 ，我们把它叫做 Visual Representation 。预训练模型的时候，就是模型参数从 一张白纸 到 初步成型 的这个过程，还是用无标签数据集。等我把模型参数训练个八九不离十，这时候再根据你 下游任务 (Downstream Tasks) 的不同去用带标签的数据集把参数训练到 完全成型...

补充知识 表示学习 （Representation Learning）： 学习数据的表征，以便在构建分类器或其他预测器时更容易提取有用的信息 ，无监督学习也属于表示学习。 互信息 （Mutual Information）：表示两个变量 \(X\) 和 \(Y\) 之间的关系，定义为： \[I(X;Y)=\sum_{x\in X}\sum_{y\in Y}p(x,y)log\frac{p(x|y)}{p(x)}\] 对比损失(contrastive loss) ：计算成对样本的匹配程度，主要用于降维中。计算公式为： \[L=\frac{1}{2N}\sum_{n-1}^N[yd^2+(1-y)max(margin-d, 0)^2]\] 其中, \(d=\sqrt{(a_n-b_n)^2}\) 为两个样本的欧式距离， \(y=\{0,1\}\) 代表两个样本的匹配程度， \(margin\) 代表设定的阈值。这种损失函数可以很好的表达成对样本的匹配程度，也能够很好用于训练提取特征的模型。当 \( y=1\) （即样本相似）时，损失函数只剩下 \(∑d^2\)...

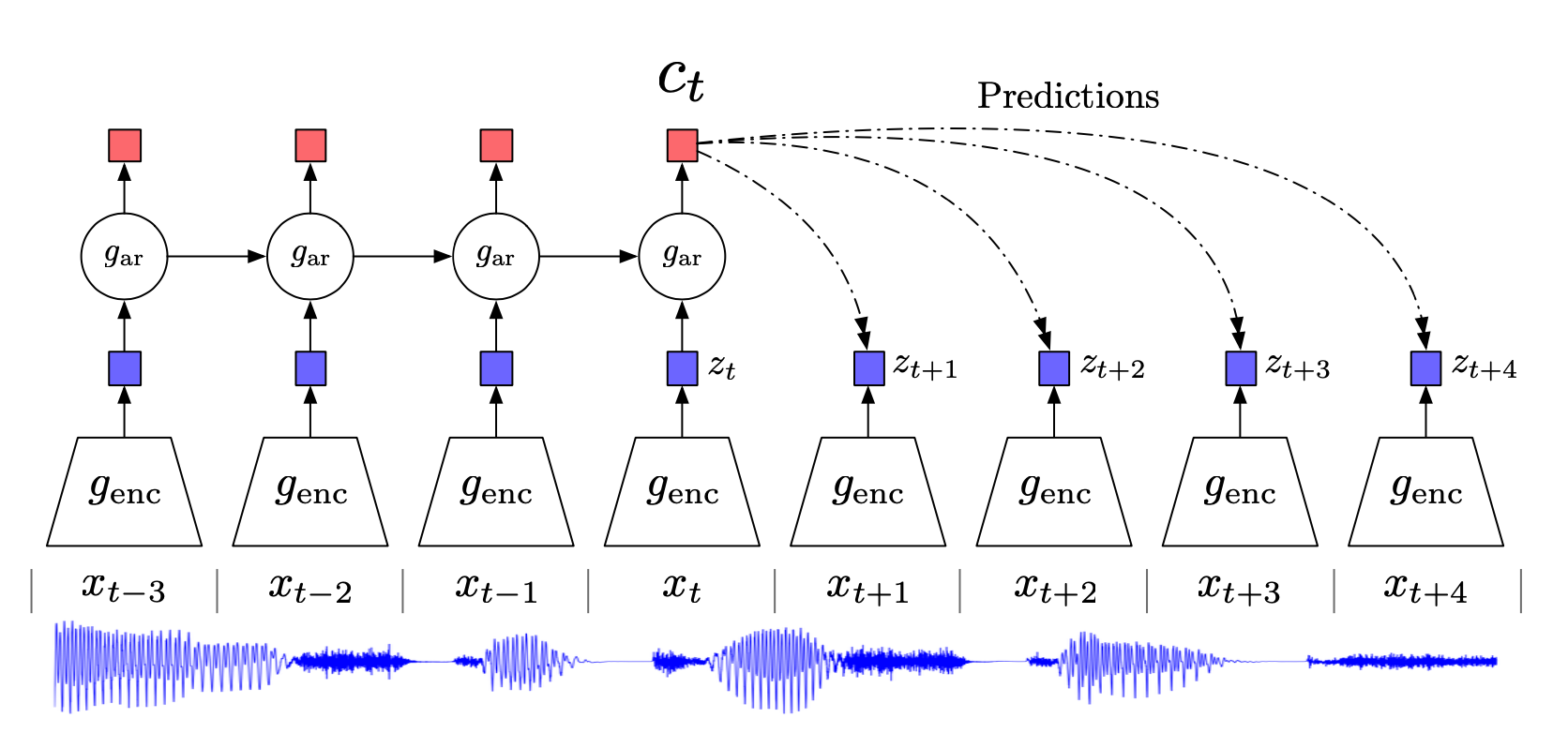
从 NLP 入手 n-gram 语言模型（language model）就是假设一门语言所有可能的句子服从一个概率分布，每个句子出现的概率加起来是1，那么语言模型的任务就是预测每个句子在语言中出现的概率。如果把句子 \(s\) 看成单词 \(w\) 的序列 \(s=\{w_1,w_2,...,w_m\}\) ，那么语言模型就是建模一个 \(p(w_1,w_2,...,w_m)\) 来计算这个句子 \(s\) 出现的概率，直观上我们要得到这个语言模型，基于链式法则可以表示为每个单词出现的条件概率的乘积，我们将条件概率的条件 \((w_1,w_2,...,w_{i-1})\) 称为单词 \(w_i\) 的上下文，用 \(c_i\) 表示。 \[\begin{aligned} p\left(w_{1}, w_{2}, \ldots, w_{m}\right)&=p\left(w_{1}\right) * p\left(w_{2} \mid w_{1}\right) * p\left(w_{3} \mid w_{1}, w_{2}\right) \ldots p\left(w_{m}...

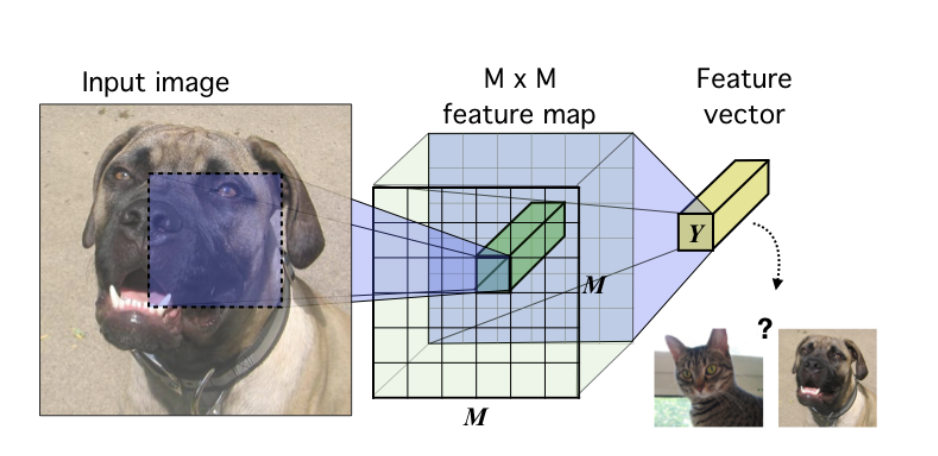
相关内容 自监督学习（Selfsupervised）：属于无监督学习，其核心是自动为数据打标签（伪标签或其他角度的可信标签，包括图像的旋转、分块等等），通过让网络按照既定的规则，对数据打出正确的标签来更好地进行特征表示，从而应用于各种下游任务。 互信息（Mutual Information）：表示两个变量 X 和 Y 之间的关系，定义为： 噪声对抗估计（Noise Contrastive Estimation, NCE）：在NLP任务中一种降低计算复杂度的方法，将语言模型估计问题简化为一个二分类问题。 Introduction 无监督学习一个重要的问题就是学习有用的 representation，本文的目的就是训练一个 representation learning 函数（即编码器encod...

问题表示 有很多概率问题，尤其是独立重复实验问题，如果用生成函数的方法来做，会显得特别方便。本文要讲的“随机游走”问题便是其中一例，它又被形象地叫做“醉汉问题”，其本质上是一个二项分布，但是由于取了极限，出现了很多新的性质和应用。我们先考虑如下问题： 考虑实数轴上的一个粒子，在 t=0 时刻它位于原点，每过一秒，它要不向前移动一格（+1），要不就向后移动一格（1），问 n 秒后它所处位置的概率分布。 不难发现，这个问题跟二项分布是雷同的。如果把这个粒子形象比喻成一个“喝醉酒的人”，那么上面的走法就类似于一个完全不省人事的醉汉走路问题了。（当然，醉汉是在三维空间走路的，这里简单起见，只描述了一维...

问题定义 多元二次多项式，维度为 n ，那么可以用以下公式描述该函数： [Formula] 其中 a_{i,j} 为二次项系数，共有 n^2 项， 1≤i,j≤n ，且所有的 a 不全为0，即 ∃a_{i,j}≠0 ; b_k 为一次项系数，共 n 项， 1≤k≤n ; c 为常数项。 记 f(x)=[x_1,x_2,...,x_n]^T ，则上述函数可以写作二次型的形式： 转化过程中A,b满足： A 为n阶对称方阵， A_{i,j}=a_{i,j} 因为 ∃a_{i,j}≠0 ，A不为零矩阵 b_i=b_i 为了后续计算简便，我们将二次型稍作改动： [Formula] 我们的目标就是寻找该函...

基本概念 方向导数：是一个数；反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 偏导数：是多个数（每元有一个）；是指多元函数沿坐标轴方向的方向导数，因此二元函数就有两个偏导数。 偏导函数：是一个函数；是一个关于点的偏导数的函数。 梯度：是一个向量；每个元素为函数对一元变量的偏导数；它既有大小（其大小为最大方向导数），也有方向。 方向导数 反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 例子如下： 题目 设二元函数 f(x, y) = x^2 + y^2 ，分别计算此函数在点 (1, 2) 沿方向 w=\{3, 4\} 与方向 u=\{1, 0\} 的方向导数。 解： ...

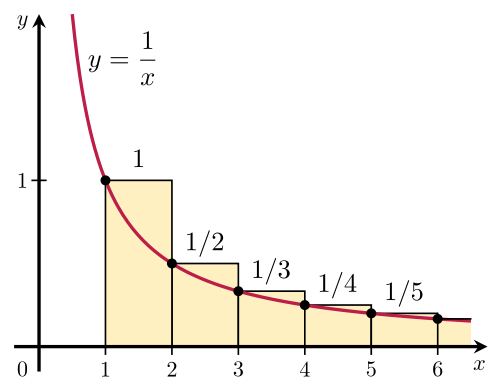
调和级数记住下面的公式就够了： [Formula] 证明方法就是下面这张图