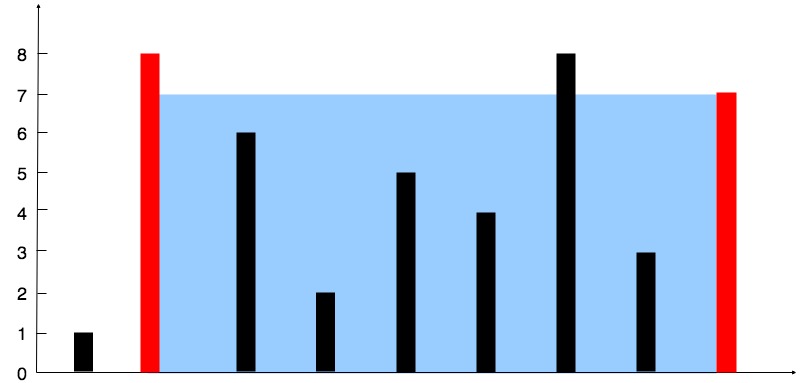
11. 盛最多水的容器 题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明: 你不能倾斜容器。 示例 1: 输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。 示例 2: 输入:height = [1,1]
输出:1 提示: n == height.length 2 <= n <= 10 5 0 <= height[i] <= 10 4 题解 在初始时,左右指针分别指向数组的左右两端,它们可以容纳的水量为 \(min(1,7)∗8=8\) 。 此时我们需要移动一个指针。移动哪一个呢?直觉告诉我们,应该移动对应数字较小的那个指针(即此时的左指针)。这是因为,由于容纳的水量是由 两个指针指向的数字中较小值∗指针之间的距离...
Generative Model
2026-01-19
基于文章 《Elucidating the Design Space of Diffusion-Based Generative Models》 来统一扩散模型框架 通用扩散模型框架推导 加噪公式 Flow Matching的一步加噪公式 \[\mathbf{x}_t=(1-t)\mathbf{x}_0+t\varepsilon\] 写成概率分布形式: \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;(1-t)\mathbf{x}_0,t^2\mathbf{I})\] Score Matching的一步加噪公式 \[\mathbf{x}_t=\mathbf{x}_0+\sigma_t\varepsilon \] 写成概率分布形式: \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;\mathbf{x}_0,\sigma_t^2\mathbf{I})\] DDPM/DDIM的一步加噪公式...
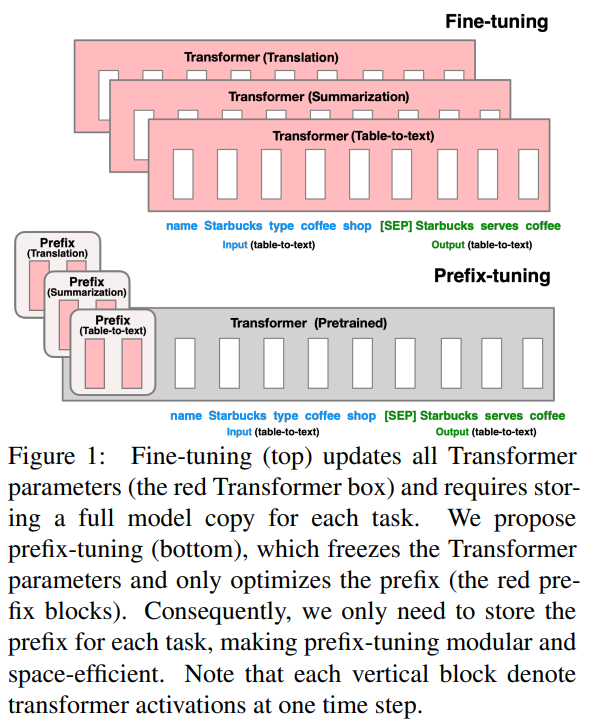
PrefixTuning Paper: 2021.1 Optimizing Continuous Prompts for GenerationGithub:https://github.com/XiangLi1999/PrefixTuningPrompt: Continus Prefix PromptTask & Model:BART(Summarization), GPT2(Table2Text) 最早提出Prompt微调的论文之一,其实是可控文本生成领域的延伸,因此只针对摘要和Table2Text这两个生成任务进行了评估。 PrefixTuning可以理解是CTRL模型的连续化升级版,为了生成不同领域和话题的文本,CTRL是在预训练阶段在输入文本前加入了control code,例如好评...
Large Model
2026-01-11
背景 随着预训练语言模型进入LLM时代,其参数量愈发庞大。全量微调模型所有参数所需的显存早已水涨船高。 例如: 全参微调Qwen1.57BChat预估要2张80GB的A800,160GB显存 全参微调Qwen1.572BChat预估要20张80GB的A800,至少1600GB显存。 而且,通常不同的下游任务还需要LLM的全量参数,对于算法服务部署来说简直是个灾难 当然,一种折衷做法就是全量微调后把增量参数进行SVD分解保存,推理时再合并参数 为了寻求一个不更新全部参数的廉价微调方案,之前一些预训练语言模型的高效微调(Parameter Efficient finetuning, PEFT)工作,要么插入一些参数或学习外部模块来适应新的下游任务。 Adapter tuning Adapter ...
Generative Model
2026-01-11
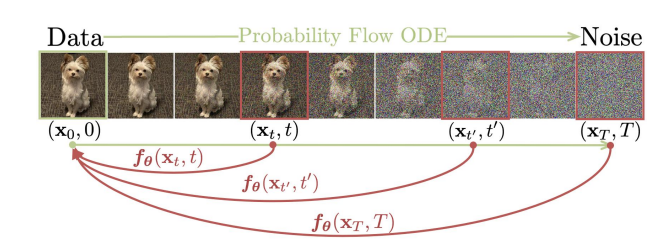
Diffusion Models from SDE 连续扩散模型 (Continuous Diffusion Models) 将传统的离散时间扩散过程扩展到连续时间域,可以被视为一个随机过程,使用随机微分方程(SDE)来描述。其前向过程可以写成如下形式: [公式] 其中, f(x,t) 可以看成偏移系数, g(t) 可以看成是扩散系数, dw 是标准布朗运动。这个SDE 描述了数据在连续时间域内如何被噪声逐渐破坏。 这个随机过程的逆向过程存在(更准确的描述:下面的逆向时间SDE具有与正向过程SDE相同的联合分布)为 [公式] 前面我们得到了扩散过程的逆向过程可以用一个SDE描述(逆向随机过程),事实上,存在一个确定性过程 (用ODE描述)也是它的逆向过程 (更准确的描述:这个ODE过程的在任...
Generative Model
2026-01-11
💡 Score based generative model SMLD的关键点: 正式开始介绍之前首先解答一下这个问题:scorebased 模型是什么东西,微分方程在这个模型里到底有什么用?我们知道生成模型基本都是从某个现有的分布中进行采样得到生成的样本,为此模型需要完成对分布的建模。根据建模方式的不同可以分为隐式建模(例如 GAN、diffusion models)和显式建模(例如 VAE、normalizing flows)。和上述的模型相同,scorebased 模型也是用一定方式对分布进行了建模。具体而言,这类模型建模的对象是概率分布函数 log 的梯度,也就是 score function,而为了对这个建模对象进行学习,需要使用一种叫做 score matching 的技术,这也...
Large Model
2026-01-11
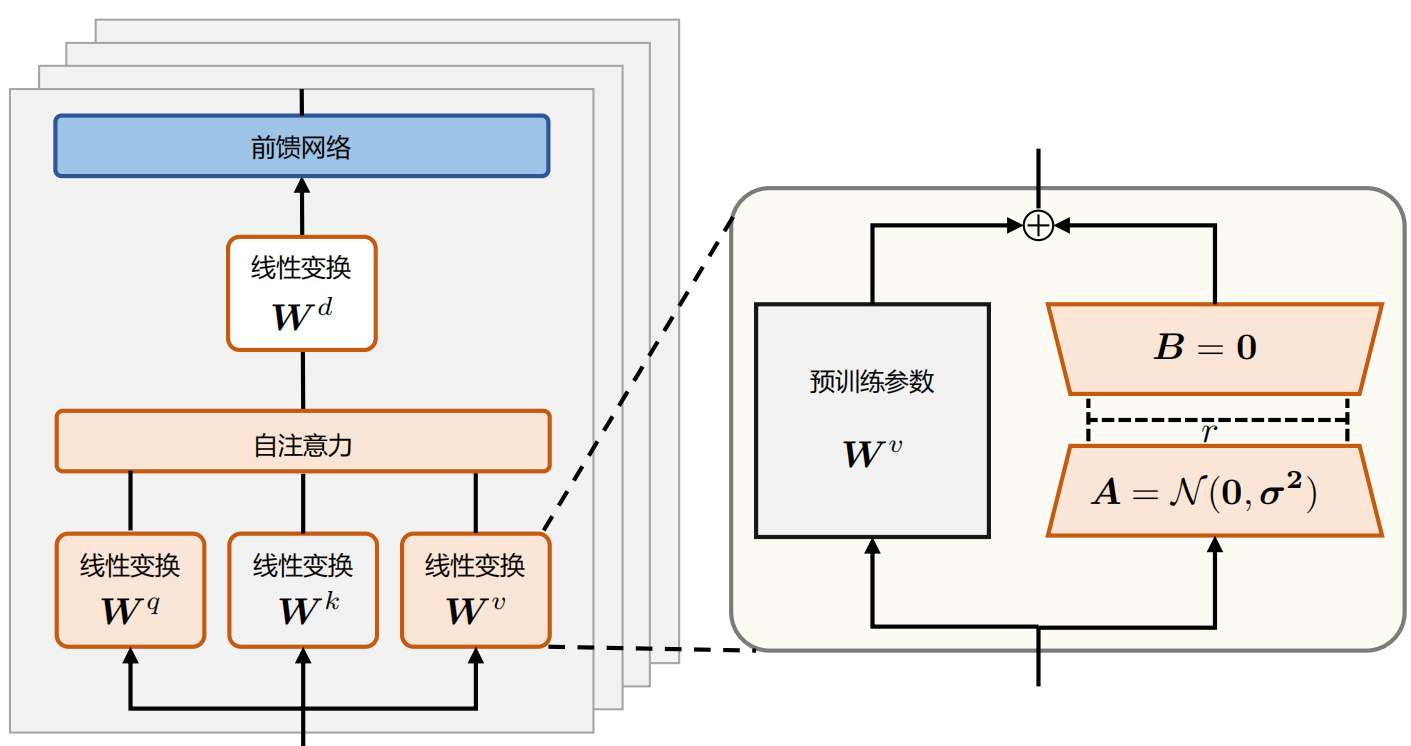
背景 随着预训练语言模型进入LLM时代,其参数量愈发庞大。全量微调模型所有参数所需的显存早已水涨船高。 例如: 全参微调Qwen1.57BChat预估要2张80GB的A800,160GB显存 全参微调Qwen1.572BChat预估要20张80GB的A800,至少1600GB显存。 而且,通常不同的下游任务还需要LLM的全量参数,对于算法服务部署来说简直是个灾难 当然,一种折衷做法就是全量微调后把增量参数进行SVD分解保存,推理时再合并参数 为了寻求一个不更新全部参数的廉价微调方案,之前一些预训练语言模型的高效微调(Parameter Efficient finetuning, PEFT)工作,要么插入一些参数或学习外部模块来适应新的下游任务。 LoRA LoRA(LowRank Adapt...
Generative Model
2026-01-11
💡 随机微分 在DDPM中,扩散过程被划分为了固定的T步,还是用DDPM中的类比来说,就是“拆楼”和“建楼”都被事先划分为了T步,这个划分有着相当大的人为性。事实上,真实的“拆”、“建”过程应该是没有刻意划分的步骤的,我们可以将它们理解为一个在时间上连续的变换过程,可以用随机微分方程(Stochastic Differential Equation,SDE)来描述。 为此,我们用下述SDE描述前向过程(“拆楼”): [公式] 相信很多读者都对SDE很陌生,笔者也只是在硕士阶段刚好接触过一段时间,略懂皮毛。不过不懂不要紧,我们只需要将它看成是下述离散形式在 [Math] 时的极限: [公式] 再直白一点,如果假设拆楼需要1天,那么拆楼就是 [Math] 从 t=0 到 t=1 的变化过程,每一...