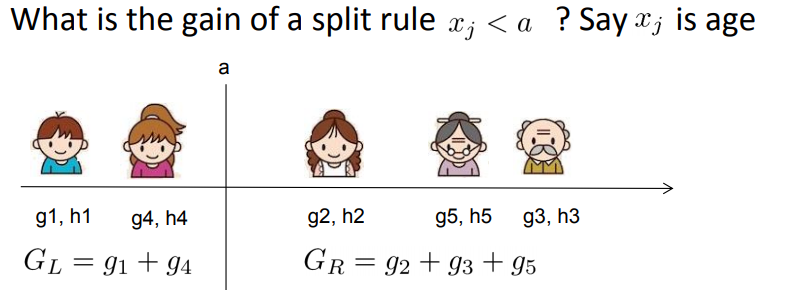INCOMING TRANSMISSION

129. 滑动窗口最大值 题目 给你一个整数数组 nums ，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 示例 1： 输入：nums = [1,3,-1,-3,5,3,6,7], k = 3 输出：[3,3,5,5,6,7] 解释： 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7 示例 2： 输入：nums = [1], k = 1 输出：[1] 提示： 1 <= nums.length...

随机森林 (Random Forests) 是一种利用CART决策树作为基学习器的 Bagging 集成学习算法。随机森林模型的构建过程如下： 数据采样 作为一种 Bagging 集成算法，随机森林同样采用有放回的采样，对于总体训练集 T ，抽样一个子集 T_{sub} 作为训练样本集。除此之外，假设训练集的特征个数为 d ，每次仅选择 k(k<d) 个构建决策树。因此，随机森林除了能够做到样本扰动外，还添加了特征扰动，对于特征的选择个数，推荐值为 k=log_2⁡d 。 树的构建 每次根据采样得到的数据和特征构建一棵决策树。在构建决策树的过程中，会让决策树生长完全而不进行剪枝。构建出的若干棵决策树则组成了最终的随机森林。 随机森林在众多分类算法中表现十分出众，其主要的优点包括： 1. 由于...

AdaBoost基本思路 分类问题 Adaboost 是 Boosting 算法中有代表性的一个。原始的 Adaboost 算法用于解决二分类问题，因此对于一个训练集 [公式] 其中 [Math] ，，首先初始化训练集的权重 [公式] 根据每一轮训练集的权重 D_m ，对训练集数据进行抽样得到 T_m ，再根据 T_m 训练得到每一轮的基学习器 h_m 。通过计算可以得出基学习器 h_m 的误差为 e_m [公式] 根据基学习器的误差计算得出该基学习器在最终学习器中的权重系数 [公式] 为什么这样计算弱学习器权重系数？从上式可以看出，如果分类误差率 𝑒_𝑘 越大，则对应的弱分类器权重系数 [Math] 越小。也就是说，误差率小的弱分类器权重系数越大。具体为什么采用这个权重系数公式，见AdaB...

GBDT (Gradient Boosting Decision Tree) 是另一种基于 Boosting 思想的集成算法，除此之外 GBDT 还有很多其他的叫法，例如：GBM (Gradient Boosting Machine)，GBRT (Gradient Boosting Regression Tree)，MART (Multiple Additive Regression Tree) 等等。GBDT 算法由 3 个主要概念构成：Gradient Boosting (GB)，Regression Decision Tree (DT 或 RT) 和 Shrinkage。 0. Decision Tree：CART回归树 首先，GBDT使用的决策树是CART回归树，无论是处理回归问题还...

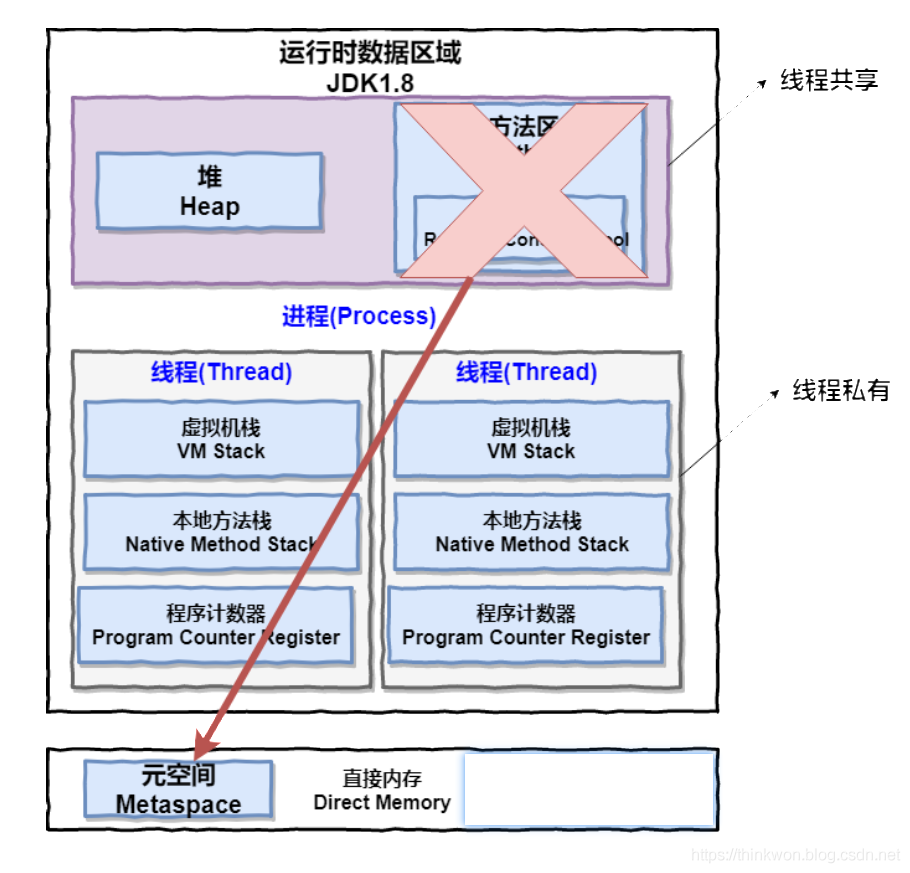
进程 一个在内存中运行的应用程序。每个进程都有自己独立的一块内存空间，一个进程可以有多个线程，比如在Windows系统中，一个运行的xx.exe就是一个进程。 线程 进程中的一个执行任务（控制单元），负责当前进程中程序的执行。一个进程至少有一个线程，一个进程可以运行多个线程，多个线程可共享数据。 与进程不同的是同类的多个线程共享进程的堆和方法区资源，但每个线程有自己的程序计数器、虚拟机栈和本地方法栈，所以系统在产生一个线程，或是在各个线程之间作切换工作时，负担要比进程小得多，也正因为如此，线程也被称为轻量级进程。 Java 程序天生就是多线程程序，我们可以通过 JMX 来看一下一个普通的 Java 程序有哪些线程，代码如下。 [代码] 上述程序输出如下（输出内容可能不同，不用太纠结下面每个线...

1. 从GBDT到XGBoost 作为GBDT的高效实现，XGBoost是一个上限特别高的算法，因此在算法竞赛中比较受欢迎。简单来说，对比原算法GBDT，XGBoost主要从下面三个方面做了优化： 一是算法本身的优化：在算法的弱学习器模型选择上，对比GBDT只支持决策树，还可以选择很多其他的弱学习器。在算法的损失函数上，除了本身的损失，还加上了正则化部分。在算法的优化方式上，GBDT的损失函数只对误差部分做负梯度（一阶泰勒）展开，而XGBoost损失函数对误差部分做二阶泰勒展开，更加准确。算法本身的优化是我们后面讨论的重点。 二是算法运行效率的优化：对每个弱学习器，比如决策树建立的过程做并行选择，找到合适的子树分裂特征和特征值。在并行选择之前，先对所有的特征的值进行排序分组，方便前面说的并行...

问题表示 有很多概率问题，尤其是独立重复实验问题，如果用生成函数的方法来做，会显得特别方便。本文要讲的“随机游走”问题便是其中一例，它又被形象地叫做“醉汉问题”，其本质上是一个二项分布，但是由于取了极限，出现了很多新的性质和应用。我们先考虑如下问题： 考虑实数轴上的一个粒子，在 t=0 时刻它位于原点，每过一秒，它要不向前移动一格（+1），要不就向后移动一格（1），问 n 秒后它所处位置的概率分布。 不难发现，这个问题跟二项分布是雷同的。如果把这个粒子形象比喻成一个“喝醉酒的人”，那么上面的走法就类似于一个完全不省人事的醉汉走路问题了。（当然，醉汉是在三维空间走路的，这里简单起见，只描述了一维...

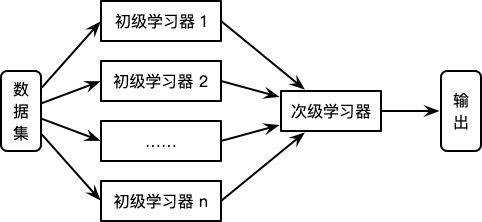
这篇博客介绍一下集成学习的几类：Bagging，Boosting以及Stacking。 传统机器学习算法 (例如：决策树，人工神经网络，支持向量机，朴素贝叶斯等) 的目标都是寻找一个最优分类器尽可能的将训练数据分开。集成学习 (Ensemble Learning) 算法的基本思想就是将多个分类器组合，从而实现一个预测效果更好的集成分类器。集成算法可以说从一方面验证了中国的一句老话：三个臭皮匠，赛过诸葛亮。 Thomas G. Dietterich 指出了集成算法在统计，计算和表示上的有效原因： 统计上的原因 一个学习算法可以理解为在一个假设空间 H 中选找到一个最好的假设。但是，当训练样本的数据量小到不够用来精确的学习到目标假设时，学习算法可以找到很多满足训练样本的分类器。所以，学习算法选择...

问题定义 多元二次多项式，维度为 n ，那么可以用以下公式描述该函数： [Formula] 其中 a_{i,j} 为二次项系数，共有 n^2 项， 1≤i,j≤n ，且所有的 a 不全为0，即 ∃a_{i,j}≠0 ; b_k 为一次项系数，共 n 项， 1≤k≤n ; c 为常数项。 记 f(x)=[x_1,x_2,...,x_n]^T ，则上述函数可以写作二次型的形式： 转化过程中A,b满足： A 为n阶对称方阵， A_{i,j}=a_{i,j} 因为 ∃a_{i,j}≠0 ，A不为零矩阵 b_i=b_i 为了后续计算简便，我们将二次型稍作改动： [Formula] 我们的目标就是寻找该函...

基本概念 方向导数：是一个数；反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 偏导数：是多个数（每元有一个）；是指多元函数沿坐标轴方向的方向导数，因此二元函数就有两个偏导数。 偏导函数：是一个函数；是一个关于点的偏导数的函数。 梯度：是一个向量；每个元素为函数对一元变量的偏导数；它既有大小（其大小为最大方向导数），也有方向。 方向导数 反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 例子如下： 题目 设二元函数 f(x, y) = x^2 + y^2 ，分别计算此函数在点 (1, 2) 沿方向 w=\{3, 4\} 与方向 u=\{1, 0\} 的方向导数。 解： ...

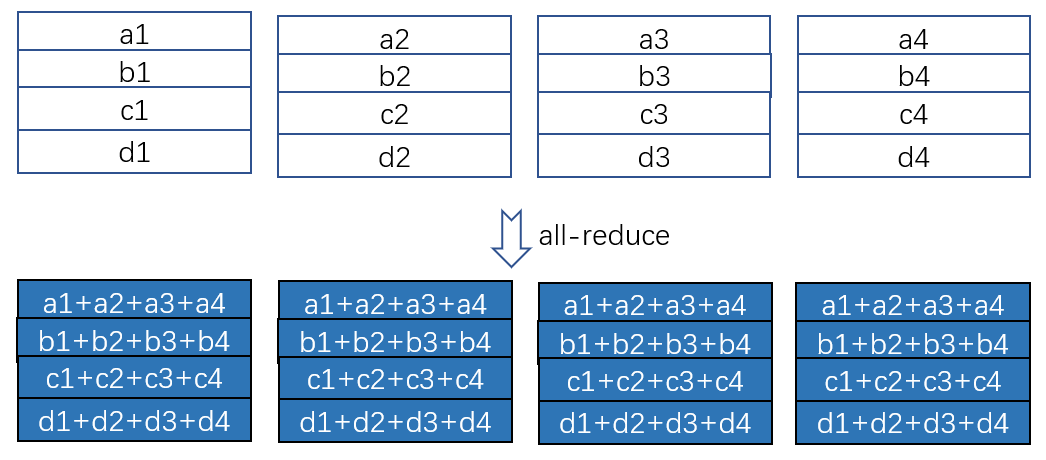
分布式深度学习里的通信严重依赖于规则的集群通信，诸如 allreduce, reducescatter, allgather 等，因此，实现高度优化的集群通信，以及根据任务特点和通信拓扑选择合适的集群通信算法至关重要。 本文以数据并行经常使用的 allreduce 为例来展示集群通信操作的数学性质。 Allreduce 在干什么？ 如图 1 所示，一共 4个设备，每个设备上有一个矩阵（为简单起见，我们特意让每一行就一个元素），allreduce 操作的目的是，让每个设备上的矩阵里的每一个位置的数值都是所有设备上对应位置的数值之和。 如图 2 所示， allreduce 可以通过 reducescatter 和 allgather 这两个更基本的集群通信操作来实现。基于 ring 状通信可以高...

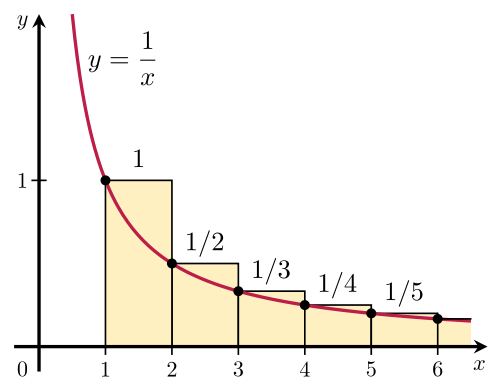
调和级数记住下面的公式就够了： [Formula] 证明方法就是下面这张图