INCOMING TRANSMISSION

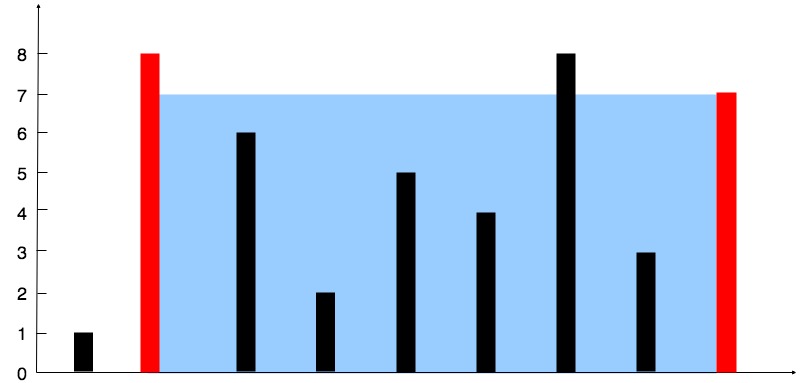
11. 盛最多水的容器 题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明： 你不能倾斜容器。 示例 1： 输入：[1,8,6,2,5,4,8,3,7] 输出：49 解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。 示例 2： 输入：height = [1,1] 输出：1 提示： n == height.length 2 <= n <= 10 5 0 <= height[i] <= 10 4 题解 在初始时，左右指针分别指向数组的左右两端，它们可以容纳的水量为 \(min(1,7)∗8=8\) 。 此时我们需要移动一个指针。移动哪一个呢？直觉告诉我们，应该移动对应数字较小的那个指针（即此时的左指针）。这是因为，由于容纳的水量是由 两个指针指向的数字中较小值∗指针之间的距离...

129. 滑动窗口最大值 题目 给你一个整数数组 nums ，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 示例 1： 输入：nums = [1,3,-1,-3,5,3,6,7], k = 3 输出：[3,3,5,5,6,7] 解释： 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7 示例 2： 输入：nums = [1], k = 1 输出：[1] 提示： 1 <= nums.length...

大数据本身是个很宽泛的概念，Hadoop生态圈(或者泛生态圈)基本上都是为了处理超过单机尺度的数据处理而诞生的。你可以把它比作一个厨房所以需要的各种工具。锅碗瓢盆，各有各的用处，互相之间又有重合。你可以用汤锅直接当碗吃饭喝汤，你可以用小刀或者刨子去皮。但是每个工具有自己的特性，虽然奇怪的组合也能工作，但是未必是最佳选择。 大数据，首先你要能存的下大数据 传统的文件系统是单机的，不能横跨不同的机器。HDFS(Hadoop Distributed FileSystem)的设计本质上是为了大量的数据能横跨成百上千台机器，但是你看到的是一个文件系统而不是很多文件系统。比如你说我要获取/hdfs/tmp/file1的数据，你引用的是一个文件路径，但是实际的数据存放在很多不同的机器上。你作为用户，不需要...

1. explode hive wiki对于expolde的解释如下： explode() takes in an array (or a map) as an input and outputs the elements of the array (map) as separate rows. UDTFs can be used in the SELECT expression list and as a part of LATERAL VIEW. As an example of using explode() in the SELECT expression list, consider a table named myTable that has a single column (m...

问题表示 有很多概率问题，尤其是独立重复实验问题，如果用生成函数的方法来做，会显得特别方便。本文要讲的“随机游走”问题便是其中一例，它又被形象地叫做“醉汉问题”，其本质上是一个二项分布，但是由于取了极限，出现了很多新的性质和应用。我们先考虑如下问题： 考虑实数轴上的一个粒子，在 t=0 时刻它位于原点，每过一秒，它要不向前移动一格（+1），要不就向后移动一格（1），问 n 秒后它所处位置的概率分布。 不难发现，这个问题跟二项分布是雷同的。如果把这个粒子形象比喻成一个“喝醉酒的人”，那么上面的走法就类似于一个完全不省人事的醉汉走路问题了。（当然，醉汉是在三维空间走路的，这里简单起见，只描述了一维...

问题定义 多元二次多项式，维度为 n ，那么可以用以下公式描述该函数： [Formula] 其中 a_{i,j} 为二次项系数，共有 n^2 项， 1≤i,j≤n ，且所有的 a 不全为0，即 ∃a_{i,j}≠0 ; b_k 为一次项系数，共 n 项， 1≤k≤n ; c 为常数项。 记 f(x)=[x_1,x_2,...,x_n]^T ，则上述函数可以写作二次型的形式： 转化过程中A,b满足： A 为n阶对称方阵， A_{i,j}=a_{i,j} 因为 ∃a_{i,j}≠0 ，A不为零矩阵 b_i=b_i 为了后续计算简便，我们将二次型稍作改动： [Formula] 我们的目标就是寻找该函...

基本概念 方向导数：是一个数；反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 偏导数：是多个数（每元有一个）；是指多元函数沿坐标轴方向的方向导数，因此二元函数就有两个偏导数。 偏导函数：是一个函数；是一个关于点的偏导数的函数。 梯度：是一个向量；每个元素为函数对一元变量的偏导数；它既有大小（其大小为最大方向导数），也有方向。 方向导数 反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 例子如下： 题目 设二元函数 f(x, y) = x^2 + y^2 ，分别计算此函数在点 (1, 2) 沿方向 w=\{3, 4\} 与方向 u=\{1, 0\} 的方向导数。 解： ...

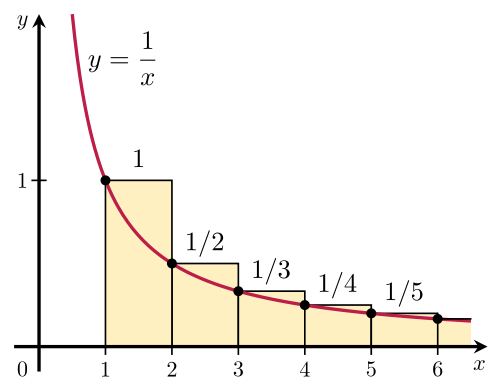
调和级数记住下面的公式就够了： [Formula] 证明方法就是下面这张图

一、泊松分布 日常生活中，大量事件是有固定频率的。 某医院平均每小时出生3个婴儿 某公司平均每10分钟接到1个电话 某超市平均每天销售4包xx牌奶粉 某网站平均每分钟有2次访问 它们的特点就是，我们可以预估这些事件的总数，但是没法知道具体的发生时间。已知平均每小时出生3个婴儿，请问下一个小时，会出生几个？ 有可能一下子出生6个，也有可能一个都不出生。这是我们没法知道的。 泊松分布就是描述某段时间内，事件具体的发生概率。 [Formula] 上面就是泊松分布的公式。等号的左边， P 表示概率， N 表示某种函数关系， t 表示时间， n 表示数量，1小时内出生3个婴儿的概率，就表示为 P(N(1...

概述 HiPPO（Highorder Polynomial Projection Operators）是目前大热的structured state space model (S4)及其后续工作的backbone. State space mode主要是控制学科里的内容，最近被引入深度学习领域来解决长距离依赖问题。长距离依赖建模的核心问题是如何通过有限的memory来尽可能记住之前所有的历史信息。当前的主流序列建模模型（即Transformer和RNN) 存在着普遍的遗忘问题 fixedsize context windows: Transformer的window size通常是有限的，一般来说quadratic的attention最多建模到大约10k的token就到计算极限了 vanish...

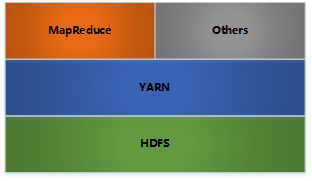
Apache Hadoop 是一款支持数据密集型分布式应用程序并以Apache 2.0许可协议发布的开源软件框架。它支持在商用硬件构建的大型集群上运行的应用程序。Hadoop是根据谷歌公司发表的MapReduce 和Google文件系统的论文自行实现而成。所有的Hadoop模块都有一个基本假设，即硬件故障是常见情况，应该由框架自动处理。具体参考官方教程。 Hadoop架构 HDFS: 分布式文件存储 YARN: 分布式资源管理 MapReduce: 分布式计算 Others: 利用YARN的资源管理功能实现其他的数据处理方式 内部各个节点基本都是采用MasterWoker架构 Hadoop HDFS 架构 Block数据块; NameNode Secondary NameNode DataN...