INCOMING TRANSMISSION

160. 相交链表 题目 给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。 图示两个链表在节点 c1 开始相交 ： 题目数据 保证 整个链式结构中不存在环。 注意 ，函数返回结果后，链表必须 保持其原始结构 。 自定义评测： 评测系统 的输入如下（你设计的程序 不适用 此输入）： intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0 listA - 第一个链表 listB - 第二个链表 skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数 skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数 评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。 示例 1： 输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2,...

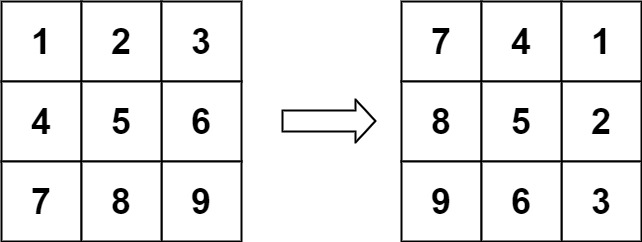
48. 旋转图像 题目 给定一个 \(n × n\) 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。 请不要 使用另一个矩阵来旋转图像。 示例 1： 输入：matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出：[[7,4,1],[8,5,2],[9,6,3]] 示例 2： 输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]] 提示： n == matrix.length == matrix[i].length 1 <= n <= 20 -1000 <= matrix[i][j] <= 1000 题解 这是一个经典的矩阵操作问题。要在原地（In-place）将图像顺时针旋转 90 度，我们可以利用矩阵的几何性质。 最直观且易于实现的方法是将...

数组&链表&字符串 双指针 滑动窗口 哈希表 哈希表 栈&队列 单调队列 树与堆 图 数学 Math

简介 生成树（spanning tree） 在图论中，无向图 G=(V,E) 的生成树（spanning tree)是具有G的全部顶点，但边数最少的联通子图。假设G中一共有n个顶点，一颗生成树满足下列条件： （1）n个顶点； （2）n1条边； （3）n个顶点联通； （4）一个图的生成树可能有多个。最小生成树（minimum spanning tree， MST）/最小生成森林：联通加权无向图中边缘权重加和最小的生成树。给定无向图 G=(V,E) ， (u,v) 代表顶点 u 与顶点 v 的边， w(u,v) 代表此边的权重，若存在生成树T使得： [公式] 最小，则 T 为 G 的最小生成树。对于非连通无向图来说，它的每一连通分量同样有最小生成树，它们的并被称为最小生成森林。最小生成树除了继承...

给一个无向图，判断其是否为一棵树。如果是树的话，所有的节点必须是连接的，也就是说必须是连通图，而且不能有环，所以就变成了验证是否是连通图和是否含有环。 [代码]

题目 中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。 例如， [2,3,4] 的中位数是 3 [2,3] 的中位数是 (2 + 3) / 2 = 2.5 设计一个支持以下两种操作的数据结构： void addNum(int num) 从数据流中添加一个整数到数据结构中。 double findMedian() 返回目前所有元素的中位数。 示例： addNum(1) addNum(2) findMedian() 1.5 addNum(3) findMedian() 2 题解 维护两个堆：大顶堆和小顶堆。并且需满足如下条件： 小顶堆的所有元素都大于等于大顶堆的所有元素。 大顶堆中的元素数量大于等于小顶堆中的元素数量。 大顶堆对应排序后的列表的左半部分；小顶堆对应排序...

[代码] 自己实现小顶堆 [代码] 变态的需求来了：给出N长的序列，求出BtmK小的元素，即使用大顶堆。 概括一种最简单的： 将push(e)改为push(e)、pop(e)改为pop(e)。 也就是说，在存入堆、从堆中取出的时候，都用相反数，而其他逻辑与TopK完全相同，看代码： [代码] 自己实现大顶堆 [代码]

二叉树结构 [代码] 递归 时间复杂度：O(n)，n为节点数，访问每个节点恰好一次。 空间复杂度：空间复杂度：O(h)，h为树的高度。最坏情况下需要空间O(n)，平均情况为O(logn) 递归1: 二叉树遍历最易理解和实现版本 [代码] 递归2: 通用模板 可以适应不同的题目，添加参数、增加返回条件、修改进入递归条件、自定义返回值 [代码] 迭代 时间复杂度：O(n)，n为节点数，访问每个节点恰好一次。 空间复杂度：O(h)，h为树的高度。取决于树的结构，最坏情况存储整棵树，即O(n) 迭代1: 前序遍历最常用模板（后序同样可以用） [代码] 迭代2: 前、中、后序遍历通用模板（只需一个栈的空间） [代码] 迭代3：标记法迭代（需要双倍的空间来存储访问状态） 前、中、后、层序通用模板，只需改...

Temporal action detection可以分为两种setting， 一是offline的，在检测时视频是完整可得的，也就是可以利用完整的视频检测动作发生的时间区间（开始时间+结束时间）以及动作的类别; 二是 online的，即处理的是一个视频流，需要在线的检测（or 预测未来）发生的动作类别，但无法知道检测时间点之后的内容。online的问题设定更符合surveillance的需求，需要做实时的检测或者预警；offline的设定更符合视频搜索的需求，比如youtube可能用到的 highlight detection / preview generation。 问题演化 Early action detection Online action detection Online a...

背包问题

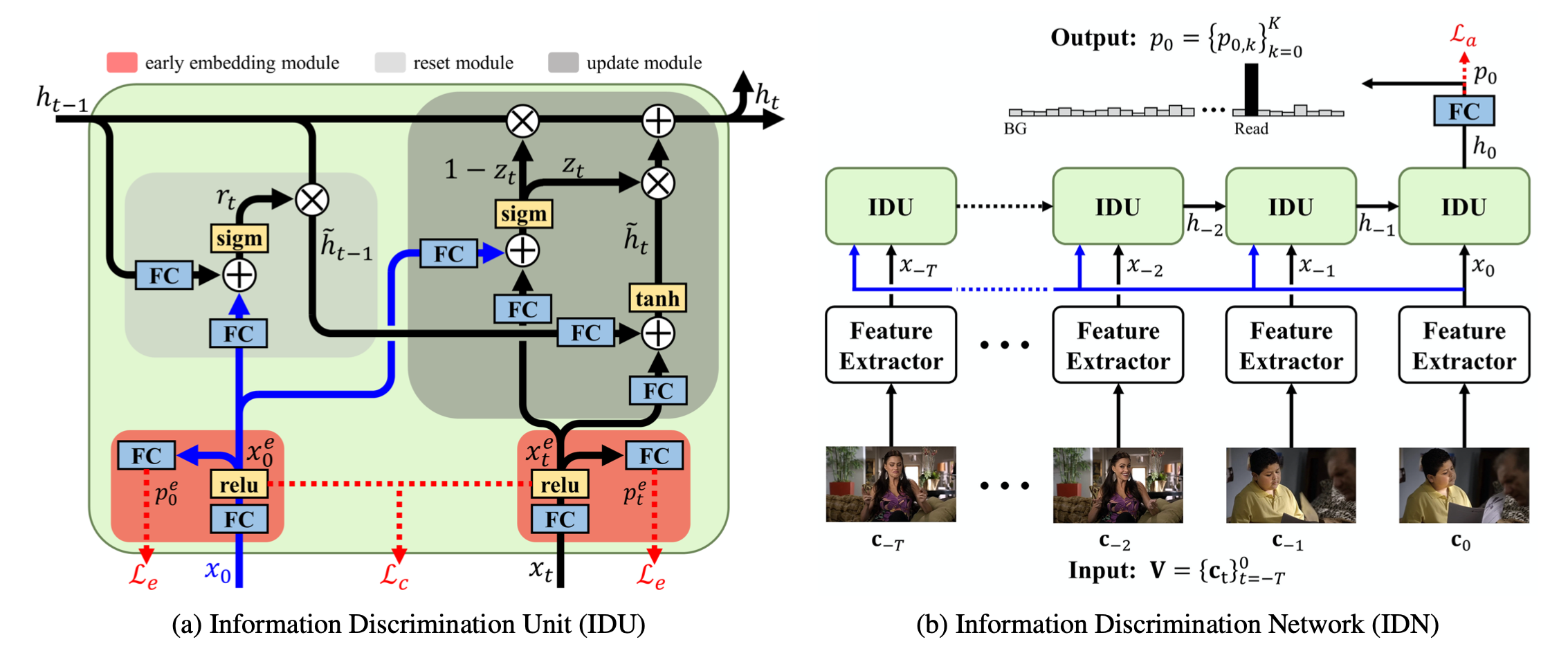
简介 这篇文章的思路就是之前的工作都是在利用历史信息和当前时刻的信息，而这篇文章就是要预测未来的信息来结合历史信息做分类。整体框架采用的lstm。 方法 传统的RNN或者LSTM并不能接收未来的信息，所以作者设计了一个TRN Cell为一个循环单元，TRN Cell 的算法流程如下： 右侧的可以横过来看，输入是大lstm中的隐状态h（文中把大的lstm称作Encoder），以h为输入再经过小的lstm，将输出连接起来构成future信息。 再解释一下就是，endcoder中得到了时间t的信息，那以t的信息为输入，再经过序列lstm，每个输出就可以看作是对未来 t+1...t+l_d 的预测，这些预测再经过一个FC层和 t 时刻的结合起来，作用于encoder的下一时序。 从Loss的角度来说...

简介 这篇文章主要的动机是，之前的RNN，LSTM，GRU这样的循环结构中，循环单元累计历史输入，但忽视了其与当前动作的联系，所以不能得到一个有效的判别性的表示。 Specifically, the recurrent unit accumulates the input information without explicitly considering its relevance to the current action, and thus the learned representation would be less discriminative. 所以， 这篇文章就是在探索是否可以学习一个判别性较强的表示区分相关和不相关的信息以检测当前要动作。 how RNNs can lear...