INCOMING TRANSMISSION

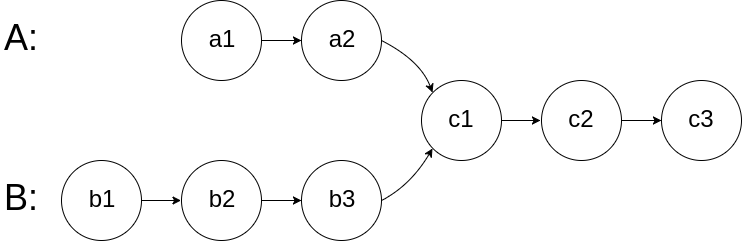
160. 相交链表 题目 给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。 图示两个链表在节点 c1 开始相交 ： 题目数据 保证 整个链式结构中不存在环。 注意 ，函数返回结果后，链表必须 保持其原始结构 。 自定义评测： 评测系统 的输入如下（你设计的程序 不适用 此输入）： intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0 listA - 第一个链表 listB - 第二个链表 skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数 skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数 评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。 示例 1： 输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2,...

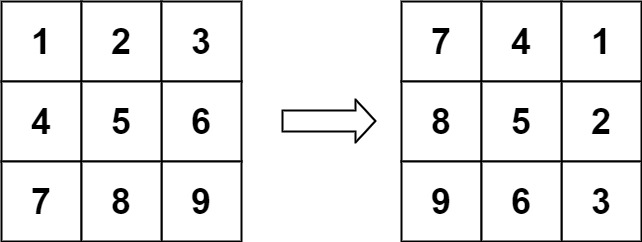
48. 旋转图像 题目 给定一个 \(n × n\) 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。 请不要 使用另一个矩阵来旋转图像。 示例 1： 输入：matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出：[[7,4,1],[8,5,2],[9,6,3]] 示例 2： 输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]] 提示： n == matrix.length == matrix[i].length 1 <= n <= 20 -1000 <= matrix[i][j] <= 1000 题解 这是一个经典的矩阵操作问题。要在原地（In-place）将图像顺时针旋转 90 度，我们可以利用矩阵的几何性质。 最直观且易于实现的方法是将...

SigLIP 概述 CLIP自提出以来在zero-shot分类、跨模态搜索、多模态对齐等多个领域得到广泛应用。得益于其令人惊叹的能力，激起了研究者广泛的关注和优化。 目前对CLIP的优化主要可以分为两大类： 其一是如何降低CLIP的训练成本； 其二是如何提升CLIP的performance。 对于第一类优化任务的常见思路有3种。 优化训练架构，如 LiT 通过freezen image encoder，单独训练text encoder来进行text 和image的对齐来加速训练； 减少训练token，如 FLIP 通过引入视觉mask，通过只计算非mask区域的视觉表征来实现加速（MAE中的思路） 优化目标函数，如 CatLIP 将caption转为class label，用分类任务来代替对比学习任务来实现加速。 对于第二类提升CLIP的performance最常用和有效的手段就是数据治理，即构建高质量、大规模、高多样性的图文数据，典型的工作如：DFN。 SigLIP这篇paper 提出用sigmoid...

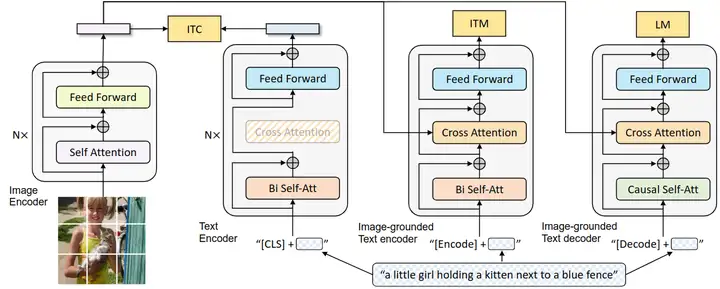
BLIP 论文名称 ：BLIP: Bootstrapping Language-Image Pre-training for Unified Vision-Language Understanding and Generation (ICML 2022) 论文地址： https://arxiv.org/pdf/2201.12086.pdf 代码地址： https://github.com/salesforce/BLIP 官方解读博客： https://blog.salesforceairesearch.com/blip-bootstrapping-language-image-pretraining/ 背景和动机 视觉语言训练 (Vision-Language Pre-training, VLP) 最近在各种多模态下游任务上取得了巨大的成功。然而，现有方法有两个主要限制： 模型层面： 大多数现有的预训练模型仅在基于理解的任务或者基于生成的任务方面表现出色，很少有可以兼顾的模型。比如，基于编码器的模型，像 CLIP，ALBEF 不能直接转移到文本生成任务...

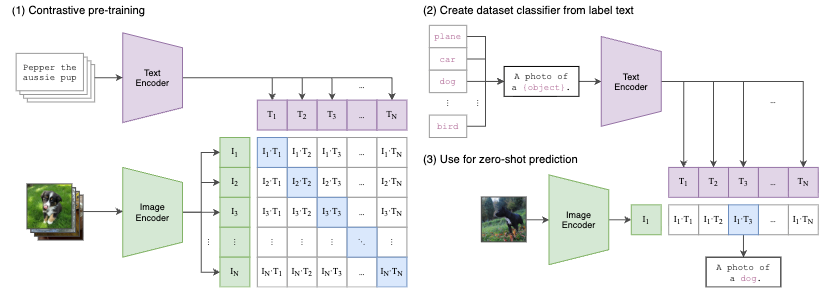
CLIP算法原理 CLIP 不预先定义图像和文本标签类别，直接利用从互联网爬取的 400 million 个image-text pair 进行图文匹配任务的训练，并将其成功迁移应用于30个现存的计算机视觉分类。简单的说，CLIP 无需利用 ImageNet 的数据和标签进行训练，就可以达到 ResNet50 在 ImageNet数据集上有监督训练的结果，所以叫做 Zero-shot。 CLIP（contrastive language-image pre-training）主要的贡献就是 利用无监督的文本信息，作为监督信号来学习视觉特征 。 CLIP 作者先是回顾了并总结了和上述相关的两条表征学习路线： 构建image和text的联系，比如利用已有的image-text pair数据集，从text中学习image的表征； 获取更多的数据（不要求高质量，也不要求full...

数组&链表&字符串 双指针 滑动窗口 哈希表 哈希表 栈&队列 单调队列 树与堆 图 数学 Math

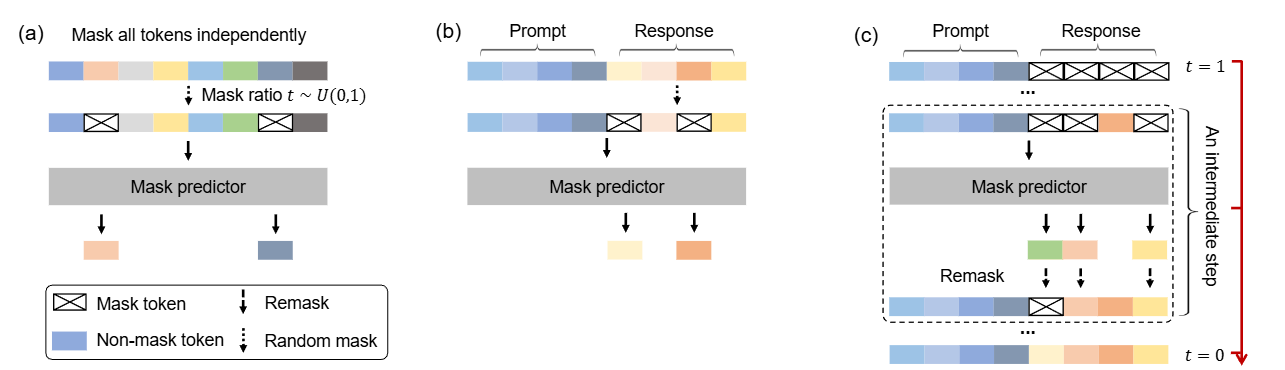
这是一篇尝试改变LLM「范式」的文章：当前主流的LLM架构都是「自回归」的，通俗地理解就是必须「从左到右依次生成」。这篇文章挑战了这一范式，探索扩散模型在 LLMs 上的可行性，通过 随机掩码 - 预测 的逆向思维，让模型学会「全局思考」。 论文： [2502.09992] Large Language Diffusion Models 背景 主流大语言模型架构：自回归模型 (Autoregressive LLMs) 过去几年， 自回归模型（Autoregressive Models, ARMs）一直是大语言模型(LLM)的主流架构​。典型的自回归语言模型以Transformer解码器为基础，按照从左到右 的顺序依次预测下一个词元(token)。 形式化地，自回归模型将一个长度为 \(N\) 的文本序列 \(X=(x_1, x_2, ..., x_N)\) 的概率分解为各位置的条件概率连乘积​： \[P_{\theta}(x_1, x_2, \dots, x_N) = \prod_{i=1}^{N} P_{\theta}(x_i \mid x_1, x_2, \dots,...

引言 Diffusion模型近年来在图像生成这一连续域任务中取得了显著成果，展现出强大的生成能力。然而，在文本生成这一离散域任务中整体效果仍不尽如人意，未能在该领域引起广泛关注。 去年，一篇研究离散扩散模型在文本生成的文章《Discrete Diffusion Modeling by Estimating the Ratios of the Data Distribution》获得ICML 2024的Best Paper，引发了学术界的广泛兴趣，也激发了新一轮的研究热潮。随后在2025年，越来越多高校和企业也开始积极探索基于Diffusion的文本生成方法。其中，近期备受关注的Block Diffusion也成功入选ICLR oral，进一步推动了该方向的发展。...

💡 扩散模型：通过加噪的方式去学习原始数据的分布， 从学到的分布中去生成样本 DDPM 关键点： 1. 正向加噪是离散时间马尔可夫链：从 \(x_0\) 逐步加噪得到 \(x_1,x_2,...,x_T\) ；在合适的噪声调度与足够大的 \(T\) 下， \(x_T\) 近似服从 \( N(0,I) \) 的各向同性高斯。 2. 每一步噪声方差 \(β_t\) 满足 \(0<β_t<1\) ，通常随 \(t\) 增大；因此 \(q(x_t|x_{t-1}) \) 的均值缩放系数 \(\sqrt{1-β_t} \) 逐渐减小。 3. 训练通过最大化对数似然的变分下界（ELBO）来学习反向过程 \( p_θ(x_{t-1}|x_t)\) ，并将其参数化为高斯分布（神经网络预测均值/噪声或 score）。 4. 将目标写成 score/DSM 形式时，loss 的权重与对应噪声层的方差尺度（如 \(1-\bar{α}_t\) 或相关量）有关；采样通常是按学习到的反向转移逐步生成（祖先采样），与经典 Langevin MCMC 更新形式不同，但可在 SDE 视角下统一理解。...

基于文章 《Elucidating the Design Space of Diffusion-Based Generative Models》 来统一扩散模型框架 通用扩散模型框架推导 加噪公式 Flow Matching的一步加噪公式 \[\mathbf{x}_t=(1-t)\mathbf{x}_0+t\varepsilon\] 写成概率分布形式： \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;(1-t)\mathbf{x}_0,t^2\mathbf{I})\] Score Matching的一步加噪公式 \[\mathbf{x}_t=\mathbf{x}_0+\sigma_t\varepsilon \] 写成概率分布形式： \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;\mathbf{x}_0,\sigma_t^2\mathbf{I})\] DDPM/DDIM的一步加噪公式...

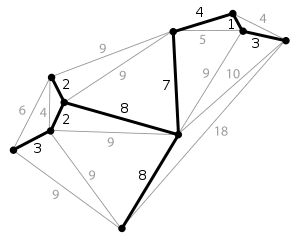
简介 生成树（spanning tree） 在图论中，无向图 G=(V,E) 的生成树（spanning tree)是具有G的全部顶点，但边数最少的联通子图。假设G中一共有n个顶点，一颗生成树满足下列条件： （1）n个顶点； （2）n1条边； （3）n个顶点联通； （4）一个图的生成树可能有多个。最小生成树（minimum spanning tree， MST）/最小生成森林：联通加权无向图中边缘权重加和最小的生成树。给定无向图 G=(V,E) ， (u,v) 代表顶点 u 与顶点 v 的边， w(u,v) 代表此边的权重，若存在生成树T使得： [公式] 最小，则 T 为 G 的最小生成树。对于非连通无向图来说，它的每一连通分量同样有最小生成树，它们的并被称为最小生成森林。最小生成树除了继承...

给一个无向图，判断其是否为一棵树。如果是树的话，所有的节点必须是连接的，也就是说必须是连通图，而且不能有环，所以就变成了验证是否是连通图和是否含有环。 [代码]