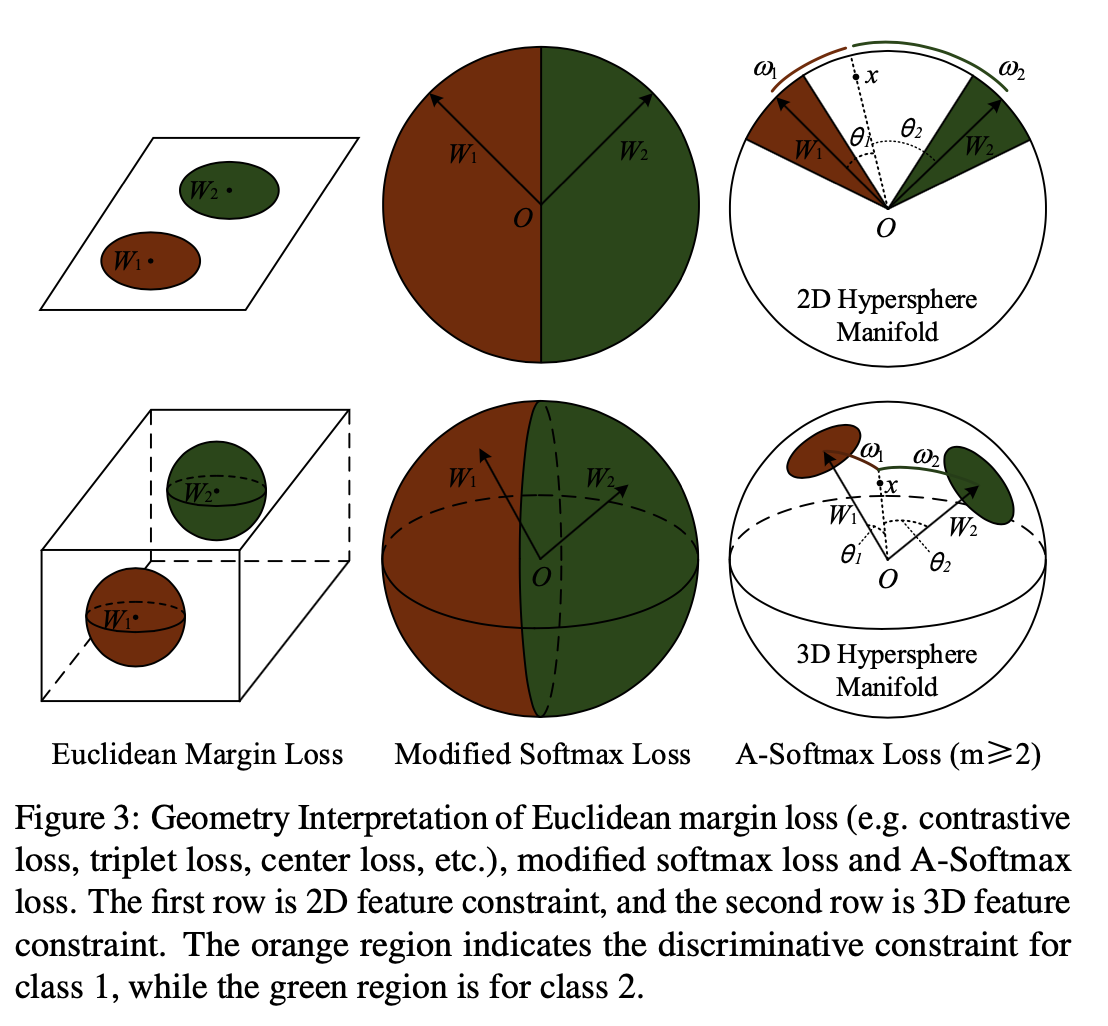
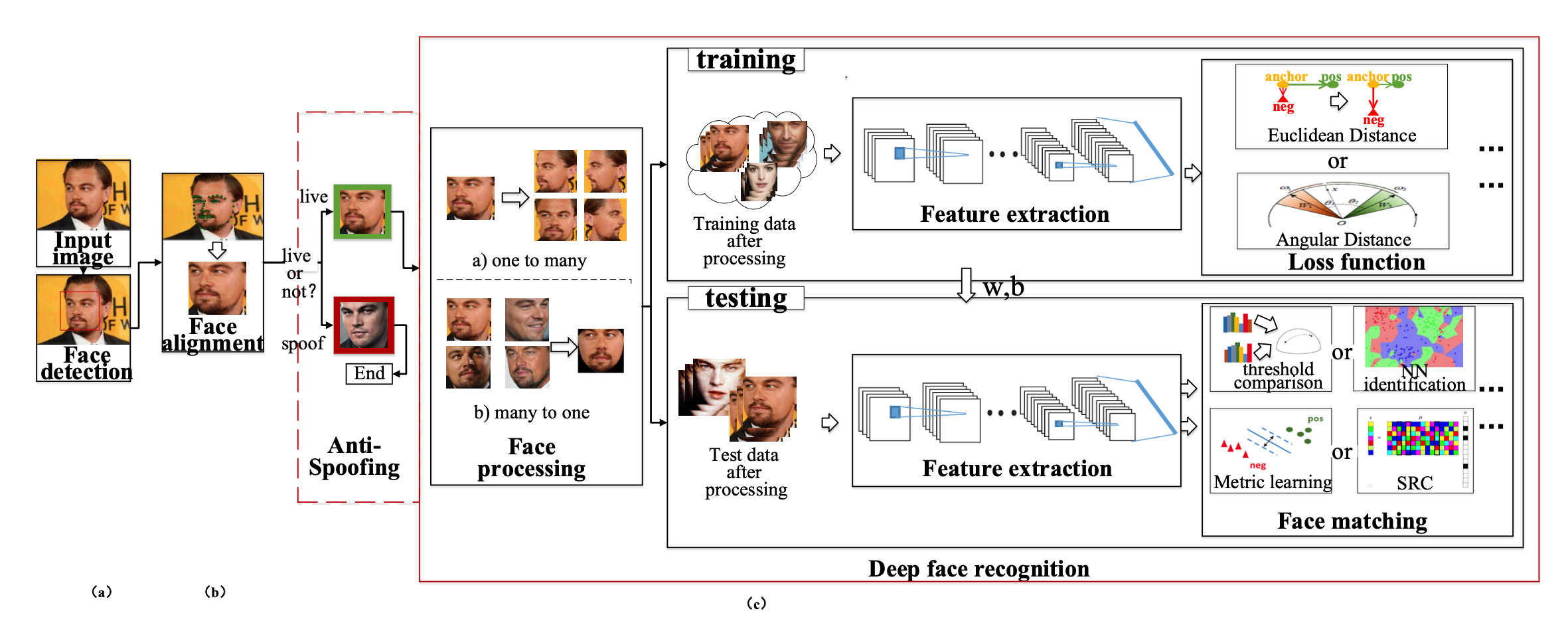
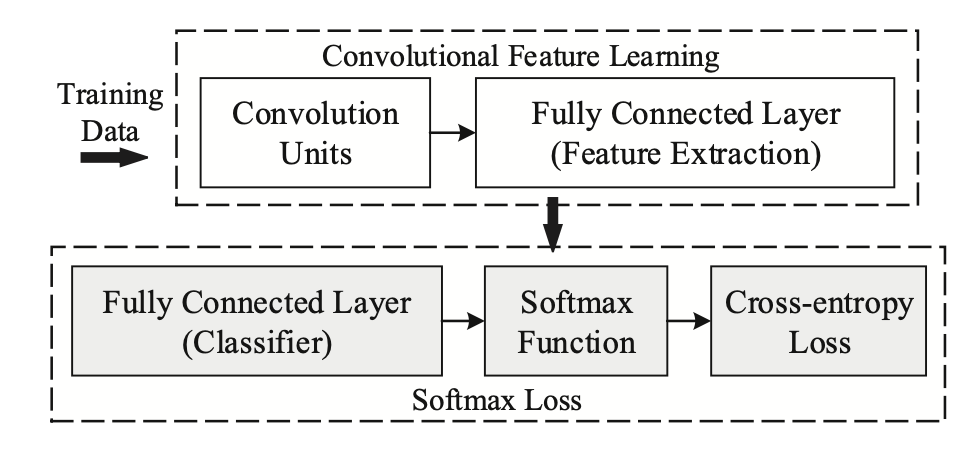
3D Model
2026-02-01
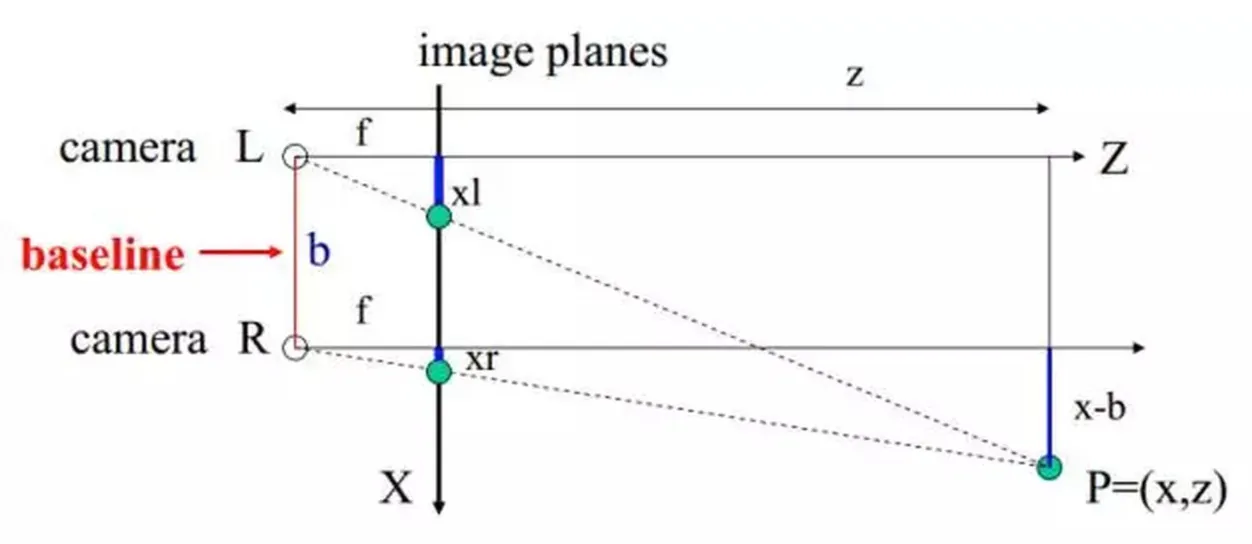
深度相机 “工欲善其事必先利其器‘’我们先从能够获取RGBD数据的相机开始谈起。首先我们来看一看其分类。 根据其工作原理主要分为三类: 1.双目方案 基于双目立体视觉的深度相机类似人类的双眼,和基于TOF、结构光原理的深度相机不同,它不对外主动投射光源,完全依靠拍摄的两张图片(彩色RGB或者灰度图)来计算深度,因此有时候也被称为被动双目深度相机。比较知名的产品有STEROLABS 推出的 ZED 2K Stereo Camera和Point Grey 公司推出的 BumbleBee。 双目立体视觉是基于视差原理,由多幅图像获取物体三维几何信息的方法。在机器视觉系统中, 双目视觉一般由双摄像机从不同角度同时获取周围景物的两幅数字图像,或有由单摄像机在不同时刻从不同角度获取周围景物的两幅数字图像 ,并基于视差原理即可恢复出物体三维几何信息,重建周围景物的三维形状与位置。 双目视觉有的时候我们也会把它称为体视,是人类利用双眼获取环境三维信息的主要途径。从目前来看,随着机器视觉理论的发展,双目立体视觉在机器视觉研究中发回来看了越来越重要的作用 为什么非得用双目相机才能得到深度?...