INCOMING TRANSMISSION

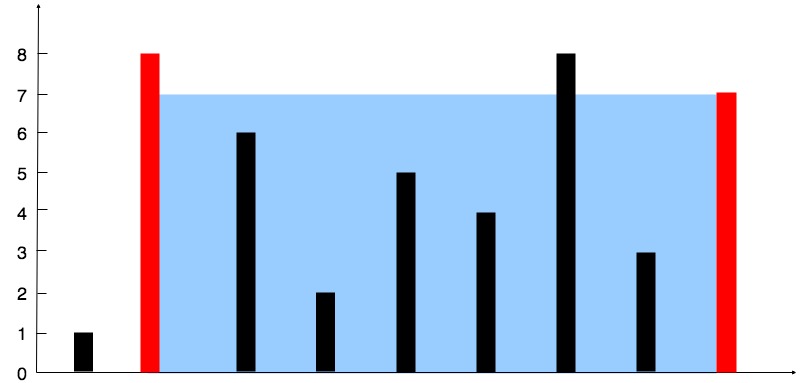
11. 盛最多水的容器 题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明： 你不能倾斜容器。 示例 1： 输入：[1,8,6,2,5,4,8,3,7] 输出：49 解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。 示例 2： 输入：height = [1,1] 输出：1 提示： n == height.length 2 <= n <= 10 5 0 <= height[i] <= 10 4 题解 在初始时，左右指针分别指向数组的左右两端，它们可以容纳的水量为 \(min(1,7)∗8=8\) 。 此时我们需要移动一个指针。移动哪一个呢？直觉告诉我们，应该移动对应数字较小的那个指针（即此时的左指针）。这是因为，由于容纳的水量是由 两个指针指向的数字中较小值∗指针之间的距离...

SigLIP 概述 CLIP自提出以来在zero-shot分类、跨模态搜索、多模态对齐等多个领域得到广泛应用。得益于其令人惊叹的能力，激起了研究者广泛的关注和优化。 目前对CLIP的优化主要可以分为两大类： 其一是如何降低CLIP的训练成本； 其二是如何提升CLIP的performance。 对于第一类优化任务的常见思路有3种。 优化训练架构，如 LiT 通过freezen image encoder，单独训练text encoder来进行text 和image的对齐来加速训练； 减少训练token，如 FLIP 通过引入视觉mask，通过只计算非mask区域的视觉表征来实现加速（MAE中的思路） 优化目标函数，如 CatLIP 将caption转为class label，用分类任务来代替对比学习任务来实现加速。 对于第二类提升CLIP的performance最常用和有效的手段就是数据治理，即构建高质量、大规模、高多样性的图文数据，典型的工作如：DFN。 SigLIP这篇paper 提出用sigmoid...

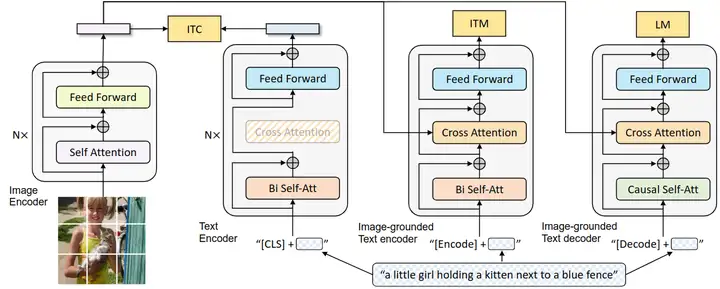
BLIP 论文名称 ：BLIP: Bootstrapping Language-Image Pre-training for Unified Vision-Language Understanding and Generation (ICML 2022) 论文地址： https://arxiv.org/pdf/2201.12086.pdf 代码地址： https://github.com/salesforce/BLIP 官方解读博客： https://blog.salesforceairesearch.com/blip-bootstrapping-language-image-pretraining/ 背景和动机 视觉语言训练 (Vision-Language Pre-training, VLP) 最近在各种多模态下游任务上取得了巨大的成功。然而，现有方法有两个主要限制： 模型层面： 大多数现有的预训练模型仅在基于理解的任务或者基于生成的任务方面表现出色，很少有可以兼顾的模型。比如，基于编码器的模型，像 CLIP，ALBEF 不能直接转移到文本生成任务...

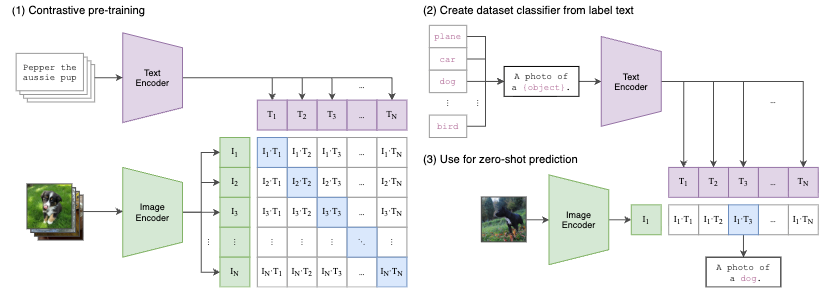
CLIP算法原理 CLIP 不预先定义图像和文本标签类别，直接利用从互联网爬取的 400 million 个image-text pair 进行图文匹配任务的训练，并将其成功迁移应用于30个现存的计算机视觉分类。简单的说，CLIP 无需利用 ImageNet 的数据和标签进行训练，就可以达到 ResNet50 在 ImageNet数据集上有监督训练的结果，所以叫做 Zero-shot。 CLIP（contrastive language-image pre-training）主要的贡献就是 利用无监督的文本信息，作为监督信号来学习视觉特征 。 CLIP 作者先是回顾了并总结了和上述相关的两条表征学习路线： 构建image和text的联系，比如利用已有的image-text pair数据集，从text中学习image的表征； 获取更多的数据（不要求高质量，也不要求full...

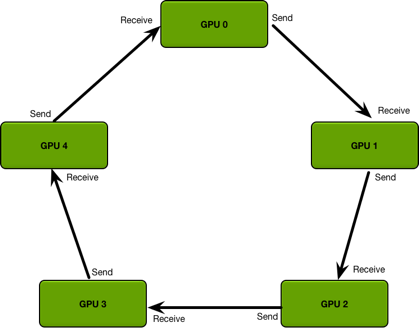
Quick Start 一个最简单的DDP Pytorch例子！ 环境准备 PyTorch(gpu)=1.5，python=3.6 推荐使用官方打好的PyTorch docker，避免乱七八糟的环境问题影响心情。 [代码] 代码 单GPU代码 [代码] 加入DDP的代码 [代码] DDP的基本原理 大白话原理 假如我们有N张显卡， 1. （缓解GIL限制）在DDP模式下，会有N个进程被启动，每个进程在一张卡上加载一个模型，这些模型的参数在数值上是相同的。 1. （RingReduce加速）在模型训练时，各个进程通过一种叫RingReduce的方法与其他进程通讯，交换各自的梯度，从而获得所有进程的梯度； 1. （实际上就是Data Parallelism）各个进程用平均后的梯度更新自己的参数，...

@tf_export为函数取了个名字！ Tensorflow经常看到定义的函数前面加了@tf_export。例如，tensorflow/python/platform/app.py中有： [代码] 首先，@tf_export是一个修饰符。修饰符的本质是一个函数 tf_export的实现在tensorflow/python/util/tf_export.py中： [代码] 等号的右边的理解分两步： 1. functools.partial 1. api_export functools.partial是偏函数,它的本质简而言之是为函数固定某些参数。如：functools.partial(FuncA, p1)的作用是把函数FuncA的第一个参数固定为p1；又如functools.partial(...

问题表示 有很多概率问题，尤其是独立重复实验问题，如果用生成函数的方法来做，会显得特别方便。本文要讲的“随机游走”问题便是其中一例，它又被形象地叫做“醉汉问题”，其本质上是一个二项分布，但是由于取了极限，出现了很多新的性质和应用。我们先考虑如下问题： 考虑实数轴上的一个粒子，在 t=0 时刻它位于原点，每过一秒，它要不向前移动一格（+1），要不就向后移动一格（1），问 n 秒后它所处位置的概率分布。 不难发现，这个问题跟二项分布是雷同的。如果把这个粒子形象比喻成一个“喝醉酒的人”，那么上面的走法就类似于一个完全不省人事的醉汉走路问题了。（当然，醉汉是在三维空间走路的，这里简单起见，只描述了一维...

PyTorch中，所有神经网络的核心是 autograd 包。 autograd 包为张量上的所有操作提供了自动求导机制。它是一个在运行时定义(definebyrun）的框架，这意味着反向传播是根据代码如何运行来决定的，并且每次迭代可以是不同的. 让我们用一些简单的例子来看看吧。 张量 torch.Tensor 是这个包的核心类。如果设置它的属性 .requires_grad 为 True，那么它将会追踪对于该张量的所有操作。当完成计算后可以通过调用 .backward()，来自动计算所有的梯度。这个张量的所有梯度将会自动累加到.grad属性. 要阻止一个张量被跟踪历史，可以调用 .detach() 方法将其与计算历史分离，并阻止它未来的计算记录被跟踪。 为了防止跟踪历史记录(和使用内存），...

相同点 nn.Xxx和nn.functional.xxx的实际功能是相同的，即nn.Conv2d和nn.functional.conv2d 都是进行卷积，nn.Dropout 和nn.functional.dropout都是进行dropout，。。。。。； 运行效率也是近乎相同。 nn.functional.xxx是函数接口，而nn.Xxx是nn.functional.xxx的类封装，并且nn.Xxx都继承于一个共同祖先nn.Module。这一点导致nn.Xxx除了具有nn.functional.xxx功能之外，内部附带了nn.Module相关的属性和方法，例如train(), eval(),load_state_dict, state_dict 等。 不同点 两者的调用方式不同。 nn.X...

问题定义 多元二次多项式，维度为 n ，那么可以用以下公式描述该函数： [Formula] 其中 a_{i,j} 为二次项系数，共有 n^2 项， 1≤i,j≤n ，且所有的 a 不全为0，即 ∃a_{i,j}≠0 ; b_k 为一次项系数，共 n 项， 1≤k≤n ; c 为常数项。 记 f(x)=[x_1,x_2,...,x_n]^T ，则上述函数可以写作二次型的形式： 转化过程中A,b满足： A 为n阶对称方阵， A_{i,j}=a_{i,j} 因为 ∃a_{i,j}≠0 ，A不为零矩阵 b_i=b_i 为了后续计算简便，我们将二次型稍作改动： [Formula] 我们的目标就是寻找该函...

基本概念 方向导数：是一个数；反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 偏导数：是多个数（每元有一个）；是指多元函数沿坐标轴方向的方向导数，因此二元函数就有两个偏导数。 偏导函数：是一个函数；是一个关于点的偏导数的函数。 梯度：是一个向量；每个元素为函数对一元变量的偏导数；它既有大小（其大小为最大方向导数），也有方向。 方向导数 反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 例子如下： 题目 设二元函数 f(x, y) = x^2 + y^2 ，分别计算此函数在点 (1, 2) 沿方向 w=\{3, 4\} 与方向 u=\{1, 0\} 的方向导数。 解： ...

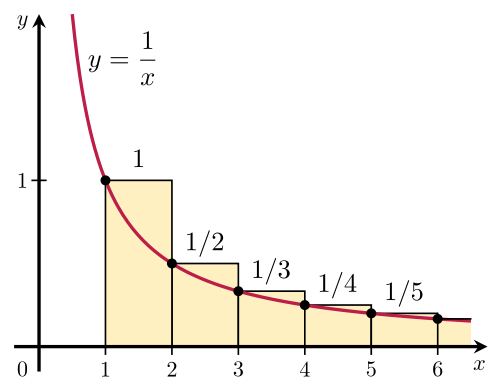
调和级数记住下面的公式就够了： [Formula] 证明方法就是下面这张图