INCOMING TRANSMISSION

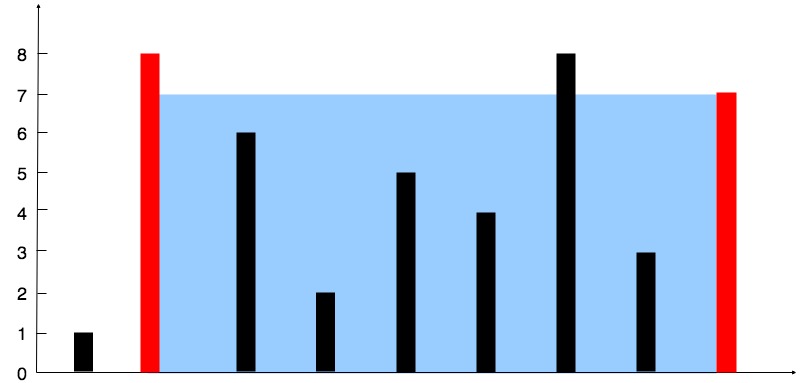
11. 盛最多水的容器 题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明： 你不能倾斜容器。 示例 1： 输入：[1,8,6,2,5,4,8,3,7] 输出：49 解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。 示例 2： 输入：height = [1,1] 输出：1 提示： n == height.length 2 <= n <= 10 5 0 <= height[i] <= 10 4 题解 在初始时，左右指针分别指向数组的左右两端，它们可以容纳的水量为 \(min(1,7)∗8=8\) 。 此时我们需要移动一个指针。移动哪一个呢？直觉告诉我们，应该移动对应数字较小的那个指针（即此时的左指针）。这是因为，由于容纳的水量是由 两个指针指向的数字中较小值∗指针之间的距离...

文章从连续情形出发开始介绍重参数，主要的例子是正态分布的重参数；然后引入离散分布的重参数，这就涉及到了Gumbel Softmax，包括Gumbel Softmax的一些证明和讨论；最后再讲讲重参数背后的一些故事，这主要跟梯度估计有关。 基本概念 重参数（Reparameterization） 实际上是处理如下期望形式的目标函数的一种技巧： \[L_{\theta}=\mathbb{E}_{z\sim p_{\theta}(z)}[f(z)]\tag{1}\] 这样的目标在VAE中会出现，在文本GAN也会出现，在强化学习中也会出现（ \(f(z)\) 对应于奖励函数），所以深究下去，我们会经常碰到这样的目标函数。取决于 \(z\) 的连续性，它对应不同的形式： \[\int p_{\theta}(z) f(z)dz\,\,\,\text{(连续情形)}\qquad\qquad \sum_{z} p_{\theta}(z) f(z)\,\,\,\text{(离散情形)}\tag{2}\] 当然，离散情况下我们更喜欢将记号 \(z\) 换成 \(y\) 或者 \(c\) 。 为了最小化...

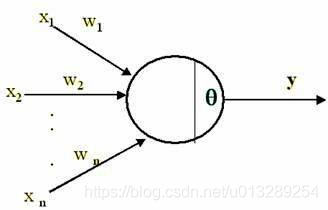
1.深度学习偏置的作用？ 我们在学深度学习的时候，最早接触到的神经网络应该属于感知器（感知器本身就是一个很简单的神经网络，也许有人认为它不属于神经网络，当然认为它和神经网络长得像也行） 要想激活这个感知器，使得 y=1 ，就必须使 x_1w_1 + x_2w_2 +....+x_nw_n T （ T 为一个阈值），而 T 越大，想激活这个感知器的难度越大，人工选择一个阈值并不是一个好的方法，因为样本那么多，我不可能手动选择一个阈值，使得模型整体表现最佳，那么我们可以使得T变成可学习的，这样一来， T 会自动学习到一个数，使得模型的整体表现最佳。当把T移动到左边，它就成了偏置， x_1w_1 + x_2w_2 +....+x_nw_n T 0 xw +b 0 ，总之，偏置的大小控制着激活这个感...

一般来说，神经网络处理的东西都是连续的浮点数，标准的输出也是连续型的数字。但实际问题中，我们很多时候都需要一个离散的结果，比如分类问题中我们希望输出正确的类别，“类别”是离散的，“类别的概率”才是连续的；又比如我们很多任务的评测指标实际上都是离散的，比如分类问题的正确率和F1、机器翻译中的BLEU，等等。 还是以分类问题为例，常见的评测指标是正确率，而常见的损失函数是交叉熵。交叉熵的降低与正确率的提升确实会有一定的关联，但它们不是绝对的单调相关关系。换句话说，交叉熵下降了，正确率不一定上升。显然，如果能用正确率的相反数做损失函数，那是最理想的，但正确率是不可导的（涉及到 [Math] 等操作），所以没法直接用。 这时候一般有两种解决方案；一是动用强化学习，将正确率设为奖励函数，这是“用牛刀杀...

如何计算RF 公式一：这个算法从top往下层层迭代直到追溯回input image，从而计算出RF。 [公式] 其中，RF是感受野。RF和RF有点像，N代表 neighbour，指的是第n层的 a feature在n1层的RF，记住N_RF只是一个中间变量，不要和RF混淆。 stride是步长，ksize是卷积核大小。

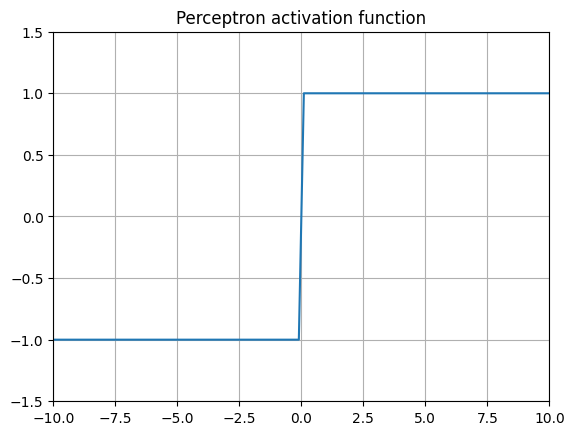
最近，似乎现在每个大型语言模型（LLM）和新闻中提到的复杂神经网络架构都使用略有不同的激活函数，而就在几年前，最常见的做法只是在神经网络的内部层中使用 ReLU。 曾经优秀的 ReLUs 怎么了，以及是什么促使最新的大型语言模型（LLMs）的创造者们开始使用不同的（更高级的）激活函数？ Threshold activation (Perceptron) 1957 年，罗森布拉特建造了“感知机” 最古老的激活函数是基本感知器。它由芝加哥大学精神病学系的爱德华·麦克洛奇和沃尔特·皮茨构思，后来由弗兰克·罗森布拉特在 1957 年于康奈尔航空实验室为美国海军在硬件上更著名地实现了。该算法非常简单，其基本规则是：如果某个值超过某个阈值，则返回 1，否则返回 0。有些变体会返回 1 或1。 由于其二元...

引言与背景 随机逼近（Stochastic Approximation）是一类用于求解寻根或优化问题的随机迭代算法，其特点是不需要知道目标函数或其导数的表达式。 随机逼近的核心优势在于： 能够处理带有随机噪声的观测数据 不需要目标函数的解析表达式 可以在线学习，每获得一个新样本就更新估计值 均值估计问题 考虑一个随机变量 X ，其取值来自有限集合 [Math] 。我们的目标是估计 E[X] 。假设我们有一个独立同分布的样本序列 \{x_i\}_{i=1}^n ，那么 X 的期望值可以近似为： [公式] 非增量方法与增量方法 非增量方法：先收集所有样本，然后计算平均值。缺点是如果样本数量很大，可能需要等待很长时间。 增量方法：定义 [公式] 可以推导出递归公式： [公式] 这个算法可以增量式地...

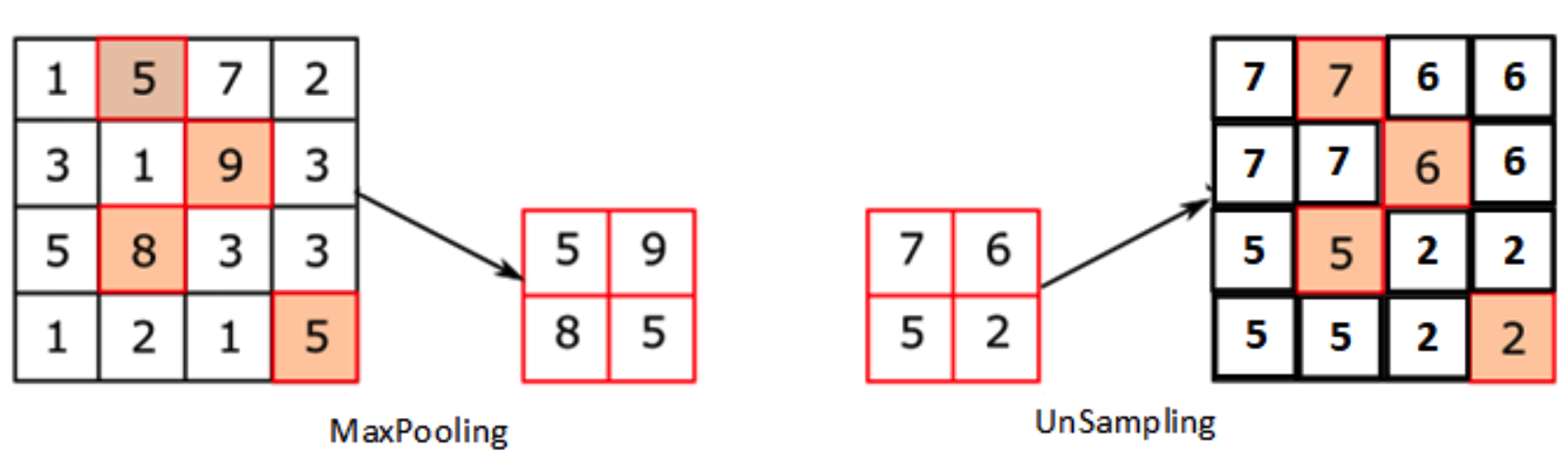
通过卷积和池化等技术可以将图像进行降维，因此，一些研究人员也想办法恢复原分辨率大小的图像，特别是在语义分割领域应用很成熟。 1、Upsampling（上采样）[没有学习过程] 在FCN、Unet等网络结构中，涉及到了上采样。上采样概念：上采样指的是任何可以让图像变成更高分辨率的技术。最简单的方式是重采样和插值：将输入图片进行rescale到一个想要的尺寸，而且计算每个点的像素点，使用如双线性插值等插值方法对其余点进行插值来完成上采样过程。 在PyTorch中，上采样的层被封装在torch.nn中的Vision Layers里面，一共有4种： PixelShuffle Upsample UpsamplingNearest2d UpsamplingBilinear2d 0）PixelShuffl...

摘掉Softmax 制约Attention性能的关键因素，其实是定义里边的Softmax！事实上，简单地推导一下就可以得到这个结论。 [Math] 这一步我们得到一个 [Math] 的矩阵，就是这一步决定了Attention的复杂度是 [Math] ；如果没有Softmax，那么就是三个矩阵连乘 [Math] ，而矩阵乘法是满足结合率的，所以我们可以先算 [Math] ，得到一个 [Math] 的矩阵，然后再用 [Math] 左乘它，由于 [Math] ，所以这样算大致的复杂度只是 [Math] （就是 [Math] 左乘那一步占主导）。 也就是说，去掉Softmax的Attention的复杂度可以降到最理想的线性级别 [Math] ！这显然就是我们的终极追求：Linear Attentio...

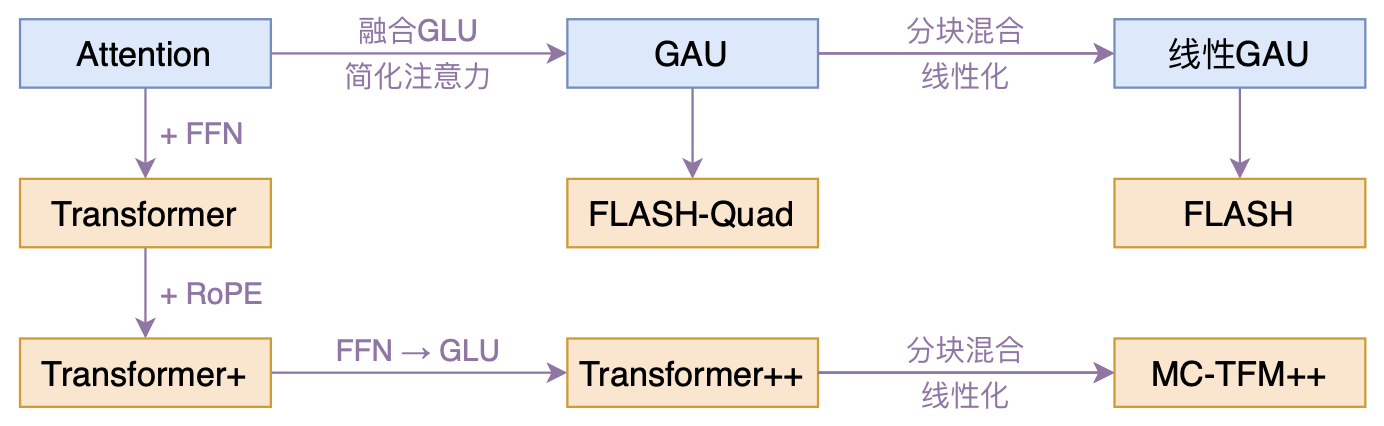
概述 本文介绍一个比较有意思的高效Transformer工作——来自Google的《Transformer Quality in Linear Time》，经过细读之后，笔者认为论文里边真算得上是“惊喜满满”了～ 什么样的结果值得我们用“惊喜”来形容？有没有言过其实？我们不妨先来看看论文做到了什么： 1. 提出了一种新的Transformer变体，它依然具有二次的复杂度，但是相比标准的Transformer，它有着更快的速度、更低的显存占用以及更好的效果； 1. 提出一种新的线性化Transformer方案，它不但提升了原有线性Attention的效果，还保持了做Decoder的可能性，并且做Decoder时还能保持高效的训练并行性。 说实话，笔者觉得做到以上任意一点都是非常难得的，而这篇论...

AdamW目前是大语言模型训练的默认优化器，而大部分资料对Adam跟AdamW区别的介绍都不是很明确，在此梳理一下Adam与AdamW的计算流程，明确一下二者的区别。 TLDR：AdamW将优化过程中使用的针对网络权重的衰减项（或者叫正则项）从loss中单独拿了出来，不参与Adam中一二阶动量的计算。 下面是二者的详细对比： Adam 首先是Adam，给定在迭代步数 t 时模型的参数 [Math] 与梯度 g_t ，Adam的计算公式如下： [公式] 式(1)用于计算梯度的一阶指数滑动平均 式(2)用于计算梯度的二阶项的指数滑动平均 式(3)与(4)对计算得到的指数滑动平均值进行消偏 式(5)为Adam的更新公式，其可以拆成两部分理解：动量更新与自适应学习率。 AdamW AdamW 相对与...

概述 SSM的概念由来已久，但这里我们特指深度学习中的SSM，一般认为其开篇之作是2021年的 S4，不算太老，而SSM最新最火的变体大概是Mamba。当然，当我们谈到SSM时，也可能泛指一切线性RNN模型，这样RWKV、RetNet还有此前LRU都可以归入此类。不少SSM变体致力于成为Transformer的竞争者，尽管笔者并不认为有完全替代的可能性，但SSM本身优雅的数学性质也值得学习一番。 尽管我们说SSM起源于S4，但在S4之前，SSM有一篇非常强大的奠基之作《HiPPO: Recurrent Memory with Optimal Polynomial Projections》（简称HiPPO），所以本文从HiPPO开始说起。 另外值得一提的是，SSM代表作HiPPO、S4、Mam...