INCOMING TRANSMISSION

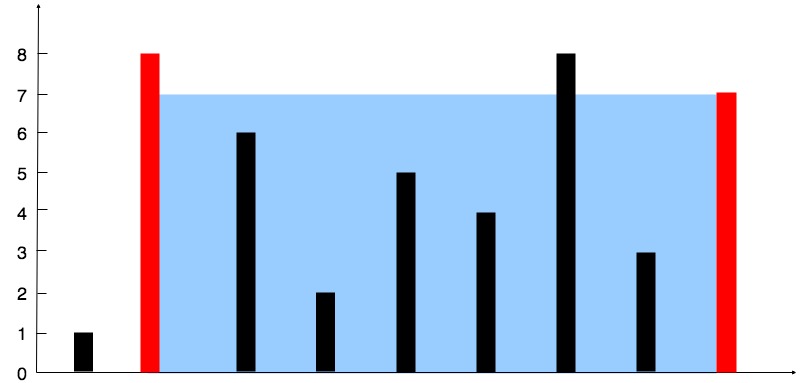
11. 盛最多水的容器 题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明： 你不能倾斜容器。 示例 1： 输入：[1,8,6,2,5,4,8,3,7] 输出：49 解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。 示例 2： 输入：height = [1,1] 输出：1 提示： n == height.length 2 <= n <= 10 5 0 <= height[i] <= 10 4 题解 在初始时，左右指针分别指向数组的左右两端，它们可以容纳的水量为 \(min(1,7)∗8=8\) 。 此时我们需要移动一个指针。移动哪一个呢？直觉告诉我们，应该移动对应数字较小的那个指针（即此时的左指针）。这是因为，由于容纳的水量是由 两个指针指向的数字中较小值∗指针之间的距离...

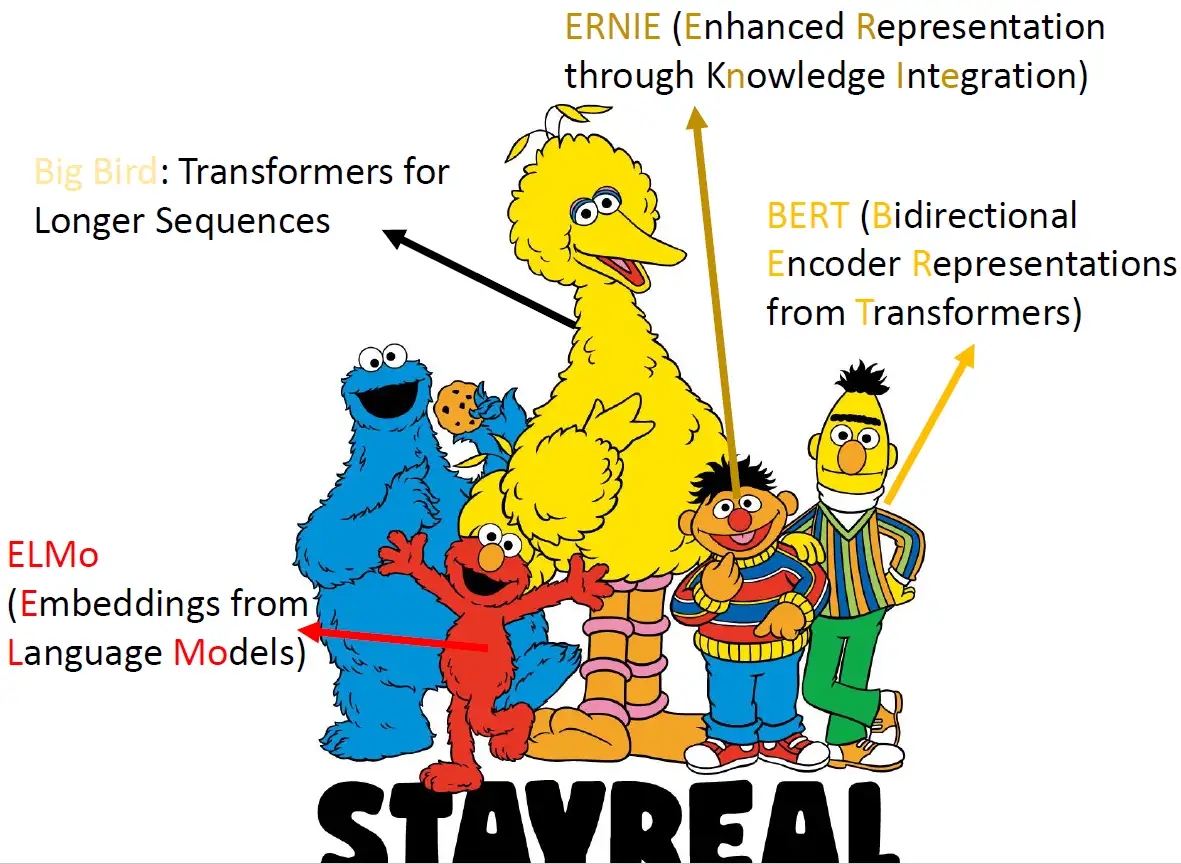
Self-Supervised Learning ，又称为自监督学习，我们知道一般机器学习分为有监督学习，无监督学习和强化学习。 而 Self-Supervised Learning 是无监督学习里面的一种，主要是希望能够学习到一种 通用的特征表达 用于 下游任务 (Downstream Tasks) 。 其主要的方式就是通过自己监督自己。作为代表作的 kaiming 的 MoCo 引发一波热议， Yann Lecun也在 AAAI 上讲 Self-Supervised Learning 是未来的大势所趋。所以在这个系列中，我会系统地解读 Self-Supervised Learning 的经典工作。 本文主要介绍 Self-Supervised Learning 在 NLP领域 的经典工作：BERT模型的原理及其变体。 本文来自台湾大学李宏毅老师PPT： https://speech.ee.ntu.edu.tw/~hylee/ml/ml2021-course-data/bert_v8.pdf 芝麻街 在介绍 Self-Supervised Learning...

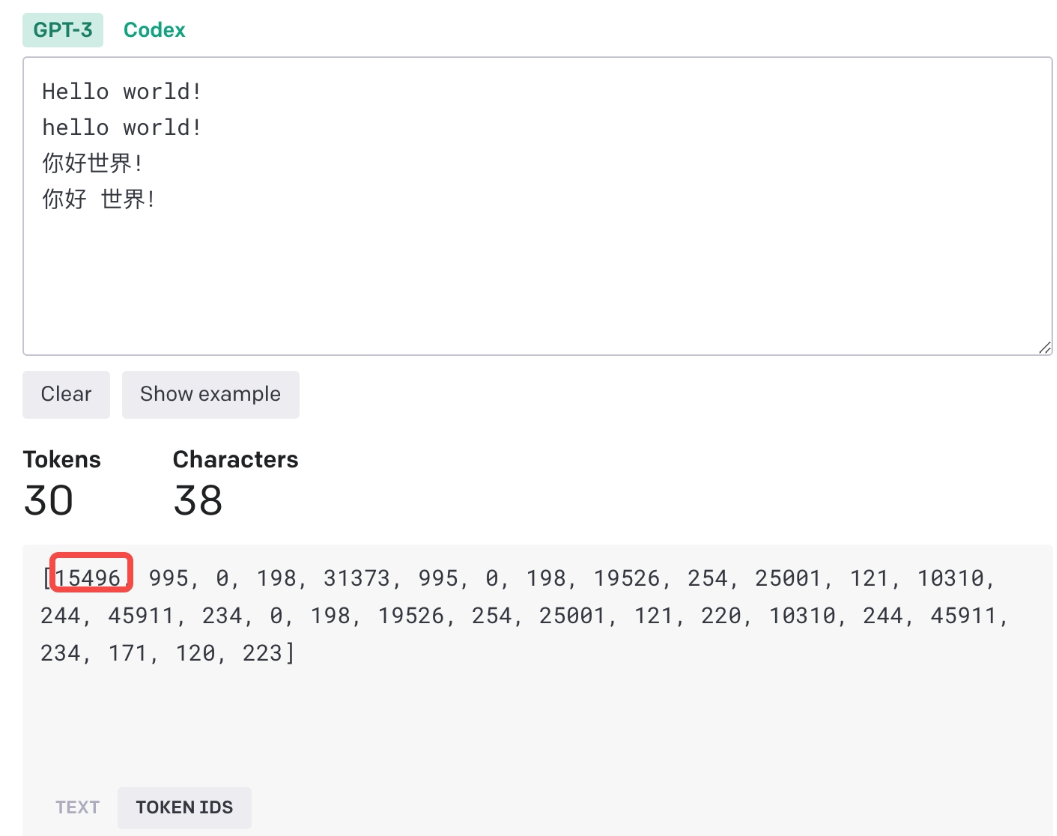
Tokenizer 诸如GPT3/4以及LlaMA/LlaMA2大语言模型都采用了token的作为模型的输入输出，其输入是文本，然后将文本转为token（正整数），然后从一串token（对应于文本）预测下一个token。 进入OpenAI官网提供的tokenizer可以看到GPT3tokenizer采用的方法。这里以Hello World为例说明。 总共30个token，英文单词一般会用单独的token表示，大小写也会区分不同的token，如Hello和hello，另外有一些由空格前导的单词也会单独编码，这会使得编码整个句子效率更高（这将省去每个空格的编码），对于中文token化，会使用两到三个ID（正整数表示），比如上面的中英文的！。 在英语等空白隔开的语言中，文本被预标记化，通常使用不跨...

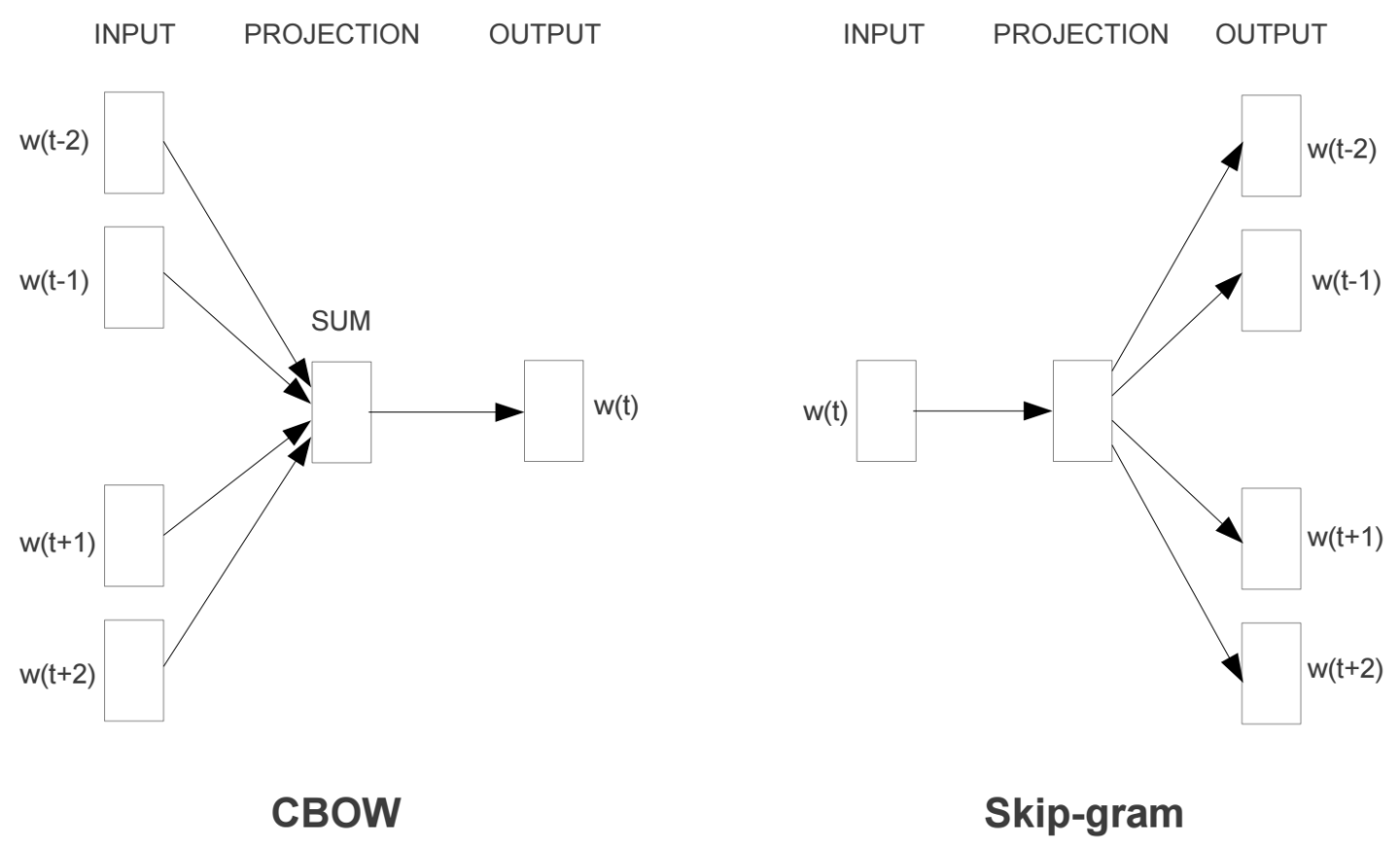
什么是Word2Vec和Embeddings？ Word2Vec是从大量文本语料中以无监督的方式学习语义知识的一种模型，它被大量地用在自然语言处理（NLP）中。那么它是如何帮助我们做自然语言处理呢？Word2Vec其实就是通过学习文本来用词向量的方式表征词的语义信息，即通过一个嵌入空间使得语义上相似的单词在该空间内距离很近。Embedding其实就是一个映射，将单词从原先所属的空间映射到新的多维空间中，也就是把原先词所在空间嵌入到一个新的空间中去。 我们从直观角度上来理解一下，cat这个单词和kitten属于语义上很相近的词，而dog和kitten则不是那么相近，iphone这个单词和kitten的语义就差的更远了。通过对词汇表中单词进行这种数值表示方式的学习（也就是将单词转换为词向量），能...

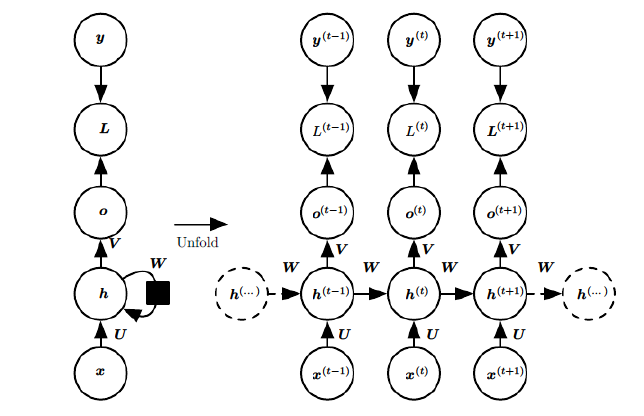
RNN 概述 在前面讲到的DNN和CNN中，训练样本的输入和输出是比较的确定的。但是有一类问题DNN和CNN不好解决，就是训练样本输入是连续的序列,且序列的长短不一，比如基于时间的序列：一段段连续的语音，一段段连续的手写文字。这些序列比较长，且长度不一，比较难直接的拆分成一个个独立的样本来通过DNN/CNN进行训练。 而对于这类问题，RNN则比较的擅长。那么RNN是怎么做到的呢？RNN假设我们的样本是基于序列的。比如是从序列索引1到序列索引 τ 。对于这其中的任意序列索引号 t ,它对应的输入是对应的样本序列中的 x(t) 。而模型在序列索引号 t 位置的隐藏状态 h(t) ，则由 x(t) 和在 t−1 位置的隐藏状态 h(t−1) 共同决定。在任意序列索引号 t ，我们也有对应的模型预测...

梯度检查点（Gradient Checkpointing） 大模型的参数量巨大，即使将batch_size设置为1并使用梯度累积的方式更新，也仍然会OOM。原因是通常在计算梯度时，我们需要将所有前向传播时的激活值保存下来，这消耗大量显存。 还有另外一种延迟计算的思路，丢掉前向传播时的激活值，在计算梯度时需要哪部分的激活值就重新计算哪部分的激活值，这样做倒是解决了显存不足的问题，但加大了计算量同时也拖慢了训练。 梯度检查点（Gradient Checkpointing）在上述两种方式之间取了一个平衡，这种方法采用了一种策略选择了计算图上的一部分激活值保存下来，其余部分丢弃，这样被丢弃的那一部分激活值需要在计算梯度时重新计算。 下面这个动图展示了一种简单策略：前向传播过程中计算节点的激活值并保存...

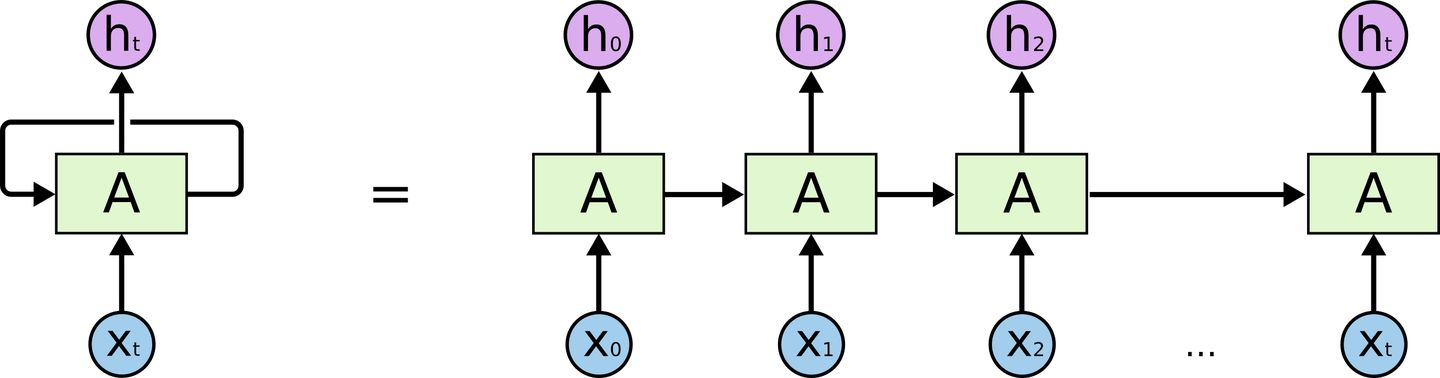
取代RNN——Transformer 在介绍Transformer前我们来回顾一下RNN的结构 对RNN有一定了解的话，一定会知道，RNN有两个很明显的问题 效率问题：需要逐个词进行处理，后一个词要等到前一个词的隐状态输出以后才能开始处理 如果传递距离过长还会有梯度消失、梯度爆炸和遗忘问题 为了缓解传递间的梯度和遗忘问题，设计了各种各样的RNN cell，最著名的两个就是LSTM和GRU了 LSTM (Long Short Term Memory) GRU (Gated Recurrent Unit) 但是，引用网上一个博主的比喻，这么做就像是在给马车换车轮，为什么不直接换成汽车呢？ 于是就有了Transformer。Transformer 是Google Brain 2017的提出的一篇工...

问题表示 有很多概率问题，尤其是独立重复实验问题，如果用生成函数的方法来做，会显得特别方便。本文要讲的“随机游走”问题便是其中一例，它又被形象地叫做“醉汉问题”，其本质上是一个二项分布，但是由于取了极限，出现了很多新的性质和应用。我们先考虑如下问题： 考虑实数轴上的一个粒子，在 t=0 时刻它位于原点，每过一秒，它要不向前移动一格（+1），要不就向后移动一格（1），问 n 秒后它所处位置的概率分布。 不难发现，这个问题跟二项分布是雷同的。如果把这个粒子形象比喻成一个“喝醉酒的人”，那么上面的走法就类似于一个完全不省人事的醉汉走路问题了。（当然，醉汉是在三维空间走路的，这里简单起见，只描述了一维...

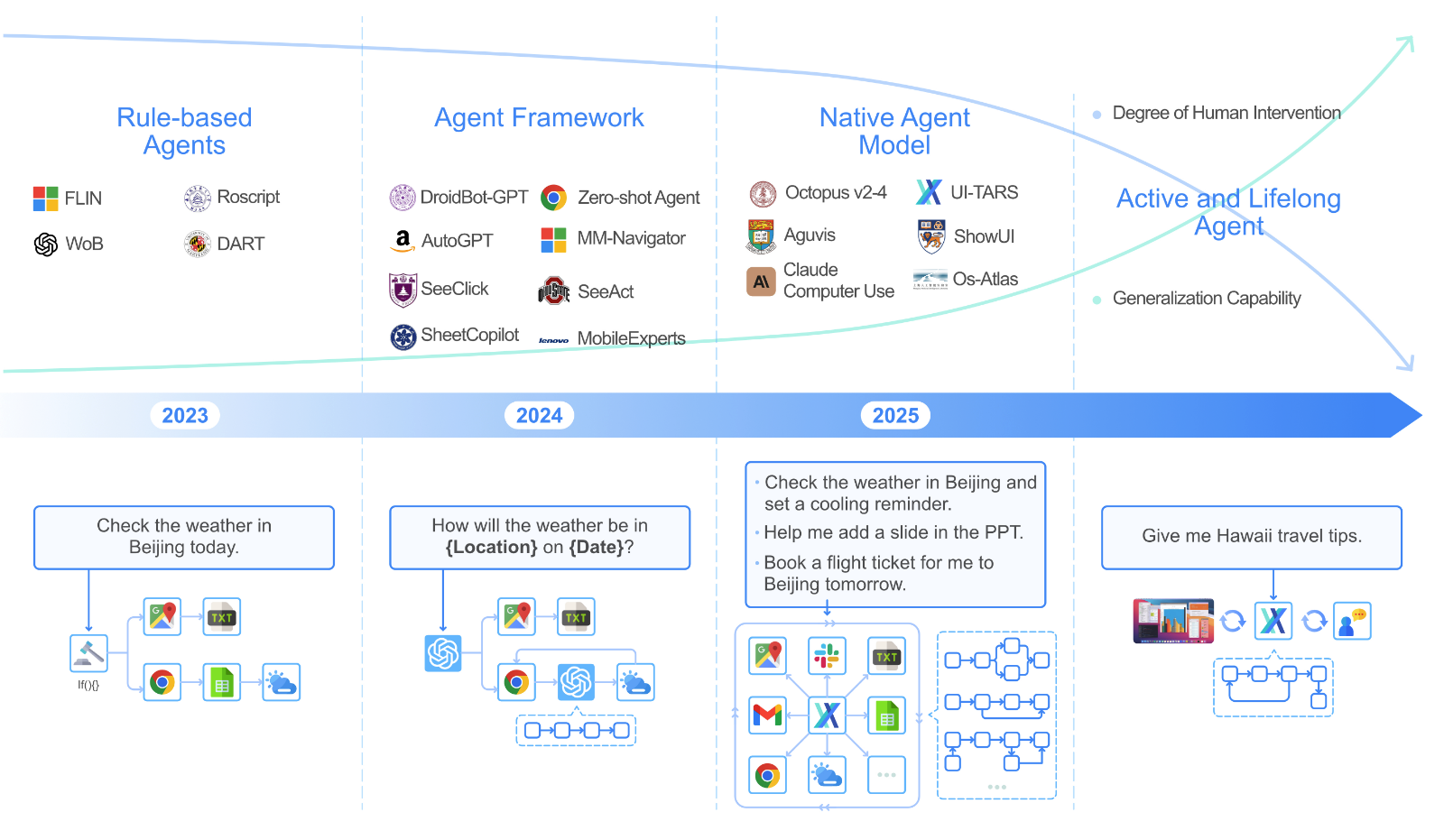
UITARS 简介 UITARS（User Interface Task Automation and Reasoning System）是由字节跳动（ByteDance）研发的原生 GUI 智能体模型： 输入方式：仅使用屏幕截图作为视觉输入 交互方式：执行类人操作（键盘输入、鼠标点击、拖拽等） 模型特性：端到端的原生智能体模型，无需复杂的中间件或框架 传统 GUI 智能体的开发往往依赖于文本信息，例如 HTML 结构和可访问性树。虽然这些方法取得了一些进展，但它们也存在一些局限性： 平台不一致性：不同平台的 GUI 结构差异很大，导致智能体难以跨平台通用。 信息冗余：文本信息往往过于冗长，增加了模型的处理负担。 访问限制：获取系统底层的文本信息通常需要较高的权限，限制了应用的范围。 模块化...

概述 SSM的概念由来已久，但这里我们特指深度学习中的SSM，一般认为其开篇之作是2021年的 S4，不算太老，而SSM最新最火的变体大概是Mamba。当然，当我们谈到SSM时，也可能泛指一切线性RNN模型，这样RWKV、RetNet还有此前LRU都可以归入此类。不少SSM变体致力于成为Transformer的竞争者，尽管笔者并不认为有完全替代的可能性，但SSM本身优雅的数学性质也值得学习一番。 尽管我们说SSM起源于S4，但在S4之前，SSM有一篇非常强大的奠基之作《HiPPO: Recurrent Memory with Optimal Polynomial Projections》（简称HiPPO），所以本文从HiPPO开始说起。 另外值得一提的是，SSM代表作HiPPO、S4、Mam...

问题定义 多元二次多项式，维度为 n ，那么可以用以下公式描述该函数： [Formula] 其中 a_{i,j} 为二次项系数，共有 n^2 项， 1≤i,j≤n ，且所有的 a 不全为0，即 ∃a_{i,j}≠0 ; b_k 为一次项系数，共 n 项， 1≤k≤n ; c 为常数项。 记 f(x)=[x_1,x_2,...,x_n]^T ，则上述函数可以写作二次型的形式： 转化过程中A,b满足： A 为n阶对称方阵， A_{i,j}=a_{i,j} 因为 ∃a_{i,j}≠0 ，A不为零矩阵 b_i=b_i 为了后续计算简便，我们将二次型稍作改动： [Formula] 我们的目标就是寻找该函...

基本概念 方向导数：是一个数；反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 偏导数：是多个数（每元有一个）；是指多元函数沿坐标轴方向的方向导数，因此二元函数就有两个偏导数。 偏导函数：是一个函数；是一个关于点的偏导数的函数。 梯度：是一个向量；每个元素为函数对一元变量的偏导数；它既有大小（其大小为最大方向导数），也有方向。 方向导数 反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 例子如下： 题目 设二元函数 f(x, y) = x^2 + y^2 ，分别计算此函数在点 (1, 2) 沿方向 w=\{3, 4\} 与方向 u=\{1, 0\} 的方向导数。 解： ...