INCOMING TRANSMISSION

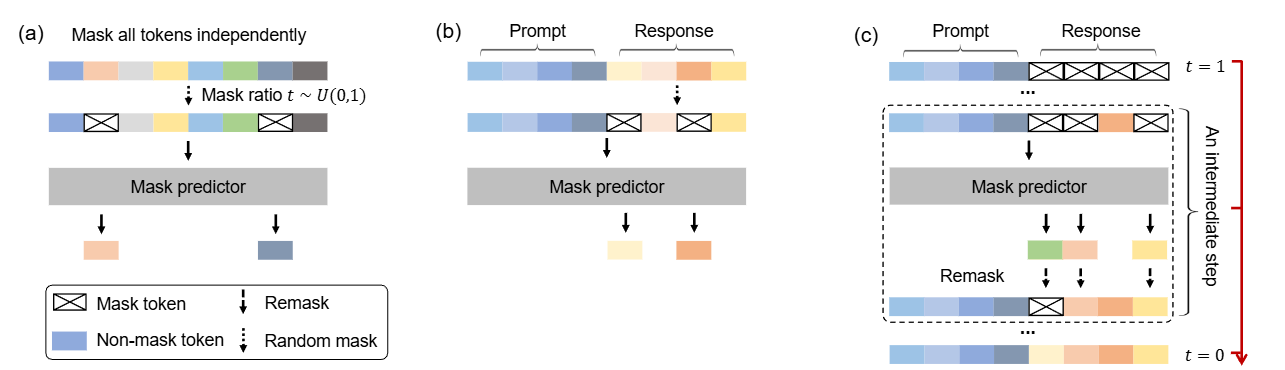
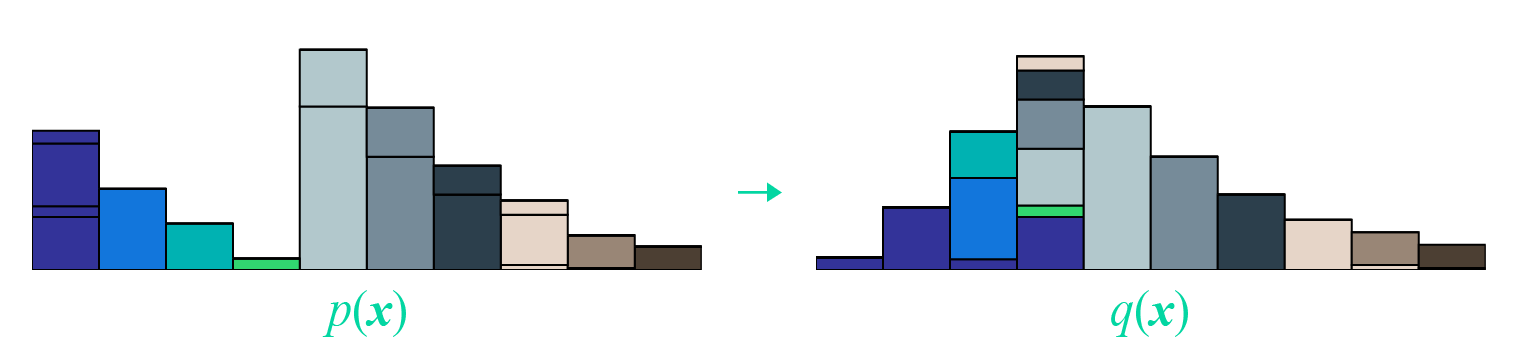
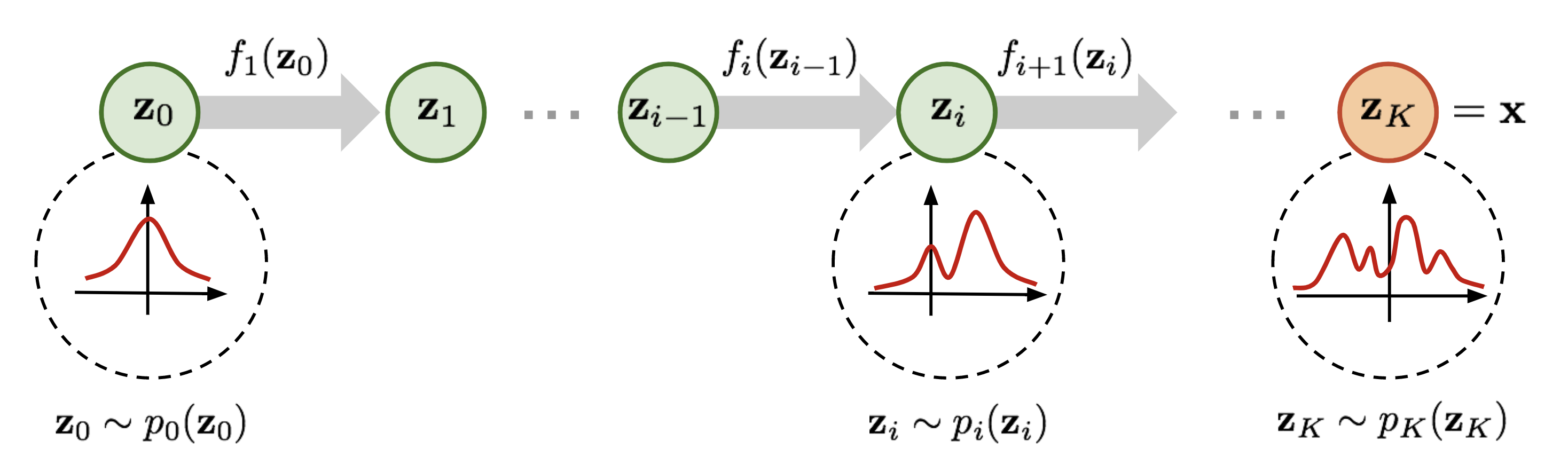
这是一篇尝试改变LLM「范式」的文章：当前主流的LLM架构都是「自回归」的，通俗地理解就是必须「从左到右依次生成」。这篇文章挑战了这一范式，探索扩散模型在 LLMs 上的可行性，通过 随机掩码 - 预测 的逆向思维，让模型学会「全局思考」。 论文： [2502.09992] Large Language Diffusion Models 背景 主流大语言模型架构：自回归模型 (Autoregressive LLMs) 过去几年， 自回归模型（Autoregressive Models, ARMs）一直是大语言模型(LLM)的主流架构​。典型的自回归语言模型以Transformer解码器为基础，按照从左到右 的顺序依次预测下一个词元(token)。 形式化地，自回归模型将一个长度为 \(N\) 的文本序列 \(X=(x_1, x_2, ..., x_N)\) 的概率分解为各位置的条件概率连乘积​： \[P_{\theta}(x_1, x_2, \dots, x_N) = \prod_{i=1}^{N} P_{\theta}(x_i \mid x_1, x_2, \dots,...

引言 Diffusion模型近年来在图像生成这一连续域任务中取得了显著成果，展现出强大的生成能力。然而，在文本生成这一离散域任务中整体效果仍不尽如人意，未能在该领域引起广泛关注。 去年，一篇研究离散扩散模型在文本生成的文章《Discrete Diffusion Modeling by Estimating the Ratios of the Data Distribution》获得ICML 2024的Best Paper，引发了学术界的广泛兴趣，也激发了新一轮的研究热潮。随后在2025年，越来越多高校和企业也开始积极探索基于Diffusion的文本生成方法。其中，近期备受关注的Block Diffusion也成功入选ICLR oral，进一步推动了该方向的发展。...

💡 扩散模型：通过加噪的方式去学习原始数据的分布， 从学到的分布中去生成样本 DDPM 关键点： 1. 正向加噪是离散时间马尔可夫链：从 \(x_0\) 逐步加噪得到 \(x_1,x_2,...,x_T\) ；在合适的噪声调度与足够大的 \(T\) 下， \(x_T\) 近似服从 \( N(0,I) \) 的各向同性高斯。 2. 每一步噪声方差 \(β_t\) 满足 \(0<β_t<1\) ，通常随 \(t\) 增大；因此 \(q(x_t|x_{t-1}) \) 的均值缩放系数 \(\sqrt{1-β_t} \) 逐渐减小。 3. 训练通过最大化对数似然的变分下界（ELBO）来学习反向过程 \( p_θ(x_{t-1}|x_t)\) ，并将其参数化为高斯分布（神经网络预测均值/噪声或 score）。 4. 将目标写成 score/DSM 形式时，loss 的权重与对应噪声层的方差尺度（如 \(1-\bar{α}_t\) 或相关量）有关；采样通常是按学习到的反向转移逐步生成（祖先采样），与经典 Langevin MCMC 更新形式不同，但可在 SDE 视角下统一理解。...

基于文章 《Elucidating the Design Space of Diffusion-Based Generative Models》 来统一扩散模型框架 通用扩散模型框架推导 加噪公式 Flow Matching的一步加噪公式 \[\mathbf{x}_t=(1-t)\mathbf{x}_0+t\varepsilon\] 写成概率分布形式： \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;(1-t)\mathbf{x}_0,t^2\mathbf{I})\] Score Matching的一步加噪公式 \[\mathbf{x}_t=\mathbf{x}_0+\sigma_t\varepsilon \] 写成概率分布形式： \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;\mathbf{x}_0,\sigma_t^2\mathbf{I})\] DDPM/DDIM的一步加噪公式...

2022年中旬，以扩散模型为核心的图像生成模型将AI绘画带入了大众的视野。实际上，在更早的一年之前，就有了一个能根据文字生成高清图片的模型——VQGAN。VQGAN不仅本身具有强大的图像生成能力，更是传承了前作VQVAE把图像压缩成离散编码的思想，推广了「先压缩，再生成」的两阶段图像生成思路，启发了无数后续工作。 VQGAN 核心思想 VQGAN的论文名为 Taming Transformers for High-Resolution Image Synthesis，直译过来是「驯服Transformer模型以实现高清图像合成」。可以看出，该方法是在用Transformer生成图像。可是，为什么这个模型叫做VQGAN，是一个GAN呢？这是因为，VQGAN使用了两阶段的图像生成方法： 训练时，先训练一个图像压缩模型（包括编码器和解码器两个子模型），再训练一个生成压缩图像的模型。 生成时， 先用第二个模型生成出一个压缩图像，再用第一个模型复原成真实图像 。 其中，第一个图像压缩模型叫做VQGAN，第二个压缩图像生成模型是一个基于Transformer的模型。...

本文受启发于著名的国外博文 《Wasserstein GAN and the Kantorovich-Rubinstein Duality》 ，内容跟它大体上相同，但是删除了一些冗余的部分，对不够充分或者含糊不清的地方作了补充。 Wasserstein距离 显然，整篇文章必然围绕着Wasserstein距离（ \(\mathcal{W}\) 距离）来展开。假设我们有了两个概率分布 \(p(x),q(x)\) ，那么Wasserstein距离的定义为 \[\mathcal{W}[p,q]=\inf_{\gamma\in \Pi[p,q]} \iint \gamma(\boldsymbol{x},\boldsymbol{y}) d(\boldsymbol{x},\boldsymbol{y}) d\boldsymbol{x}d\boldsymbol{y}\] 事实上，这也算是最优传输理论中最核心的定义了。 成本函数 首先 \(d(x,y)\) ，它不一定是距离，其准确含义应该是一个成本函数，代表着从 \(x\) 运输到 \(y\) 的成本。常用的 \(d\) 是基于 \(l\)...

简介 生成对抗网络 ( Generative Adversarial Network, GAN ) 是由 Goodfellow 于 2014 年提出的一种对抗网络。这个网络框架包含两个部分，一个生成模型 (generative model) 和一个判别模型 (discriminative model)。其中，生成模型可以理解为一个伪造者，试图通过构造假的数据骗过判别模型的甄别；判别模型可以理解为一个警察，尽可能甄别数据是来自于真实样本还是伪造者构造的假数据。两个模型都通过不断的学习提高自己的能力，即生成模型希望生成更真的假数据骗过判别模型，而判别模型希望能学习如何更准确的识别生成模型的假数据。 网络框架 GAN 由两部分构成，一个 生成器 ( Generator ) 和一个 判别器 ( Discriminator )。对于生成器，我们需要学习关于数据 \(x\) 的一个分布 \(p_g\) ，首先定义一个输入数据的先验分布 \(p_z(z)\) ，其次定义一个映射 \(G \left(\boldsymbol{z}; \theta_g\right): \boldsymbol{z}...

Normalizing flow（标准化流）是一类对概率分布进行建模的工具，它能完成简单的概率分布（例如高斯分布）和任意复杂分布之间的相互转换，经常被用于 data generation、density estimation、inpainting 等任务中，例如 Stability AI 提出的 Stable Diffusion 3 中用到的 rectified flow 就是 normalizing flow 的变体之一。 为了便于理解，在正式开始介绍之前先简要说明一下 normalizing flow 的做法。如上图所示，为了将一个高斯分布 \(z_0\) 转换为一个复杂的分布 \(z_K\) ，normalizing flow 会对初始的分布 \(z_0\) 进行多次可逆的变换，将其逐渐转换为 \(z_K\) 。由于每一次变换都是可逆的，从 \(z_K\) 出发也能得到高斯分布 \(z_0\) 。这样，我们就实现了复杂分布与高斯分布之间的互相转换，从而能从简单的高斯分布建立任意复杂分布。 对 diffusion models 比较熟悉的读者可能已经发现了，这个过程和...

背景 本文主要是《NICE: Nonlinear Independent Components Estimation》一文的介绍和实现。这篇文章也是glow这个模型的基础文章之一，可以说它就是glow的奠基石。 艰难的分布 众所周知，目前主流的生成模型包括VAE和GAN，但事实上除了这两个之外，还有基于flow的模型（flow可以直接翻译为“流”，它的概念我们后面再介绍）。事实上flow的历史和VAE、GAN它们一样悠久，但是flow却鲜为人知。在我看来，大概原因是flow找不到像GAN一样的诸如“造假者鉴别者”的直观解释吧，因为flow整体偏数学化，加上早期效果没有特别好但计算量又特别大，所以很难让人提起兴趣来。不过现在看来，OpenAI的这个好得让人惊叹的、基于flow的glow模型，估...

💡 原本随机采样的DDPM模型中，也隐含了一个确定性的采样过程DDIM，它的连续极限也是一个ODE。 细想上述过程，可以发现不管是“DDPM→DDIM”还是“SDE→ODE”，都是从随机采样模型过渡到确定性模型，而如果我们一开始的目标就是ODE，那么该过程未免显得有点“迂回”了。在本文中，笔者尝试给出ODE扩散模型的直接推导，并揭示了它与雅可比行列式、热传导方程等内容的联系。 Rectified Flow 理论推导 微分方程 像GAN这样的生成模型，它本质上是希望找到一个确定性变换，能将从简单分布（如标准正态分布）采样出来的随机变量，变换为特定数据分布的样本。flow模型也是生成模型之一，它的思路是反过来，先找到一个能将数据分布变换简单分布的可逆变换，再求解相应的逆变换来得到一个生成模型。 ...