INCOMING TRANSMISSION

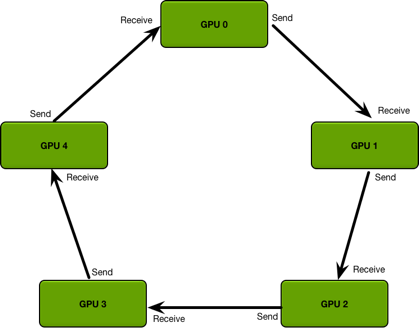
Quick Start 一个最简单的DDP Pytorch例子！ 环境准备 PyTorch(gpu)=1.5，python=3.6 推荐使用官方打好的PyTorch docker，避免乱七八糟的环境问题影响心情。 [代码] 代码 单GPU代码 [代码] 加入DDP的代码 [代码] DDP的基本原理 大白话原理 假如我们有N张显卡， 1. （缓解GIL限制）在DDP模式下，会有N个进程被启动，每个进程在一张卡上加载一个模型，这些模型的参数在数值上是相同的。 1. （RingReduce加速）在模型训练时，各个进程通过一种叫RingReduce的方法与其他进程通讯，交换各自的梯度，从而获得所有进程的梯度； 1. （实际上就是Data Parallelism）各个进程用平均后的梯度更新自己的参数，...

@tf_export为函数取了个名字！ Tensorflow经常看到定义的函数前面加了@tf_export。例如，tensorflow/python/platform/app.py中有： [代码] 首先，@tf_export是一个修饰符。修饰符的本质是一个函数 tf_export的实现在tensorflow/python/util/tf_export.py中： [代码] 等号的右边的理解分两步： 1. functools.partial 1. api_export functools.partial是偏函数,它的本质简而言之是为函数固定某些参数。如：functools.partial(FuncA, p1)的作用是把函数FuncA的第一个参数固定为p1；又如functools.partial(...

问题表示 有很多概率问题，尤其是独立重复实验问题，如果用生成函数的方法来做，会显得特别方便。本文要讲的“随机游走”问题便是其中一例，它又被形象地叫做“醉汉问题”，其本质上是一个二项分布，但是由于取了极限，出现了很多新的性质和应用。我们先考虑如下问题： 考虑实数轴上的一个粒子，在 t=0 时刻它位于原点，每过一秒，它要不向前移动一格（+1），要不就向后移动一格（1），问 n 秒后它所处位置的概率分布。 不难发现，这个问题跟二项分布是雷同的。如果把这个粒子形象比喻成一个“喝醉酒的人”，那么上面的走法就类似于一个完全不省人事的醉汉走路问题了。（当然，醉汉是在三维空间走路的，这里简单起见，只描述了一维...

引言与背景 FlashAttention的关键创新在于使用类似于在线Softmax的思想来对自注意力计算进行分块（tiling），从而能够融合整个多头注意力层的计算，而无需访问GPU全局内存来存储中间的logits和注意力分数 在深度学习中，Transformer模型的自注意力机制是计算密集型操作。传统实现需要在GPU全局内存中存储大量中间结果，这导致： 内存瓶颈：中间矩阵占用大量显存 I/O开销：频繁的全局内存访问降低效率 扩展性限制：难以处理超长序列 FlashAttention通过算法创新解决了这些问题。 SelfAtention 自注意力机制的计算可以总结为（为简化说明，忽略头数和批次维度，也省略注意力掩码和缩放因子 [Math] ）： [公式] 其中： Q, K, V, O 都是形...

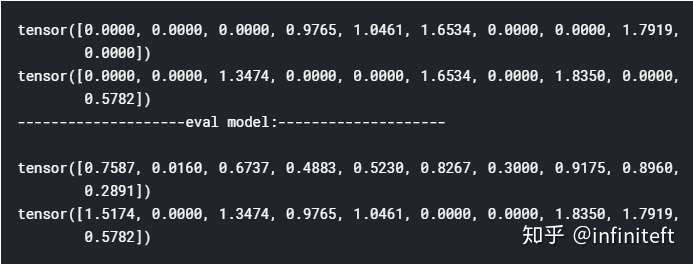
PyTorch中，所有神经网络的核心是 autograd 包。 autograd 包为张量上的所有操作提供了自动求导机制。它是一个在运行时定义(definebyrun）的框架，这意味着反向传播是根据代码如何运行来决定的，并且每次迭代可以是不同的. 让我们用一些简单的例子来看看吧。 张量 torch.Tensor 是这个包的核心类。如果设置它的属性 .requires_grad 为 True，那么它将会追踪对于该张量的所有操作。当完成计算后可以通过调用 .backward()，来自动计算所有的梯度。这个张量的所有梯度将会自动累加到.grad属性. 要阻止一个张量被跟踪历史，可以调用 .detach() 方法将其与计算历史分离，并阻止它未来的计算记录被跟踪。 为了防止跟踪历史记录(和使用内存），...

相同点 nn.Xxx和nn.functional.xxx的实际功能是相同的，即nn.Conv2d和nn.functional.conv2d 都是进行卷积，nn.Dropout 和nn.functional.dropout都是进行dropout，。。。。。； 运行效率也是近乎相同。 nn.functional.xxx是函数接口，而nn.Xxx是nn.functional.xxx的类封装，并且nn.Xxx都继承于一个共同祖先nn.Module。这一点导致nn.Xxx除了具有nn.functional.xxx功能之外，内部附带了nn.Module相关的属性和方法，例如train(), eval(),load_state_dict, state_dict 等。 不同点 两者的调用方式不同。 nn.X...

问题定义 多元二次多项式，维度为 n ，那么可以用以下公式描述该函数： [Formula] 其中 a_{i,j} 为二次项系数，共有 n^2 项， 1≤i,j≤n ，且所有的 a 不全为0，即 ∃a_{i,j}≠0 ; b_k 为一次项系数，共 n 项， 1≤k≤n ; c 为常数项。 记 f(x)=[x_1,x_2,...,x_n]^T ，则上述函数可以写作二次型的形式： 转化过程中A,b满足： A 为n阶对称方阵， A_{i,j}=a_{i,j} 因为 ∃a_{i,j}≠0 ，A不为零矩阵 b_i=b_i 为了后续计算简便，我们将二次型稍作改动： [Formula] 我们的目标就是寻找该函...

基本概念 方向导数：是一个数；反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 偏导数：是多个数（每元有一个）；是指多元函数沿坐标轴方向的方向导数，因此二元函数就有两个偏导数。 偏导函数：是一个函数；是一个关于点的偏导数的函数。 梯度：是一个向量；每个元素为函数对一元变量的偏导数；它既有大小（其大小为最大方向导数），也有方向。 方向导数 反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 例子如下： 题目 设二元函数 f(x, y) = x^2 + y^2 ，分别计算此函数在点 (1, 2) 沿方向 w=\{3, 4\} 与方向 u=\{1, 0\} 的方向导数。 解： ...

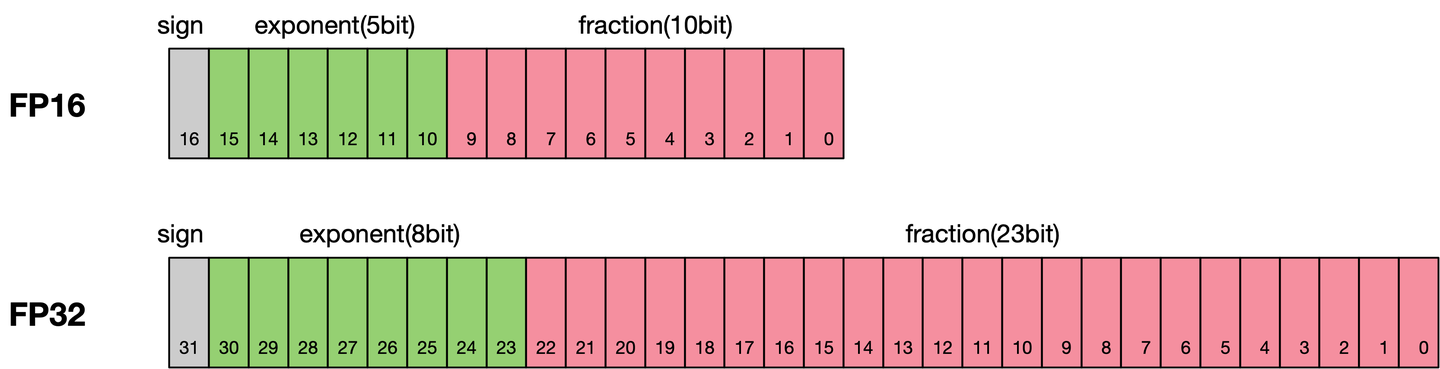
通常我们训练神经网络模型的时候默认使用的数据类型为单精度FP32。近年来，为了加快训练时间、减少网络训练时候所占用的内存，并且保存训练出来的模型精度持平的条件下，业界提出越来越多的混合精度训练的方法。这里的混合精度训练是指在训练的过程中，同时使用单精度（FP32）和半精度（FP16）。 浮点数据类型 浮点数据类型主要分为双精度（FP64）、单精度（FP32）、半精度（FP16）。在神经网络模型的训练过程中，一般默认采用单精度（FP32）浮点数据类型，来表示网络模型权重和其他参数。在了解混合精度训练之前，这里简单了解浮点数据类型。 根据IEEE二进制浮点数算术标准（IEEE 754）的定义，浮点数据类型分为双精度（FP64）、单精度（FP32）、半精度（FP16）三种，其中每一种都有三个不同的...

概述 Medusa 是自投机领域较早的一篇工作，对后续工作启发很大，其主要思想是 multidecoding head + tree attention + typical acceptance(threshold)。Medusa 没有使用独立的草稿模型，而是在原始模型的基础上增加多个解码头（MEDUSA heads），并行预测多个后续 token。 正常的LLM只有一个用于预测 t 时刻token的head。Medusa 在 LLM 的最后一个 Transformer层之后保留原始的 LM Head，然后额外增加多个（假设是 k 个） 可训练的Medusa Head（解码头），分别负责预测 ...

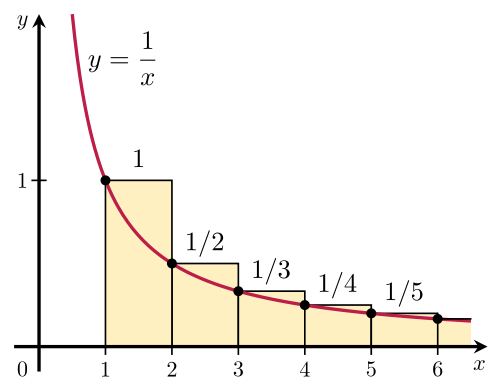
调和级数记住下面的公式就够了： [Formula] 证明方法就是下面这张图

一、泊松分布 日常生活中，大量事件是有固定频率的。 某医院平均每小时出生3个婴儿 某公司平均每10分钟接到1个电话 某超市平均每天销售4包xx牌奶粉 某网站平均每分钟有2次访问 它们的特点就是，我们可以预估这些事件的总数，但是没法知道具体的发生时间。已知平均每小时出生3个婴儿，请问下一个小时，会出生几个？ 有可能一下子出生6个，也有可能一个都不出生。这是我们没法知道的。 泊松分布就是描述某段时间内，事件具体的发生概率。 [Formula] 上面就是泊松分布的公式。等号的左边， P 表示概率， N 表示某种函数关系， t 表示时间， n 表示数量，1小时内出生3个婴儿的概率，就表示为 P(N(1...