INCOMING TRANSMISSION

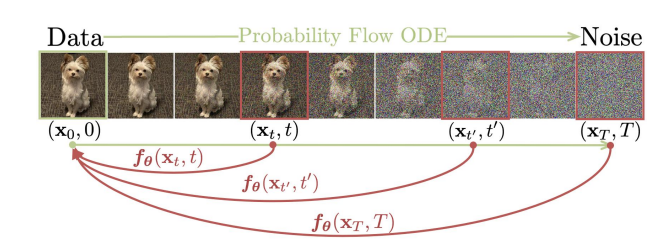
基于文章 《Elucidating the Design Space of Diffusion-Based Generative Models》 来统一扩散模型框架 通用扩散模型框架推导 加噪公式 Flow Matching的一步加噪公式 \[\mathbf{x}_t=(1-t)\mathbf{x}_0+t\varepsilon\] 写成概率分布形式： \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;(1-t)\mathbf{x}_0,t^2\mathbf{I})\] Score Matching的一步加噪公式 \[\mathbf{x}_t=\mathbf{x}_0+\sigma_t\varepsilon \] 写成概率分布形式： \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;\mathbf{x}_0,\sigma_t^2\mathbf{I})\] DDPM/DDIM的一步加噪公式...

简介 后训练（post-training）已成为完整训练流程中的重要组成部分。相比于预训练，后训练需要的计算资源相对较少，但能够： 提高推理任务的准确性 使模型与社会价值观保持一致 适应用户偏好 OpenAI 的 o1 系列模型首次引入了通过增加思维链（Chain-of-Thought）推理过程长度来实现推理时间，扩展这种方法在数学、编程和科学推理等各种推理任务上取得了显著改进 研究界已探索多种方法来提高模型的推理能力：比如 基于过程的奖励模型 （Process-based Reward Models） 强化学习 （Reinforcement Learning）, 代表工作：InstructGPT， 以及 搜索算法（ 蒙特卡洛树搜索（Monte Carlo Tree Search）、束搜索（Beam Search））。然而，这些方法尚未达到与 OpenAI o1 系列模型相当的通用推理性能。 DeepSeek-R1-Zero 本文首先探索使用纯强化学习（RL）来提高语言模型的推理能力，重点关注： 探索 LLM 在没有任何监督数据的情况下，通过纯 RL 过程的自我进化来发展推理能力...

Diffusion Models from SDE 连续扩散模型 (Continuous Diffusion Models) 将传统的离散时间扩散过程扩展到连续时间域,可以被视为一个随机过程，使用随机微分方程(SDE)来描述。其前向过程可以写成如下形式： [公式] 其中， f(x,t) 可以看成偏移系数， g(t) 可以看成是扩散系数， dw 是标准布朗运动。这个SDE 描述了数据在连续时间域内如何被噪声逐渐破坏。 这个随机过程的逆向过程存在（更准确的描述：下面的逆向时间SDE具有与正向过程SDE相同的联合分布）为 [公式] 前面我们得到了扩散过程的逆向过程可以用一个SDE描述(逆向随机过程),事实上，存在一个确定性过程 (用ODE描述)也是它的逆向过程 (更准确的描述：这个ODE过程的在任...

问题表示 有很多概率问题，尤其是独立重复实验问题，如果用生成函数的方法来做，会显得特别方便。本文要讲的“随机游走”问题便是其中一例，它又被形象地叫做“醉汉问题”，其本质上是一个二项分布，但是由于取了极限，出现了很多新的性质和应用。我们先考虑如下问题： 考虑实数轴上的一个粒子，在 t=0 时刻它位于原点，每过一秒，它要不向前移动一格（+1），要不就向后移动一格（1），问 n 秒后它所处位置的概率分布。 不难发现，这个问题跟二项分布是雷同的。如果把这个粒子形象比喻成一个“喝醉酒的人”，那么上面的走法就类似于一个完全不省人事的醉汉走路问题了。（当然，醉汉是在三维空间走路的，这里简单起见，只描述了一维...

引言与背景 随机逼近（Stochastic Approximation）是一类用于求解寻根或优化问题的随机迭代算法，其特点是不需要知道目标函数或其导数的表达式。 随机逼近的核心优势在于： 能够处理带有随机噪声的观测数据 不需要目标函数的解析表达式 可以在线学习，每获得一个新样本就更新估计值 均值估计问题 考虑一个随机变量 X ，其取值来自有限集合 [Math] 。我们的目标是估计 E[X] 。假设我们有一个独立同分布的样本序列 \{x_i\}_{i=1}^n ，那么 X 的期望值可以近似为： [公式] 非增量方法与增量方法 非增量方法：先收集所有样本，然后计算平均值。缺点是如果样本数量很大，可能需要等待很长时间。 增量方法：定义 [公式] 可以推导出递归公式： [公式] 这个算法可以增量式地...

引言与背景 蒙特卡洛方法是强化学习中的重要算法类别，它标志着从基于模型到无模型算法的转变。这类算法不依赖环境模型，而是通过与环境的直接交互获取经验数据来学习最优策略。 蒙特卡洛方法在强化学习算法谱系中处于"无模型"方法的起始位置，是从基于模型的方法（如值迭代和策略迭代）向无模型方法过渡的第一步。 无模型强化学习的核心理念可以简述为：如果没有模型，我们必须有数据；如果没有数据，我们必须有模型；如果两者都没有，我们就无法找到最优策略。在强化学习中，"数据"通常指智能体与环境交互的经验。 均值估计问题 在介绍蒙特卡洛强化学习算法之前，我们首先需要理解均值估计问题，这是理解从数据而非模型中学习的基础。 考虑一个可以取有限实数集合 X 中值的随机变量 X ，我们的任务是计算 X 的均值或期望值： E[...

基础概念 GridWord Example 环境描述：网格世界是一个直观的二维环境，包含： 任务目标： 什么是强化学习：依据策略执行动作感知状态得到奖励 所谓强化学习(Reinforcement Learning，简称RL)，是指基于智能体在复杂、不确定的环境中最大化它能获得的奖励，从而达到自主决策的目的。 a computational approach to learning whereby an agent tries to maximize the total amount of reward it receives while interacting with a complex and uncertain environment 经典的强化学习模型可以总结为下图的形式（你可以理解...

背景 RLHF 通常包括三个阶段： 有监督微调（SFT） 奖励建模阶段 （Reward Model） RL微调阶段 直接偏好优化（DPO） 传统的RLHF方法分两步走： 1. 先训练一个奖励模型来判断哪个回答更好 1. 然后用强化学习让语言模型去最大化这个奖励 这个过程很复杂，就像绕了一大圈：先学习"什么是好的"，再学习"如何做好"。 DPO发现了一个数学上的捷径： 1. 关键发现：对于任何奖励函数，都存在一个对应的最优策略（语言模型）；反过来说，任何语言模型也隐含着一个它认为最优的奖励函数 1. 直接优化：与其先训练奖励模型再训练语言模型，不如直接训练语言模型，让它自己内化"什么是好的" 1. 数学转换：DPO将"学习判断好坏"和"学习生成好内容"这两个任务合二为一，通过一个简单的数学变换...

模型概述 KimiVL 是一个高效的开源混合专家视觉语言模型(VLM)，它提供先进的多模态推理、长上下文理解和强大的代理能力，同时在语言解码器中仅激活 2.8B 参数(KimiVLA3B)。该模型在多种挑战性任务中表现出色，包括一般用途的视觉语言理解、多轮代理任务、大学水平的图像和视频理解、OCR、数学推理和多图像理解等. 模型架构 KimiVL 的架构由三个主要部分组成： MoE语言模型 Moonlight MoE language model with only 2.8B activated (16B total) parameters 视觉模型 400M nativeresolution MoonViT vision encoder. MLP Projector MoonViT: 原生...

💡 Score based generative model SMLD的关键点： 正式开始介绍之前首先解答一下这个问题：scorebased 模型是什么东西，微分方程在这个模型里到底有什么用？我们知道生成模型基本都是从某个现有的分布中进行采样得到生成的样本，为此模型需要完成对分布的建模。根据建模方式的不同可以分为隐式建模（例如 GAN、diffusion models）和显式建模（例如 VAE、normalizing flows）。和上述的模型相同，scorebased 模型也是用一定方式对分布进行了建模。具体而言，这类模型建模的对象是概率分布函数 log 的梯度，也就是 score function，而为了对这个建模对象进行学习，需要使用一种叫做 score matching 的技术，这也...

引言 DDPG同样使用了ActorCritic的结构，Deterministic的确定性策略是和随机策略相对而言的，对于某一些动作集合来说，它可能是连续值，或者非常高维的离散值，这样动作的空间维度极大。如果我们使用随机策略，即像DQN一样研究它所有的可能动作的概率，并计算各个可能的动作的价值的话，那需要的样本量是非常大才可行的。于是有人就想出使用确定性策略来简化这个问题。 作为随机策略，在相同的策略，在同一个状态 s 处，采用的动作 [Math] 是基于一个概率分布的，即是不确定的。而确定性策略则决定简单点，虽然在同一个状态处，采用的动作概率不同，但是最大概率只有一个，如果我们只取最大概率的动作，去掉这个概率分布，那么就简单多了。即作为确定性策略，相同的策略，在同一个状态处，动作是唯一确定的...

问题定义 多元二次多项式，维度为 n ，那么可以用以下公式描述该函数： [Formula] 其中 a_{i,j} 为二次项系数，共有 n^2 项， 1≤i,j≤n ，且所有的 a 不全为0，即 ∃a_{i,j}≠0 ; b_k 为一次项系数，共 n 项， 1≤k≤n ; c 为常数项。 记 f(x)=[x_1,x_2,...,x_n]^T ，则上述函数可以写作二次型的形式： 转化过程中A,b满足： A 为n阶对称方阵， A_{i,j}=a_{i,j} 因为 ∃a_{i,j}≠0 ，A不为零矩阵 b_i=b_i 为了后续计算简便，我们将二次型稍作改动： [Formula] 我们的目标就是寻找该函...