INCOMING TRANSMISSION

128. 最长连续序列 题目 给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 1： 输入：nums = [100,4,200,1,3,2] 输出：4 解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。 示例 2： 输入：nums = [0,3,7,2,5,8,4,6,0,1] 输出：9 示例 3： 输入：nums = [1,0,1,2] 输出：3 提示： 0 <= nums.length <= 10 5 -10 9 <= nums[i] <= 10 9 题解 我们需要在 \(O(1)\) 的时间内查找某个数是否存在。因此，首先将数组中的所有元素放入一个 HashSet 中。这不仅能去重，还能支持快速查找。 避免冗余计算 (关键优化) 如果我们对集合中的每一个数都尝试去向后计数（例如，对于 x ，尝试找 x+1 , x+2 ...），最坏情况下的时间复杂度会退化到 \(O(n^2)\) 。 优化策略 ： 我们 只从序列的起点开始计数 。...

76. 最小覆盖子串 题目 给定两个字符串 s 和 t ，长度分别是 m 和 n ，返回 s 中的 最短窗口 子串 ，使得该子串包含 t 中的每一个字符（ 包括重复字符 ）。如果没有这样的子串，返回空字符串 "" 。 测试用例保证答案唯一。 示例 1： 输入：s = "ADOBECODEBANC", t = "ABC" 输出："BANC" 解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。 示例 2： 输入：s = "a", t = "a" 输出："a" 解释：整个字符串 s 是最小覆盖子串。 示例 3: 输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中， 因此没有符合条件的子字符串，返回空字符串。 提示： m == s.length n == t.length 1 <= m, n <= 10 5 s 和 t 由英文字母组成 题解 这是一个经典的 滑动窗口 (Sliding Window) 问题 我们需要维护一个动态的窗口 [left, right] ： 右移扩大 ：不断移动...

基于文章 《Elucidating the Design Space of Diffusion-Based Generative Models》 来统一扩散模型框架 通用扩散模型框架推导 加噪公式 Flow Matching的一步加噪公式 \[\mathbf{x}_t=(1-t)\mathbf{x}_0+t\varepsilon\] 写成概率分布形式： \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;(1-t)\mathbf{x}_0,t^2\mathbf{I})\] Score Matching的一步加噪公式 \[\mathbf{x}_t=\mathbf{x}_0+\sigma_t\varepsilon \] 写成概率分布形式： \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;\mathbf{x}_0,\sigma_t^2\mathbf{I})\] DDPM/DDIM的一步加噪公式...

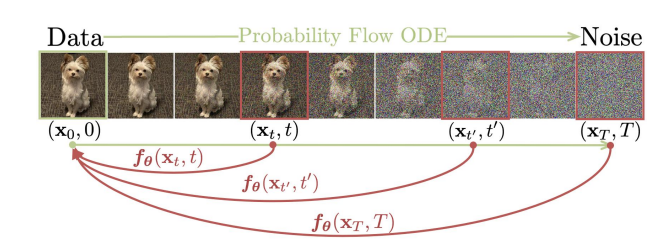
Diffusion Models from SDE 连续扩散模型 (Continuous Diffusion Models) 将传统的离散时间扩散过程扩展到连续时间域,可以被视为一个随机过程，使用随机微分方程(SDE)来描述。其前向过程可以写成如下形式： [公式] 其中， f(x,t) 可以看成偏移系数， g(t) 可以看成是扩散系数， dw 是标准布朗运动。这个SDE 描述了数据在连续时间域内如何被噪声逐渐破坏。 这个随机过程的逆向过程存在（更准确的描述：下面的逆向时间SDE具有与正向过程SDE相同的联合分布）为 [公式] 前面我们得到了扩散过程的逆向过程可以用一个SDE描述(逆向随机过程),事实上，存在一个确定性过程 (用ODE描述)也是它的逆向过程 (更准确的描述：这个ODE过程的在任...

问题表示 有很多概率问题，尤其是独立重复实验问题，如果用生成函数的方法来做，会显得特别方便。本文要讲的“随机游走”问题便是其中一例，它又被形象地叫做“醉汉问题”，其本质上是一个二项分布，但是由于取了极限，出现了很多新的性质和应用。我们先考虑如下问题： 考虑实数轴上的一个粒子，在 t=0 时刻它位于原点，每过一秒，它要不向前移动一格（+1），要不就向后移动一格（1），问 n 秒后它所处位置的概率分布。 不难发现，这个问题跟二项分布是雷同的。如果把这个粒子形象比喻成一个“喝醉酒的人”，那么上面的走法就类似于一个完全不省人事的醉汉走路问题了。（当然，醉汉是在三维空间走路的，这里简单起见，只描述了一维...

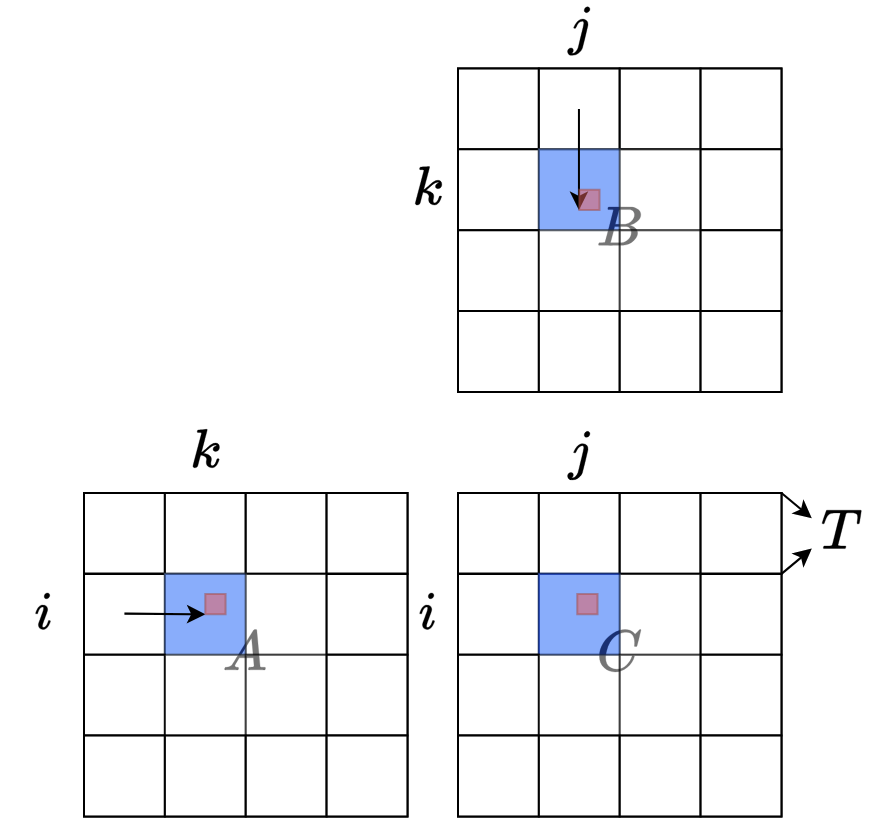
引言与背景 FlashAttention的关键创新在于使用类似于在线Softmax的思想来对自注意力计算进行分块（tiling），从而能够融合整个多头注意力层的计算，而无需访问GPU全局内存来存储中间的logits和注意力分数 在深度学习中，Transformer模型的自注意力机制是计算密集型操作。传统实现需要在GPU全局内存中存储大量中间结果，这导致： 内存瓶颈：中间矩阵占用大量显存 I/O开销：频繁的全局内存访问降低效率 扩展性限制：难以处理超长序列 FlashAttention通过算法创新解决了这些问题。 SelfAtention 自注意力机制的计算可以总结为（为简化说明，忽略头数和批次维度，也省略注意力掩码和缩放因子 [Math] ）： [公式] 其中： Q, K, V, O 都是形...

💡 Score based generative model SMLD的关键点： 正式开始介绍之前首先解答一下这个问题：scorebased 模型是什么东西，微分方程在这个模型里到底有什么用？我们知道生成模型基本都是从某个现有的分布中进行采样得到生成的样本，为此模型需要完成对分布的建模。根据建模方式的不同可以分为隐式建模（例如 GAN、diffusion models）和显式建模（例如 VAE、normalizing flows）。和上述的模型相同，scorebased 模型也是用一定方式对分布进行了建模。具体而言，这类模型建模的对象是概率分布函数 log 的梯度，也就是 score function，而为了对这个建模对象进行学习，需要使用一种叫做 score matching 的技术，这也...

问题定义 多元二次多项式，维度为 n ，那么可以用以下公式描述该函数： [Formula] 其中 a_{i,j} 为二次项系数，共有 n^2 项， 1≤i,j≤n ，且所有的 a 不全为0，即 ∃a_{i,j}≠0 ; b_k 为一次项系数，共 n 项， 1≤k≤n ; c 为常数项。 记 f(x)=[x_1,x_2,...,x_n]^T ，则上述函数可以写作二次型的形式： 转化过程中A,b满足： A 为n阶对称方阵， A_{i,j}=a_{i,j} 因为 ∃a_{i,j}≠0 ，A不为零矩阵 b_i=b_i 为了后续计算简便，我们将二次型稍作改动： [Formula] 我们的目标就是寻找该函...

基本概念 方向导数：是一个数；反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 偏导数：是多个数（每元有一个）；是指多元函数沿坐标轴方向的方向导数，因此二元函数就有两个偏导数。 偏导函数：是一个函数；是一个关于点的偏导数的函数。 梯度：是一个向量；每个元素为函数对一元变量的偏导数；它既有大小（其大小为最大方向导数），也有方向。 方向导数 反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 例子如下： 题目 设二元函数 f(x, y) = x^2 + y^2 ，分别计算此函数在点 (1, 2) 沿方向 w=\{3, 4\} 与方向 u=\{1, 0\} 的方向导数。 解： ...

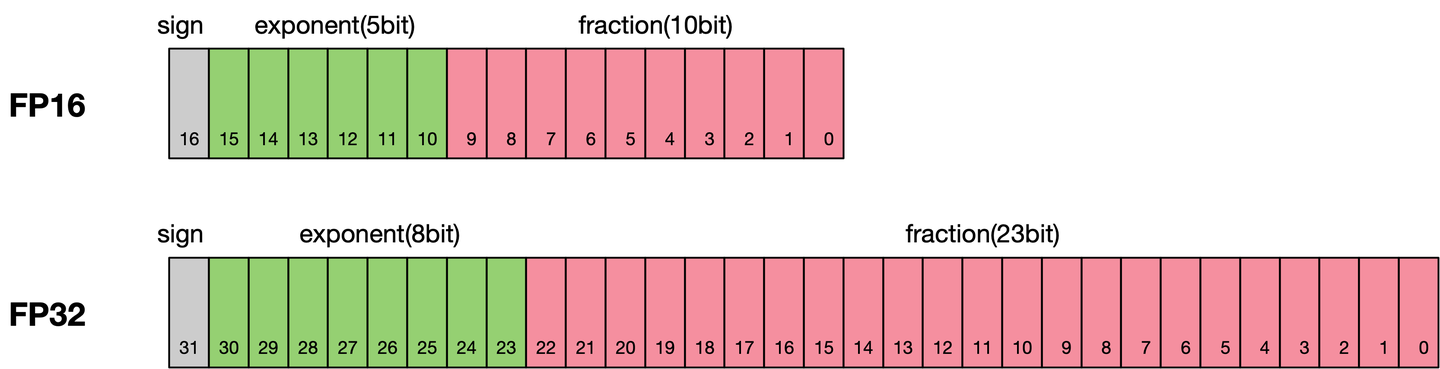
通常我们训练神经网络模型的时候默认使用的数据类型为单精度FP32。近年来，为了加快训练时间、减少网络训练时候所占用的内存，并且保存训练出来的模型精度持平的条件下，业界提出越来越多的混合精度训练的方法。这里的混合精度训练是指在训练的过程中，同时使用单精度（FP32）和半精度（FP16）。 浮点数据类型 浮点数据类型主要分为双精度（FP64）、单精度（FP32）、半精度（FP16）。在神经网络模型的训练过程中，一般默认采用单精度（FP32）浮点数据类型，来表示网络模型权重和其他参数。在了解混合精度训练之前，这里简单了解浮点数据类型。 根据IEEE二进制浮点数算术标准（IEEE 754）的定义，浮点数据类型分为双精度（FP64）、单精度（FP32）、半精度（FP16）三种，其中每一种都有三个不同的...

概述 Medusa 是自投机领域较早的一篇工作，对后续工作启发很大，其主要思想是 multidecoding head + tree attention + typical acceptance(threshold)。Medusa 没有使用独立的草稿模型，而是在原始模型的基础上增加多个解码头（MEDUSA heads），并行预测多个后续 token。 正常的LLM只有一个用于预测 t 时刻token的head。Medusa 在 LLM 的最后一个 Transformer层之后保留原始的 LM Head，然后额外增加多个（假设是 k 个） 可训练的Medusa Head（解码头），分别负责预测 ...

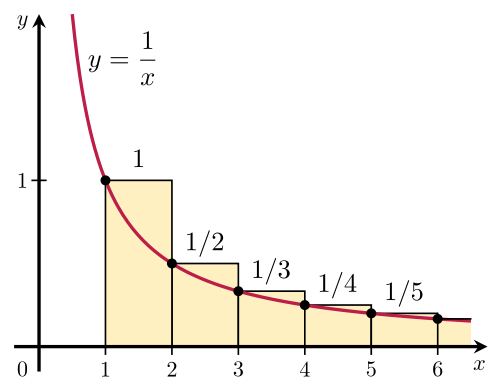
调和级数记住下面的公式就够了： [Formula] 证明方法就是下面这张图