INCOMING TRANSMISSION

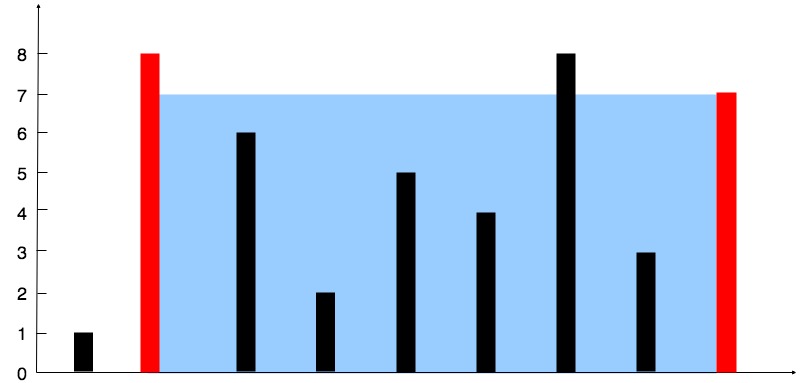
11. 盛最多水的容器 题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明： 你不能倾斜容器。 示例 1： 输入：[1,8,6,2,5,4,8,3,7] 输出：49 解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。 示例 2： 输入：height = [1,1] 输出：1 提示： n == height.length 2 <= n <= 10 5 0 <= height[i] <= 10 4 题解 在初始时，左右指针分别指向数组的左右两端，它们可以容纳的水量为 \(min(1,7)∗8=8\) 。 此时我们需要移动一个指针。移动哪一个呢？直觉告诉我们，应该移动对应数字较小的那个指针（即此时的左指针）。这是因为，由于容纳的水量是由 两个指针指向的数字中较小值∗指针之间的距离...

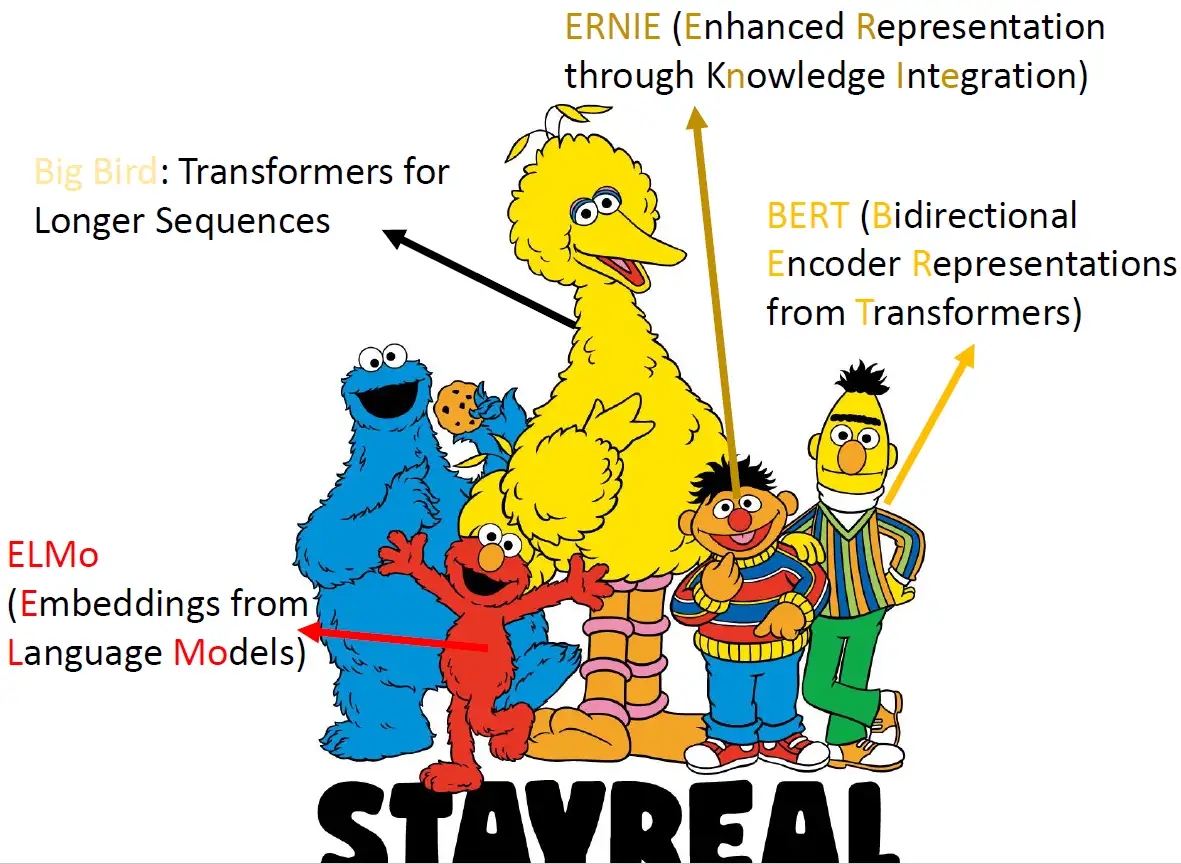
Self-Supervised Learning ，又称为自监督学习，我们知道一般机器学习分为有监督学习，无监督学习和强化学习。 而 Self-Supervised Learning 是无监督学习里面的一种，主要是希望能够学习到一种 通用的特征表达 用于 下游任务 (Downstream Tasks) 。 其主要的方式就是通过自己监督自己。作为代表作的 kaiming 的 MoCo 引发一波热议， Yann Lecun也在 AAAI 上讲 Self-Supervised Learning 是未来的大势所趋。所以在这个系列中，我会系统地解读 Self-Supervised Learning 的经典工作。 本文主要介绍 Self-Supervised Learning 在 NLP领域 的经典工作：BERT模型的原理及其变体。 本文来自台湾大学李宏毅老师PPT： https://speech.ee.ntu.edu.tw/~hylee/ml/ml2021-course-data/bert_v8.pdf 芝麻街 在介绍 Self-Supervised Learning...

简介 如果以概率的视角看待世界的生成模型。 在这样的世界观中，我们可以将任何类型的观察数据（例如 \(D\) ）视为来自底层分布（例如 \( p_{data}\) ）的有限样本集。 任何生成模型的目标都是在访问数据集 \(D\) 的情况下近似该数据分布。 如果我们能够学习到一个好的生成模型，我们可以将学习到的模型用于下游推理。 我们主要对数据分布的参数近似感兴趣，在一组有限的参数中，它总结了关于数据集 \(D\) 的所有信息。 与非参数模型相比，参数模型在处理大型数据集时能够更有效地扩展，但受限于可以表示的分布族。 在参数的设置中，我们可以将学习生成模型的任务视为在模型分布族中挑选参数，以最小化模型分布和数据分布之间的距离。 如上图，给定一个狗的图像数据集，我们的目标是学习模型族 \(M\) 中生成模型 θ 的参数，使得模型分布 \(p_θ\) 接近 \(p_{data}\) 上的数据分布。 在数学上，我们可以将我们的目标指定为以下优化问题: \[\mathop{min}\limits_{\theta\in M}d(p_\theta,p_{data})\] 其中， \(d()\)...

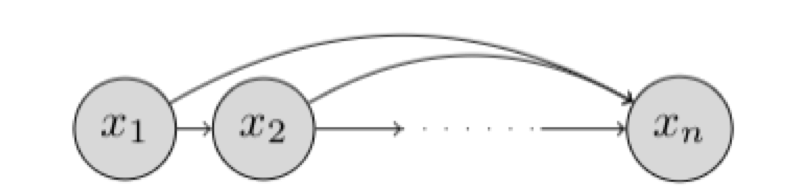
研究对象与基本设定 我们希望学习一个能够“生成数据”的概率模型。假设我们有一个数据集 \(D\) ，每个样本是 \(n\) 维二值向量： \(x \in \{0,1\}^n\) 我们的目标是用一个参数化分布 \(p_\theta(x)\) 去逼近真实数据分布 \(p_{\text{data}}(x)\) ，并最终能够： 密度估计 ：给定 \(x\) 计算 \(p_\theta(x)\) 或 \(\log p_\theta(x)\) 采样生成 ：从 \(p_\theta(x)\) 采样得到新的 \(x\) 表示：链式法则与自回归分解 链式法则分解联合分布 任意联合分布都可用概率链式法则分解为条件概率的乘积： \[p(x) = \prod_{i=1}^{n} p(x_i \mid x_1, x_2, \dots, x_{i-1}) = \prod_{i=1}^{n} p(x_i \mid x_{<i})\] 其中： \(x_{<i} = [x_1, x_2, \dots, x_{i-1}]\) ，这意味着：只要我们能为每个维度 \(i\) 学好一个条件分布 \(p(x_i \mid...

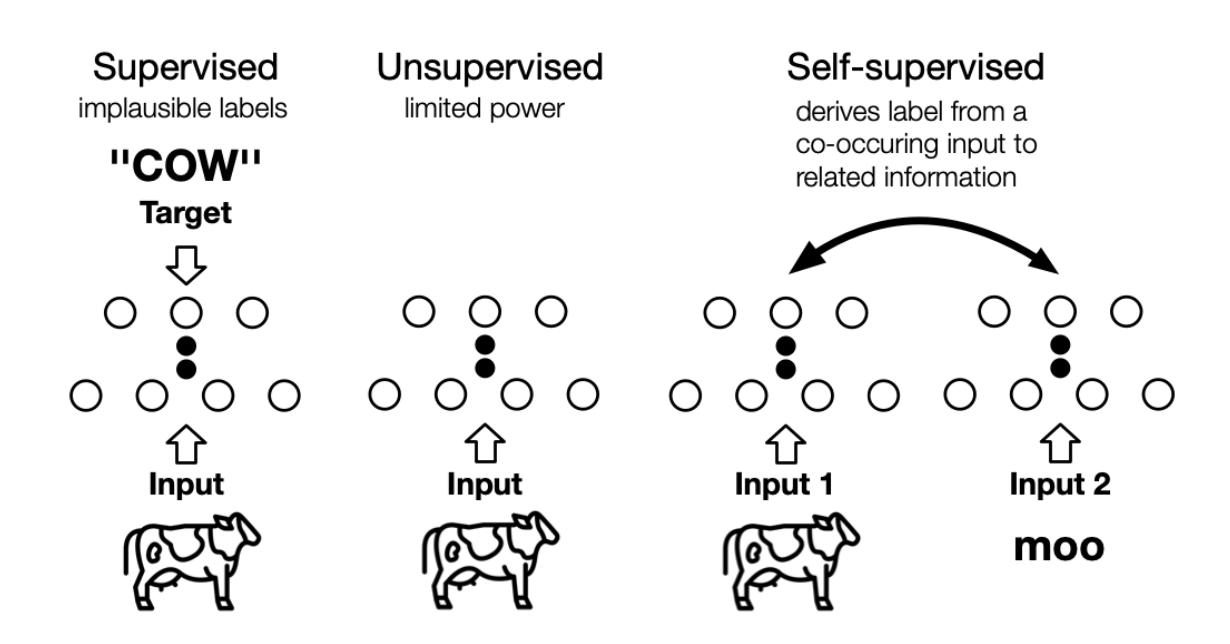
the machine predicts any parts of its input for any observed part 这是LeCun在AAAI 2020上对自监督学习的定义，再结合传统的自监督学习定义，可以总结如下两点特征： 通过“半自动”过程从数据本身获取“标签”； 从“其他部分”预测部分数据。 个人理解， 其实任意挖掘对象之间联系、探索不同对象共同本质的方法，都或多或少算是自监督学习的思想 。 自监督学习与无监督学习的区别主要在于，无监督学习专注于检测特定的数据模式，如聚类、社区发现或异常检测，而自监督学习的目标是恢复（recovering），仍处于监督学习的范式中。上图展示了三者之间的区别， 自监督中的“related information” 可以来自其他模态、输入的其他部分以及输入的不同形式。 Self-Supervised...

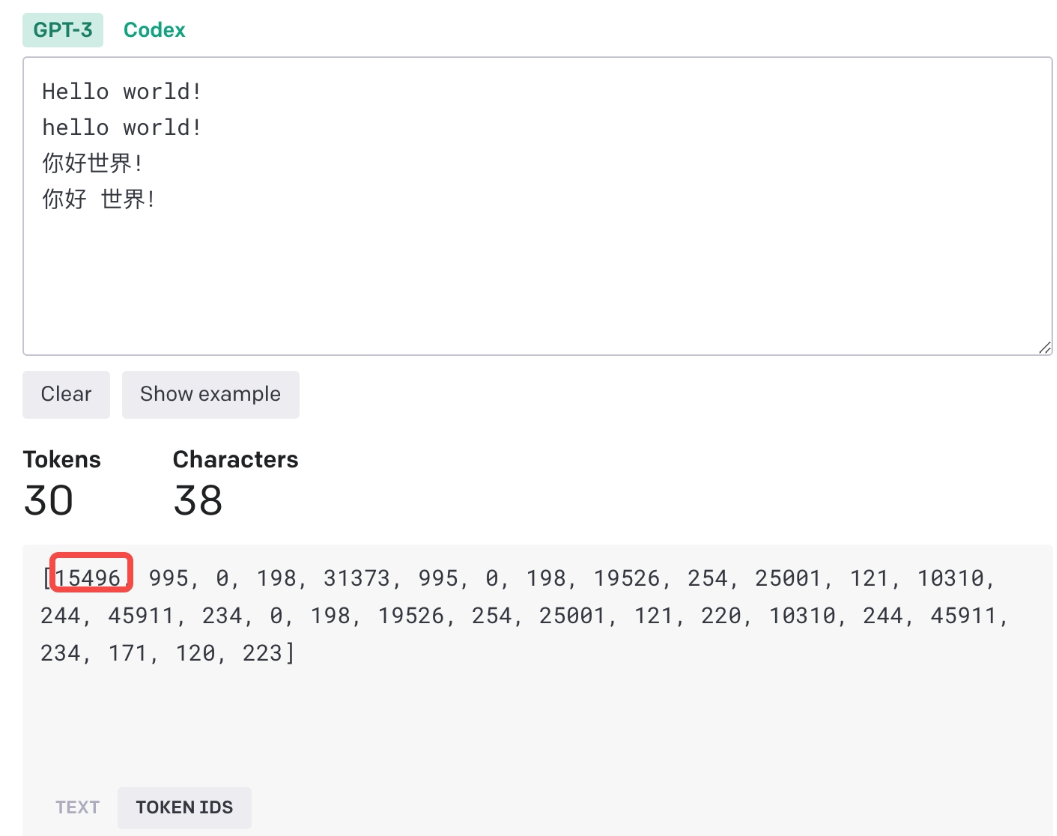
Tokenizer 诸如GPT3/4以及LlaMA/LlaMA2大语言模型都采用了token的作为模型的输入输出，其输入是文本，然后将文本转为token（正整数），然后从一串token（对应于文本）预测下一个token。 进入OpenAI官网提供的tokenizer可以看到GPT3tokenizer采用的方法。这里以Hello World为例说明。 总共30个token，英文单词一般会用单独的token表示，大小写也会区分不同的token，如Hello和hello，另外有一些由空格前导的单词也会单独编码，这会使得编码整个句子效率更高（这将省去每个空格的编码），对于中文token化，会使用两到三个ID（正整数表示），比如上面的中英文的！。 在英语等空白隔开的语言中，文本被预标记化，通常使用不跨...

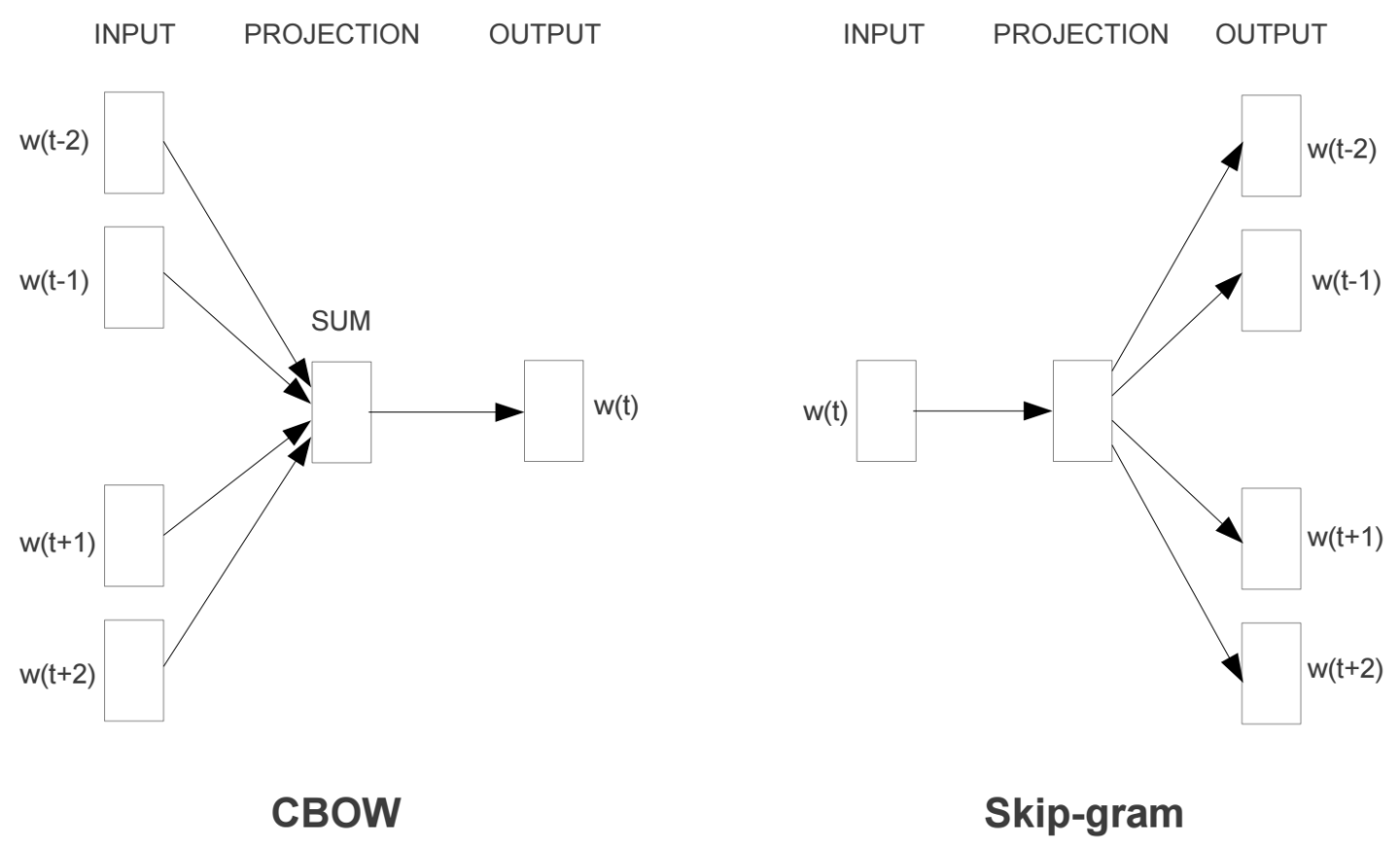
什么是Word2Vec和Embeddings？ Word2Vec是从大量文本语料中以无监督的方式学习语义知识的一种模型，它被大量地用在自然语言处理（NLP）中。那么它是如何帮助我们做自然语言处理呢？Word2Vec其实就是通过学习文本来用词向量的方式表征词的语义信息，即通过一个嵌入空间使得语义上相似的单词在该空间内距离很近。Embedding其实就是一个映射，将单词从原先所属的空间映射到新的多维空间中，也就是把原先词所在空间嵌入到一个新的空间中去。 我们从直观角度上来理解一下，cat这个单词和kitten属于语义上很相近的词，而dog和kitten则不是那么相近，iphone这个单词和kitten的语义就差的更远了。通过对词汇表中单词进行这种数值表示方式的学习（也就是将单词转换为词向量），能...

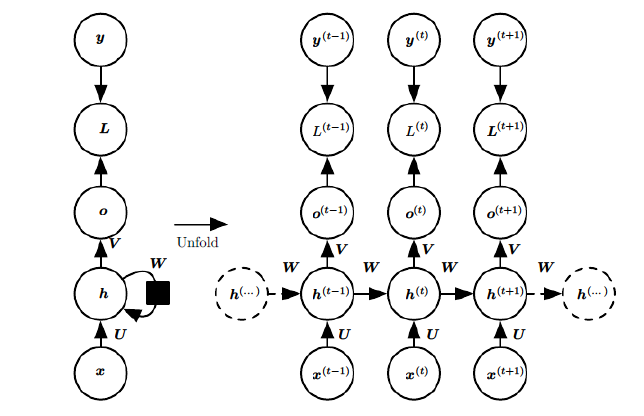
RNN 概述 在前面讲到的DNN和CNN中，训练样本的输入和输出是比较的确定的。但是有一类问题DNN和CNN不好解决，就是训练样本输入是连续的序列,且序列的长短不一，比如基于时间的序列：一段段连续的语音，一段段连续的手写文字。这些序列比较长，且长度不一，比较难直接的拆分成一个个独立的样本来通过DNN/CNN进行训练。 而对于这类问题，RNN则比较的擅长。那么RNN是怎么做到的呢？RNN假设我们的样本是基于序列的。比如是从序列索引1到序列索引 τ 。对于这其中的任意序列索引号 t ,它对应的输入是对应的样本序列中的 x(t) 。而模型在序列索引号 t 位置的隐藏状态 h(t) ，则由 x(t) 和在 t−1 位置的隐藏状态 h(t−1) 共同决定。在任意序列索引号 t ，我们也有对应的模型预测...

梯度检查点（Gradient Checkpointing） 大模型的参数量巨大，即使将batch_size设置为1并使用梯度累积的方式更新，也仍然会OOM。原因是通常在计算梯度时，我们需要将所有前向传播时的激活值保存下来，这消耗大量显存。 还有另外一种延迟计算的思路，丢掉前向传播时的激活值，在计算梯度时需要哪部分的激活值就重新计算哪部分的激活值，这样做倒是解决了显存不足的问题，但加大了计算量同时也拖慢了训练。 梯度检查点（Gradient Checkpointing）在上述两种方式之间取了一个平衡，这种方法采用了一种策略选择了计算图上的一部分激活值保存下来，其余部分丢弃，这样被丢弃的那一部分激活值需要在计算梯度时重新计算。 下面这个动图展示了一种简单策略：前向传播过程中计算节点的激活值并保存...

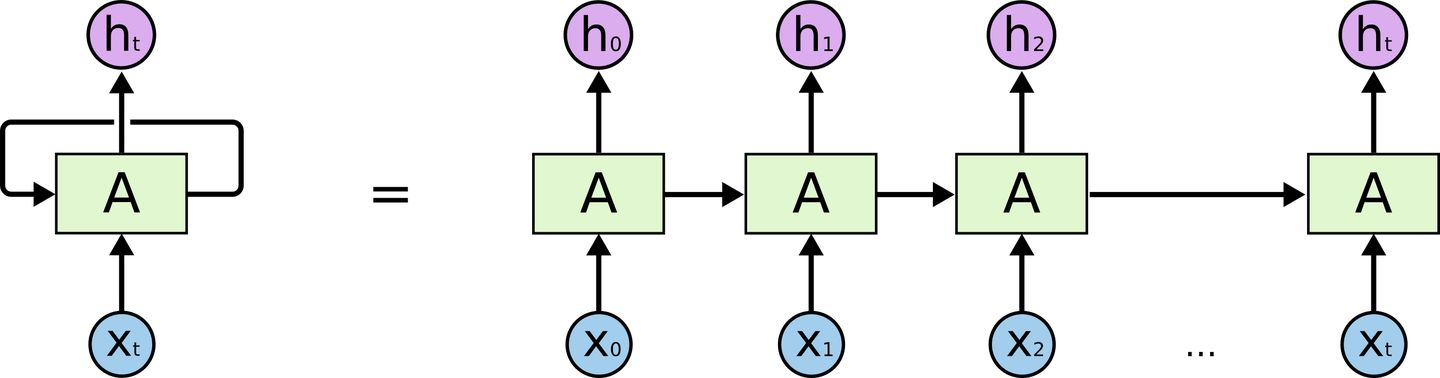
取代RNN——Transformer 在介绍Transformer前我们来回顾一下RNN的结构 对RNN有一定了解的话，一定会知道，RNN有两个很明显的问题 效率问题：需要逐个词进行处理，后一个词要等到前一个词的隐状态输出以后才能开始处理 如果传递距离过长还会有梯度消失、梯度爆炸和遗忘问题 为了缓解传递间的梯度和遗忘问题，设计了各种各样的RNN cell，最著名的两个就是LSTM和GRU了 LSTM (Long Short Term Memory) GRU (Gated Recurrent Unit) 但是，引用网上一个博主的比喻，这么做就像是在给马车换车轮，为什么不直接换成汽车呢？ 于是就有了Transformer。Transformer 是Google Brain 2017的提出的一篇工...

给定一个包含 n 维数据 x 的数据集 D , 简单起见，假设数据 [Math] . 由于真正对联合分布建模的时候， x，y 都是随机变量，故而只需讨论 p(X)=p(x_1,...,x_n) 即可，毕竟只需要令 x_n=y 即可。 给定一个具体的任务，如MNIST中的手写数字二值图分类，从Generative的角度进行Represent，并在Inference中Learning. 下面先介绍： 描述如何对这个MINST任务建模 p(X,Y) （Representation） 对MNIST任务建模 对于一张pixel为 [Math] 大小的图片，令 x_1 表示第一个pixel的随机变量， [Math] ，需明确： 任务目标：学习一个模型分布 [Math] ，使采样时 [Math] ， x ...

概述 SSM的概念由来已久，但这里我们特指深度学习中的SSM，一般认为其开篇之作是2021年的 S4，不算太老，而SSM最新最火的变体大概是Mamba。当然，当我们谈到SSM时，也可能泛指一切线性RNN模型，这样RWKV、RetNet还有此前LRU都可以归入此类。不少SSM变体致力于成为Transformer的竞争者，尽管笔者并不认为有完全替代的可能性，但SSM本身优雅的数学性质也值得学习一番。 尽管我们说SSM起源于S4，但在S4之前，SSM有一篇非常强大的奠基之作《HiPPO: Recurrent Memory with Optimal Polynomial Projections》（简称HiPPO），所以本文从HiPPO开始说起。 另外值得一提的是，SSM代表作HiPPO、S4、Mam...