INCOMING TRANSMISSION

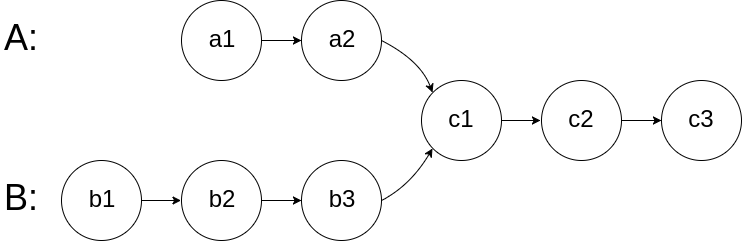
160. 相交链表 题目 给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。 图示两个链表在节点 c1 开始相交 ： 题目数据 保证 整个链式结构中不存在环。 注意 ，函数返回结果后，链表必须 保持其原始结构 。 自定义评测： 评测系统 的输入如下（你设计的程序 不适用 此输入）： intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0 listA - 第一个链表 listB - 第二个链表 skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数 skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数 评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。 示例 1： 输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2,...

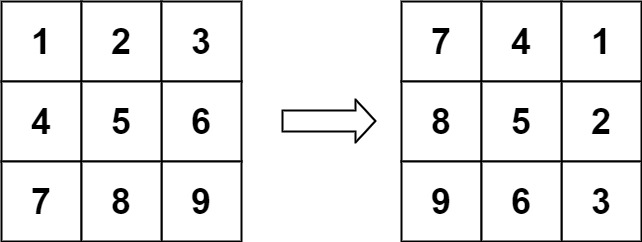
48. 旋转图像 题目 给定一个 \(n × n\) 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。 请不要 使用另一个矩阵来旋转图像。 示例 1： 输入：matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出：[[7,4,1],[8,5,2],[9,6,3]] 示例 2： 输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]] 提示： n == matrix.length == matrix[i].length 1 <= n <= 20 -1000 <= matrix[i][j] <= 1000 题解 这是一个经典的矩阵操作问题。要在原地（In-place）将图像顺时针旋转 90 度，我们可以利用矩阵的几何性质。 最直观且易于实现的方法是将...

数组&链表&字符串 双指针 滑动窗口 哈希表 哈希表 栈&队列 单调队列 树与堆 图 数学 Math

128. 最长连续序列 题目 给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 1： 输入：nums = [100,4,200,1,3,2] 输出：4 解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。 示例 2： 输入：nums = [0,3,7,2,5,8,4,6,0,1] 输出：9 示例 3： 输入：nums = [1,0,1,2] 输出：3 提示： 0 <= nums.length <= 10 5 -10 9 <= nums[i] <= 10 9 题解 我们需要在 \(O(1)\) 的时间内查找某个数是否存在。因此，首先将数组中的所有元素放入一个 HashSet 中。这不仅能去重，还能支持快速查找。 避免冗余计算 (关键优化) 如果我们对集合中的每一个数都尝试去向后计数（例如，对于 x ，尝试找 x+1 , x+2 ...），最坏情况下的时间复杂度会退化到 \(O(n^2)\) 。 优化策略 ： 我们 只从序列的起点开始计数 。...

76. 最小覆盖子串 题目 给定两个字符串 s 和 t ，长度分别是 m 和 n ，返回 s 中的 最短窗口 子串 ，使得该子串包含 t 中的每一个字符（ 包括重复字符 ）。如果没有这样的子串，返回空字符串 "" 。 测试用例保证答案唯一。 示例 1： 输入：s = "ADOBECODEBANC", t = "ABC" 输出："BANC" 解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。 示例 2： 输入：s = "a", t = "a" 输出："a" 解释：整个字符串 s 是最小覆盖子串。 示例 3: 输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中， 因此没有符合条件的子字符串，返回空字符串。 提示： m == s.length n == t.length 1 <= m, n <= 10 5 s 和 t 由英文字母组成 题解 这是一个经典的 滑动窗口 (Sliding Window) 问题 我们需要维护一个动态的窗口 [left, right] ： 右移扩大 ：不断移动...

简介 如果以概率的视角看待世界的生成模型。 在这样的世界观中，我们可以将任何类型的观察数据（例如 \(D\) ）视为来自底层分布（例如 \( p_{data}\) ）的有限样本集。 任何生成模型的目标都是在访问数据集 \(D\) 的情况下近似该数据分布。 如果我们能够学习到一个好的生成模型，我们可以将学习到的模型用于下游推理。 我们主要对数据分布的参数近似感兴趣，在一组有限的参数中，它总结了关于数据集 \(D\) 的所有信息。 与非参数模型相比，参数模型在处理大型数据集时能够更有效地扩展，但受限于可以表示的分布族。 在参数的设置中，我们可以将学习生成模型的任务视为在模型分布族中挑选参数，以最小化模型分布和数据分布之间的距离。 如上图，给定一个狗的图像数据集，我们的目标是学习模型族 \(M\) 中生成模型 θ 的参数，使得模型分布 \(p_θ\) 接近 \(p_{data}\) 上的数据分布。 在数学上，我们可以将我们的目标指定为以下优化问题: \[\mathop{min}\limits_{\theta\in M}d(p_\theta,p_{data})\] 其中， \(d()\)...

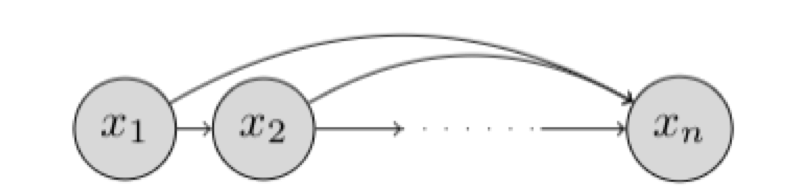
研究对象与基本设定 我们希望学习一个能够“生成数据”的概率模型。假设我们有一个数据集 \(D\) ，每个样本是 \(n\) 维二值向量： \(x \in \{0,1\}^n\) 我们的目标是用一个参数化分布 \(p_\theta(x)\) 去逼近真实数据分布 \(p_{\text{data}}(x)\) ，并最终能够： 密度估计 ：给定 \(x\) 计算 \(p_\theta(x)\) 或 \(\log p_\theta(x)\) 采样生成 ：从 \(p_\theta(x)\) 采样得到新的 \(x\) 表示：链式法则与自回归分解 链式法则分解联合分布 任意联合分布都可用概率链式法则分解为条件概率的乘积： \[p(x) = \prod_{i=1}^{n} p(x_i \mid x_1, x_2, \dots, x_{i-1}) = \prod_{i=1}^{n} p(x_i \mid x_{<i})\] 其中： \(x_{<i} = [x_1, x_2, \dots, x_{i-1}]\) ，这意味着：只要我们能为每个维度 \(i\) 学好一个条件分布 \(p(x_i \mid...

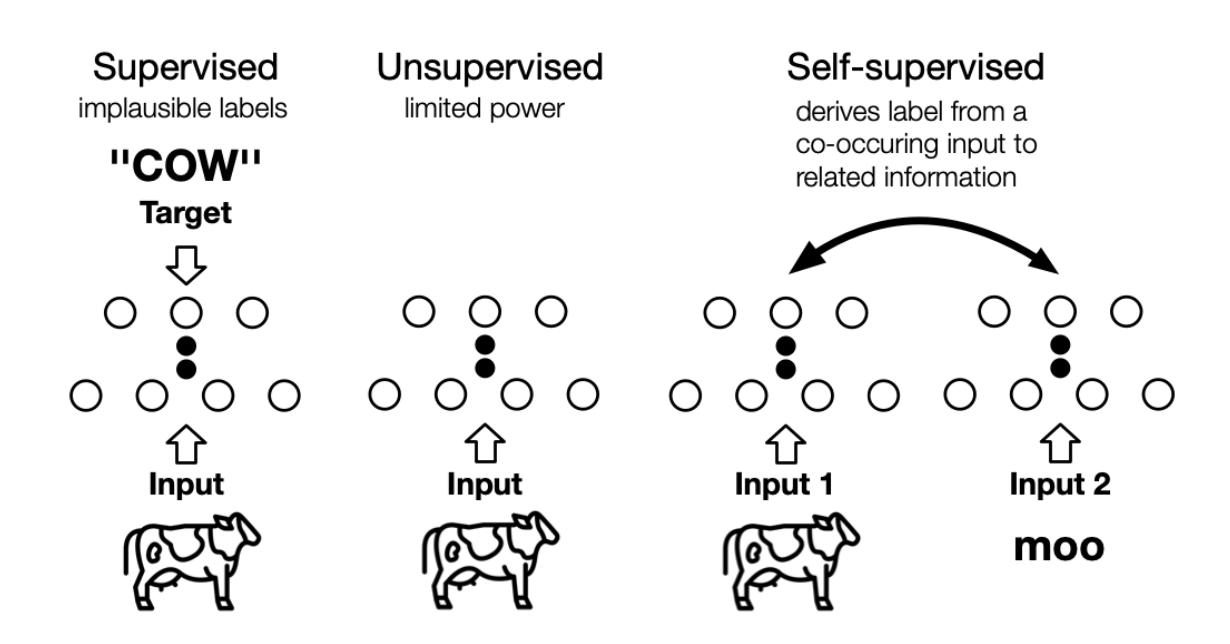
the machine predicts any parts of its input for any observed part 这是LeCun在AAAI 2020上对自监督学习的定义，再结合传统的自监督学习定义，可以总结如下两点特征： 通过“半自动”过程从数据本身获取“标签”； 从“其他部分”预测部分数据。 个人理解， 其实任意挖掘对象之间联系、探索不同对象共同本质的方法，都或多或少算是自监督学习的思想 。 自监督学习与无监督学习的区别主要在于，无监督学习专注于检测特定的数据模式，如聚类、社区发现或异常检测，而自监督学习的目标是恢复（recovering），仍处于监督学习的范式中。上图展示了三者之间的区别， 自监督中的“related information” 可以来自其他模态、输入的其他部分以及输入的不同形式。 Self-Supervised...

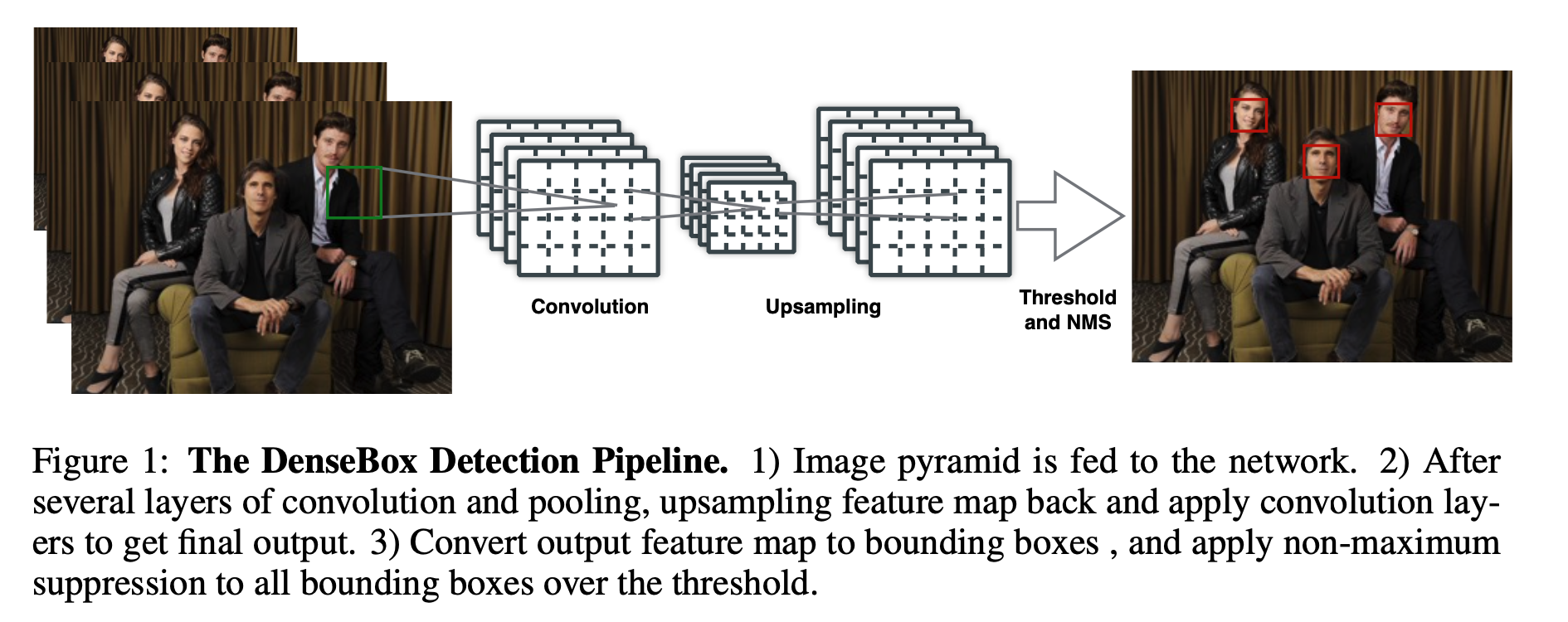
在正式介绍之前，先简单回顾一下现有的两大类方法。第一大类，也是从非Deep时代，乃至CV初期就被就被广泛使用的方法叫做image pyramid。在image pyramid中，我们直接对图像进行不同尺度的缩放，然后将这些图像直接输入到detector中去进行检测。虽然这样的方法十分简单，但其效果仍然是最佳，也后续启发了SNIP这一系列的工作。单论性能而言，multiscale training/testing仍然是一个不可缺少的组件。然而其缺点也是很明显的，测试时间大幅度提高，对于实际使用并不友好。 另外一大类方法，也是Deep方法所独有的，也就是feature pyramid。最具代表性的工作便是经典的FPN了。这一类方法的思想是直接在feature层面上来近似image pyramid...

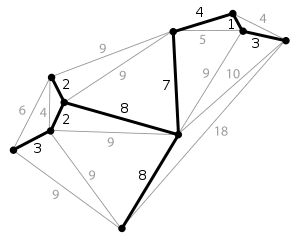
简介 生成树（spanning tree） 在图论中，无向图 G=(V,E) 的生成树（spanning tree)是具有G的全部顶点，但边数最少的联通子图。假设G中一共有n个顶点，一颗生成树满足下列条件： （1）n个顶点； （2）n1条边； （3）n个顶点联通； （4）一个图的生成树可能有多个。最小生成树（minimum spanning tree， MST）/最小生成森林：联通加权无向图中边缘权重加和最小的生成树。给定无向图 G=(V,E) ， (u,v) 代表顶点 u 与顶点 v 的边， w(u,v) 代表此边的权重，若存在生成树T使得： [公式] 最小，则 T 为 G 的最小生成树。对于非连通无向图来说，它的每一连通分量同样有最小生成树，它们的并被称为最小生成森林。最小生成树除了继承...

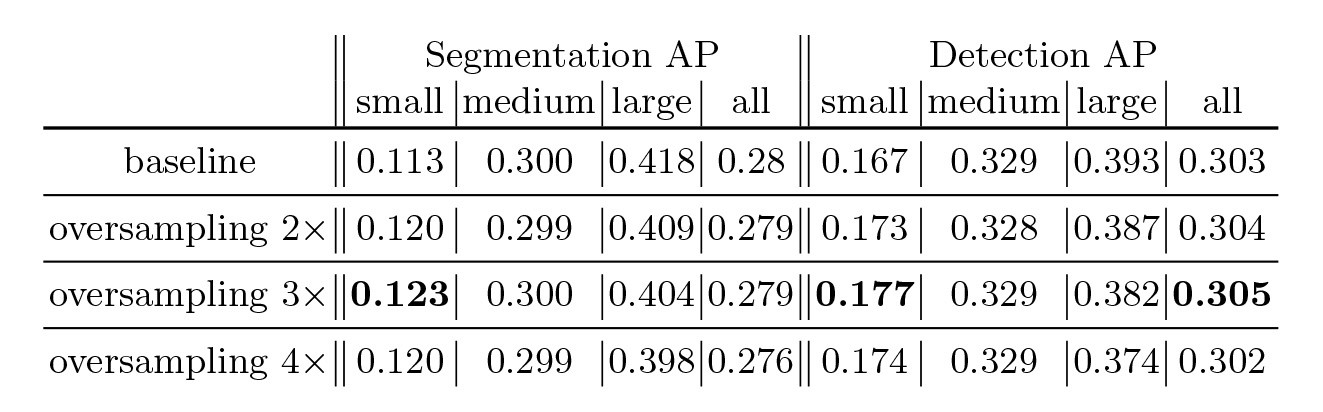
在深度学习目标检测中，特别是人脸检测中，由于分辨率低、图像模糊、信息少、噪声多，小目标和小人脸的检测一直是一个实用和常见的难点问题。然而，在过去几年的发展中，也出现了一些提高小目标检测性能的解决方案。本文将对这些方法进行分析、整理和总结。 图像金字塔和多尺度滑动窗口检测 一开始，在深学习方法成为流行之前，对于不同尺度的目标，通常是从原始图像开始，使用不同的分辨率构建图像金字塔，然后使用分类器对金字塔的每一层进行滑动窗口的目标检测。 在著名的人脸检测器MTCNN中，使用图像金字塔法检测不同分辨率的人脸目标。然而，这种方法通常是缓慢的，虽然构建图像金字塔可以使用卷积核分离加速或简单粗暴地缩放，但仍需要做多个特征提取，后来有人借其想法想出一个特征金字塔网络FPN，在不同层融合特征，只需要一次正向计...

简介 "Anchorfree"（无锚点）是一种目标检测方法，与传统的使用锚框（anchor boxes）的方法（例如Faster RCNN）不同。在传统方法中，锚框是预先定义的、具有不同尺寸和长宽比的矩形区域，用于捕捉不同尺寸和形状的目标。而在"anchorfree"方法中，不再使用锚框，而是直接预测目标的位置和形状，通常使用网络输出的热图和偏移信息。 以下是对"anchorfree"方法的一些关键理解点： 无需预定义锚框： 在传统目标检测方法中，需要事先定义和生成一组锚框，这可能需要大量的人工工作。而在"anchorfree"方法中，不再需要锚框，模型可以自动学习目标的位置和形状。 直接位置和形状回归： "anchorfree"方法通过输出的热图来表示目标的存在概率，并使用偏移信息来定位目...