INCOMING TRANSMISSION

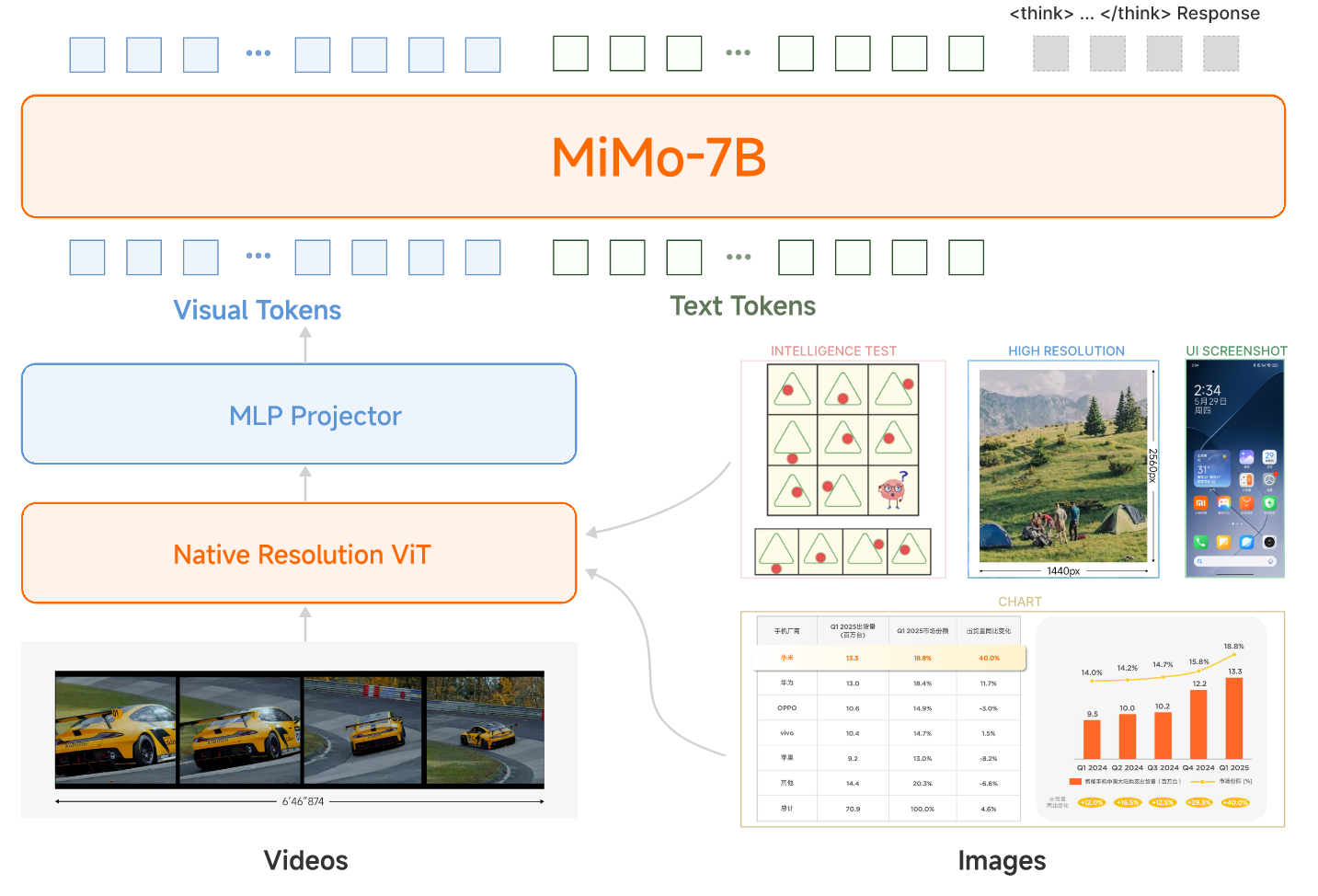
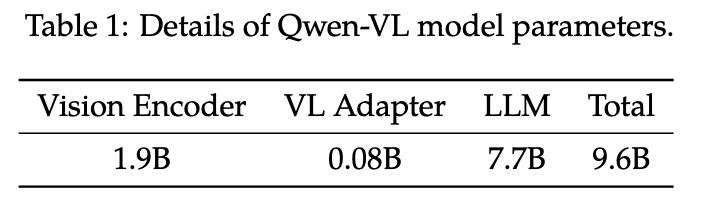
概述 小米团队近日发布了MIMO-VL-7B-SFT和MIMO-VL-7B-RL，这是两个强大的视觉语言模型，MIMO-VL-7B-RL在40个评估任务中的35个上优于QWEN2.5-VL-7B，对于GUI Grounding任务，它在OSWorld-G上设置了一个新标准，甚至超过了UI-TARS等专业模型。模型通过四个阶段的预训练（2.4T Token）与Mixed On-policy 强化（MORL）整合了多样化的奖励信号。 在文章中，作者提到了两个重要的发现： 从Pre-Traing 训练阶段中加入高质量且覆盖广的推理数据对于强化模型性能至关重要。 Mixed On-policy 强化学习进一步增强了模型的性能，同时实现了稳定的同时改进仍然在性能方面具有挑战性。 Pre-Training 模型结构 整个模型还是采用了VIT-MLP-LLM的结构，具体来说，视觉模型采用了Qwen2.5-VL中的视觉encoder，LLM采用了自家的语言模型MiMo-7B-Base。 整个Pretraining采用了四个阶段的训练，每个阶段采用的数据，模型训练参数和模型参数如下面两表所示...

MiniCPM-V系列是面壁智能推出的小参数量的开源多模态大模型，没有超过9B的版本。主打小而强。 MiniCPM-Llama3-V 2.5 这版有论文了，详细写。应该也是2.6的基础。 这一版在 OpenCompass 评估中优于强大的 GPT-4V-1106、Gemini Pro 和 Claude 3。 能力 支持最高1.8M像素的高分辨率图像输入（例如1344*1344），支持任意长宽比图像 强大的OCR，OCRBench 上优于 GPT-4V、Gemini Pro 和 Qwen-VL-Max，支持table-to-markdown 可信，基于RLAIF-V技术做了对齐，减少幻觉，更符合人类喜好 多语言，基于VisCPM技术，支持30多种语言 系统地集成了一套端侧部署优化技术 模型架构 基本架构 三部分：visual encoder, 压缩层, LLM visual encoder：SigLIP SoViT-400m/14 压缩层：单层交叉注意力 LLM：每一代都不同 Adaptive Visual Encoding...

InternVL Blog： https://internvl.github.io/blog/ Github： https://github.com/OpenGVLab/InternVL InternVL 1.0 对齐策略 语言模型和视觉模型各自发展，各有突破，但如何让语言模型会看图，或者让视觉模型会说话？为了将视觉模型与语言模型进行连接，对齐如同“胶水”,将两种模型链接在一起，如使用QFormer或线性投影这样的轻量级“胶水”层，来形成视觉-语言模型，如InstructBLIP和LLaVA，但均存在局限性。 现有对齐策略的局限性 参数规模的不一致： LLM的参数规模已经达到1000亿，而广泛使用的VLLM的视觉编码器仍在10亿参数左右。这种差距可能导致LLM的能力无法被充分利用。 特征表示的不一致： 在纯视觉数据上训练的视觉模型或与BERT系列对齐的模型往往与LLM存在表示上的不一致。 连接效率低下： “胶水”层通常是轻量的、随机初始化的，可能无法捕捉到多模态理解和生成所需的丰富的跨模态交互和依赖关系。 InternVL引入全新的对齐策略...

Qwen-VL 模型框架 Qwen-VL的整体网络架构由三个组件组成： LLM：使用 Qwen-7B 的预训练权重进行初始化。 视觉编码器：Qwen-VL 的可视化编码器使用ViT 架构，使用 Openclip 的 ViT-bigG 的预训练权重进行初始化。在训练和推理过程中，输入图像的大小都会调整为特定分辨率。视觉编码器通过以 14 步幅将图像分割成块来处理图像，生成一组图像特征。 位置感知视觉语言适配器：为了缓解长图像特征序列带来的效率问题，Qwen-VL 引入了一种视觉语言适配器来压缩图像特征。类似QFormer，该适配器包括一个随机初始化的单层交叉注意力模块。使用一组可训练向量（嵌入）作为query，并将视觉编码器中的图像特征作为交叉注意力作的key。该机制将视觉特征序列压缩到固定长度 256。 图像输入 图像不会直接以像素形式喂给语言模型（LLM）。 典型流程是： Visual Encoder ：把图片编码成一串视觉特征（embedding/feature sequence）。 Adapter ：把视觉特征映射到语言模型可接入的表征空间/维度。 最终得到：...

128. 最长连续序列 题目 给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 1： 输入：nums = [100,4,200,1,3,2] 输出：4 解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。 示例 2： 输入：nums = [0,3,7,2,5,8,4,6,0,1] 输出：9 示例 3： 输入：nums = [1,0,1,2] 输出：3 提示： 0 <= nums.length <= 10 5 -10 9 <= nums[i] <= 10 9 题解 我们需要在 \(O(1)\) 的时间内查找某个数是否存在。因此，首先将数组中的所有元素放入一个 HashSet 中。这不仅能去重，还能支持快速查找。 避免冗余计算 (关键优化) 如果我们对集合中的每一个数都尝试去向后计数（例如，对于 x ，尝试找 x+1 , x+2 ...），最坏情况下的时间复杂度会退化到 \(O(n^2)\) 。 优化策略 ： 我们 只从序列的起点开始计数 。...

76. 最小覆盖子串 题目 给定两个字符串 s 和 t ，长度分别是 m 和 n ，返回 s 中的 最短窗口 子串 ，使得该子串包含 t 中的每一个字符（ 包括重复字符 ）。如果没有这样的子串，返回空字符串 "" 。 测试用例保证答案唯一。 示例 1： 输入：s = "ADOBECODEBANC", t = "ABC" 输出："BANC" 解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。 示例 2： 输入：s = "a", t = "a" 输出："a" 解释：整个字符串 s 是最小覆盖子串。 示例 3: 输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中， 因此没有符合条件的子字符串，返回空字符串。 提示： m == s.length n == t.length 1 <= m, n <= 10 5 s 和 t 由英文字母组成 题解 这是一个经典的 滑动窗口 (Sliding Window) 问题 我们需要维护一个动态的窗口 [left, right] ： 右移扩大 ：不断移动...

💡 扩散模型：通过加噪的方式去学习原始数据的分布， 从学到的分布中去生成样本 DDPM 关键点： 1. 正向加噪是离散时间马尔可夫链：从 \(x_0\) 逐步加噪得到 \(x_1,x_2,...,x_T\) ；在合适的噪声调度与足够大的 \(T\) 下， \(x_T\) 近似服从 \( N(0,I) \) 的各向同性高斯。 2. 每一步噪声方差 \(β_t\) 满足 \(0<β_t<1\) ，通常随 \(t\) 增大；因此 \(q(x_t|x_{t-1}) \) 的均值缩放系数 \(\sqrt{1-β_t} \) 逐渐减小。 3. 训练通过最大化对数似然的变分下界（ELBO）来学习反向过程 \( p_θ(x_{t-1}|x_t)\) ，并将其参数化为高斯分布（神经网络预测均值/噪声或 score）。 4. 将目标写成 score/DSM 形式时，loss 的权重与对应噪声层的方差尺度（如 \(1-\bar{α}_t\) 或相关量）有关；采样通常是按学习到的反向转移逐步生成（祖先采样），与经典 Langevin MCMC 更新形式不同，但可在 SDE 视角下统一理解。...

基于文章 《Elucidating the Design Space of Diffusion-Based Generative Models》 来统一扩散模型框架 通用扩散模型框架推导 加噪公式 Flow Matching的一步加噪公式 \[\mathbf{x}_t=(1-t)\mathbf{x}_0+t\varepsilon\] 写成概率分布形式： \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;(1-t)\mathbf{x}_0,t^2\mathbf{I})\] Score Matching的一步加噪公式 \[\mathbf{x}_t=\mathbf{x}_0+\sigma_t\varepsilon \] 写成概率分布形式： \[p(\mathbf{x}_t|\mathbf{x}_0)=\mathcal{N}(\mathbf{x}_t;\mathbf{x}_0,\sigma_t^2\mathbf{I})\] DDPM/DDIM的一步加噪公式...

简介 如果以概率的视角看待世界的生成模型。 在这样的世界观中，我们可以将任何类型的观察数据（例如 \(D\) ）视为来自底层分布（例如 \( p_{data}\) ）的有限样本集。 任何生成模型的目标都是在访问数据集 \(D\) 的情况下近似该数据分布。 如果我们能够学习到一个好的生成模型，我们可以将学习到的模型用于下游推理。 我们主要对数据分布的参数近似感兴趣，在一组有限的参数中，它总结了关于数据集 \(D\) 的所有信息。 与非参数模型相比，参数模型在处理大型数据集时能够更有效地扩展，但受限于可以表示的分布族。 在参数的设置中，我们可以将学习生成模型的任务视为在模型分布族中挑选参数，以最小化模型分布和数据分布之间的距离。 如上图，给定一个狗的图像数据集，我们的目标是学习模型族 \(M\) 中生成模型 θ 的参数，使得模型分布 \(p_θ\) 接近 \(p_{data}\) 上的数据分布。 在数学上，我们可以将我们的目标指定为以下优化问题: \[\mathop{min}\limits_{\theta\in M}d(p_\theta,p_{data})\] 其中， \(d()\)...

2022年中旬，以扩散模型为核心的图像生成模型将AI绘画带入了大众的视野。实际上，在更早的一年之前，就有了一个能根据文字生成高清图片的模型——VQGAN。VQGAN不仅本身具有强大的图像生成能力，更是传承了前作VQVAE把图像压缩成离散编码的思想，推广了「先压缩，再生成」的两阶段图像生成思路，启发了无数后续工作。 VQGAN 核心思想 VQGAN的论文名为 Taming Transformers for High-Resolution Image Synthesis，直译过来是「驯服Transformer模型以实现高清图像合成」。可以看出，该方法是在用Transformer生成图像。可是，为什么这个模型叫做VQGAN，是一个GAN呢？这是因为，VQGAN使用了两阶段的图像生成方法： 训练时，先训练一个图像压缩模型（包括编码器和解码器两个子模型），再训练一个生成压缩图像的模型。 生成时， 先用第二个模型生成出一个压缩图像，再用第一个模型复原成真实图像 。 其中，第一个图像压缩模型叫做VQGAN，第二个压缩图像生成模型是一个基于Transformer的模型。...

本文受启发于著名的国外博文 《Wasserstein GAN and the Kantorovich-Rubinstein Duality》 ，内容跟它大体上相同，但是删除了一些冗余的部分，对不够充分或者含糊不清的地方作了补充。 Wasserstein距离 显然，整篇文章必然围绕着Wasserstein距离（ \(\mathcal{W}\) 距离）来展开。假设我们有了两个概率分布 \(p(x),q(x)\) ，那么Wasserstein距离的定义为 \[\mathcal{W}[p,q]=\inf_{\gamma\in \Pi[p,q]} \iint \gamma(\boldsymbol{x},\boldsymbol{y}) d(\boldsymbol{x},\boldsymbol{y}) d\boldsymbol{x}d\boldsymbol{y}\] 事实上，这也算是最优传输理论中最核心的定义了。 成本函数 首先 \(d(x,y)\) ，它不一定是距离，其准确含义应该是一个成本函数，代表着从 \(x\) 运输到 \(y\) 的成本。常用的 \(d\) 是基于 \(l\)...

简介 生成对抗网络 ( Generative Adversarial Network, GAN ) 是由 Goodfellow 于 2014 年提出的一种对抗网络。这个网络框架包含两个部分，一个生成模型 (generative model) 和一个判别模型 (discriminative model)。其中，生成模型可以理解为一个伪造者，试图通过构造假的数据骗过判别模型的甄别；判别模型可以理解为一个警察，尽可能甄别数据是来自于真实样本还是伪造者构造的假数据。两个模型都通过不断的学习提高自己的能力，即生成模型希望生成更真的假数据骗过判别模型，而判别模型希望能学习如何更准确的识别生成模型的假数据。 网络框架 GAN 由两部分构成，一个 生成器 ( Generator ) 和一个 判别器 ( Discriminator )。对于生成器，我们需要学习关于数据 \(x\) 的一个分布 \(p_g\) ，首先定义一个输入数据的先验分布 \(p_z(z)\) ，其次定义一个映射 \(G \left(\boldsymbol{z}; \theta_g\right): \boldsymbol{z}...