INCOMING TRANSMISSION

129. 滑动窗口最大值 题目 给你一个整数数组 nums ，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 示例 1： 输入：nums = [1,3,-1,-3,5,3,6,7], k = 3 输出：[3,3,5,5,6,7] 解释： 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7 示例 2： 输入：nums = [1], k = 1 输出：[1] 提示： 1 <= nums.length...

简介 如果以概率的视角看待世界的生成模型。 在这样的世界观中，我们可以将任何类型的观察数据（例如 \(D\) ）视为来自底层分布（例如 \( p_{data}\) ）的有限样本集。 任何生成模型的目标都是在访问数据集 \(D\) 的情况下近似该数据分布。 如果我们能够学习到一个好的生成模型，我们可以将学习到的模型用于下游推理。 我们主要对数据分布的参数近似感兴趣，在一组有限的参数中，它总结了关于数据集 \(D\) 的所有信息。 与非参数模型相比，参数模型在处理大型数据集时能够更有效地扩展，但受限于可以表示的分布族。 在参数的设置中，我们可以将学习生成模型的任务视为在模型分布族中挑选参数，以最小化模型分布和数据分布之间的距离。 如上图，给定一个狗的图像数据集，我们的目标是学习模型族 \(M\) 中生成模型 θ 的参数，使得模型分布 \(p_θ\) 接近 \(p_{data}\) 上的数据分布。 在数学上，我们可以将我们的目标指定为以下优化问题: \[\mathop{min}\limits_{\theta\in M}d(p_\theta,p_{data})\] 其中， \(d()\)...

2022年中旬，以扩散模型为核心的图像生成模型将AI绘画带入了大众的视野。实际上，在更早的一年之前，就有了一个能根据文字生成高清图片的模型——VQGAN。VQGAN不仅本身具有强大的图像生成能力，更是传承了前作VQVAE把图像压缩成离散编码的思想，推广了「先压缩，再生成」的两阶段图像生成思路，启发了无数后续工作。 VQGAN 核心思想 VQGAN的论文名为 Taming Transformers for High-Resolution Image Synthesis，直译过来是「驯服Transformer模型以实现高清图像合成」。可以看出，该方法是在用Transformer生成图像。可是，为什么这个模型叫做VQGAN，是一个GAN呢？这是因为，VQGAN使用了两阶段的图像生成方法： 训练时，先训练一个图像压缩模型（包括编码器和解码器两个子模型），再训练一个生成压缩图像的模型。 生成时， 先用第二个模型生成出一个压缩图像，再用第一个模型复原成真实图像 。 其中，第一个图像压缩模型叫做VQGAN，第二个压缩图像生成模型是一个基于Transformer的模型。...

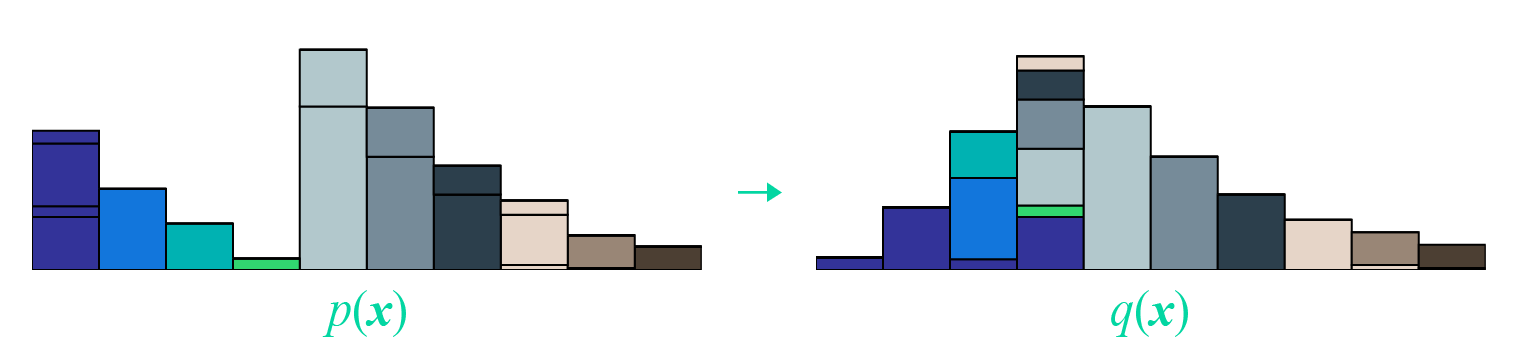
本文受启发于著名的国外博文 《Wasserstein GAN and the Kantorovich-Rubinstein Duality》 ，内容跟它大体上相同，但是删除了一些冗余的部分，对不够充分或者含糊不清的地方作了补充。 Wasserstein距离 显然，整篇文章必然围绕着Wasserstein距离（ \(\mathcal{W}\) 距离）来展开。假设我们有了两个概率分布 \(p(x),q(x)\) ，那么Wasserstein距离的定义为 \[\mathcal{W}[p,q]=\inf_{\gamma\in \Pi[p,q]} \iint \gamma(\boldsymbol{x},\boldsymbol{y}) d(\boldsymbol{x},\boldsymbol{y}) d\boldsymbol{x}d\boldsymbol{y}\] 事实上，这也算是最优传输理论中最核心的定义了。 成本函数 首先 \(d(x,y)\) ，它不一定是距离，其准确含义应该是一个成本函数，代表着从 \(x\) 运输到 \(y\) 的成本。常用的 \(d\) 是基于 \(l\)...

简介 生成对抗网络 ( Generative Adversarial Network, GAN ) 是由 Goodfellow 于 2014 年提出的一种对抗网络。这个网络框架包含两个部分，一个生成模型 (generative model) 和一个判别模型 (discriminative model)。其中，生成模型可以理解为一个伪造者，试图通过构造假的数据骗过判别模型的甄别；判别模型可以理解为一个警察，尽可能甄别数据是来自于真实样本还是伪造者构造的假数据。两个模型都通过不断的学习提高自己的能力，即生成模型希望生成更真的假数据骗过判别模型，而判别模型希望能学习如何更准确的识别生成模型的假数据。 网络框架 GAN 由两部分构成，一个 生成器 ( Generator ) 和一个 判别器 ( Discriminator )。对于生成器，我们需要学习关于数据 \(x\) 的一个分布 \(p_g\) ，首先定义一个输入数据的先验分布 \(p_z(z)\) ，其次定义一个映射 \(G \left(\boldsymbol{z}; \theta_g\right): \boldsymbol{z}...

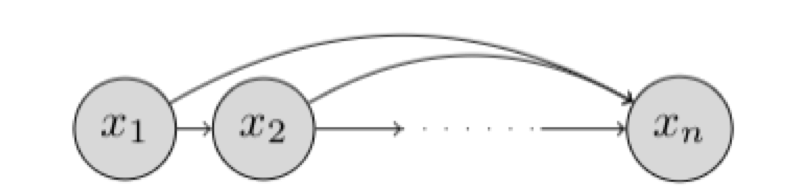
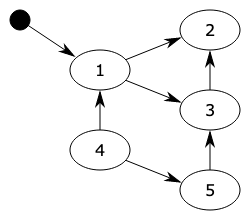
研究对象与基本设定 我们希望学习一个能够“生成数据”的概率模型。假设我们有一个数据集 \(D\) ，每个样本是 \(n\) 维二值向量： \(x \in \{0,1\}^n\) 我们的目标是用一个参数化分布 \(p_\theta(x)\) 去逼近真实数据分布 \(p_{\text{data}}(x)\) ，并最终能够： 密度估计 ：给定 \(x\) 计算 \(p_\theta(x)\) 或 \(\log p_\theta(x)\) 采样生成 ：从 \(p_\theta(x)\) 采样得到新的 \(x\) 表示：链式法则与自回归分解 链式法则分解联合分布 任意联合分布都可用概率链式法则分解为条件概率的乘积： \[p(x) = \prod_{i=1}^{n} p(x_i \mid x_1, x_2, \dots, x_{i-1}) = \prod_{i=1}^{n} p(x_i \mid x_{<i})\] 其中： \(x_{<i} = [x_1, x_2, \dots, x_{i-1}]\) ，这意味着：只要我们能为每个维度 \(i\) 学好一个条件分布 \(p(x_i \mid...

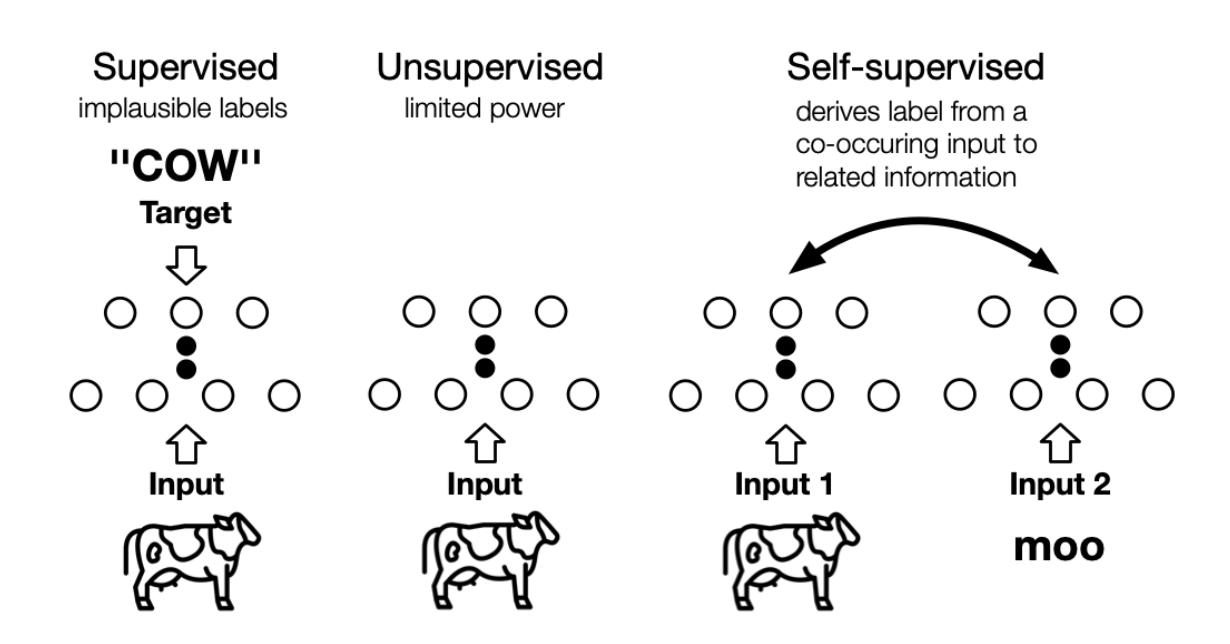
the machine predicts any parts of its input for any observed part 这是LeCun在AAAI 2020上对自监督学习的定义，再结合传统的自监督学习定义，可以总结如下两点特征： 通过“半自动”过程从数据本身获取“标签”； 从“其他部分”预测部分数据。 个人理解， 其实任意挖掘对象之间联系、探索不同对象共同本质的方法，都或多或少算是自监督学习的思想 。 自监督学习与无监督学习的区别主要在于，无监督学习专注于检测特定的数据模式，如聚类、社区发现或异常检测，而自监督学习的目标是恢复（recovering），仍处于监督学习的范式中。上图展示了三者之间的区别， 自监督中的“related information” 可以来自其他模态、输入的其他部分以及输入的不同形式。 Self-Supervised...

1. 列表和元组总结 列表和元组都是一个可以放置任意数据类型的有序集合，他们有以下共同点 列表和元组中的元素可以任意，并且都可以嵌套。 列表和元组都支持索引，且都支持负数索引，1表示最后一个元素，2表示倒数第二个元素 列表和元组都支持切片操作 都支持in关键词 都可以使用.index()、.count()、sorted()和enumerate()等方法 两者之间的相互转换，list()和tuple() 但是他们也是有区别 列表是动态的，长度大小不固定，可以随意地增加、删减或者改变元素（mutable） 元组是静态的，长度大小不固定，无法增删改，想要对已有的元组做任何“改变”，就只能开辟一块内存，创建新的元组 2. 列表和元组存储方式的差异 由于列表是动态的；元组是静态的，不可变的。这样的差异...

生成器 什么是生成器？ 通过列表生成式，我们可以直接创建一个列表，但是，受到内存限制，列表容量肯定是有限的，而且创建一个包含100万个元素的列表，不仅占用很大的存储空间，如果我们仅仅需要访问前面几个元素，那后面绝大多数元素占用的空间都白白浪费了。 所以，如果列表元素可以按照某种算法推算出来，那我们是否可以在循环的过程中不断推算出后续的元素呢？这样就不必创建完整的list，从而节省大量的空间，在Python中，这种一边循环一边计算的机制，称为生成器：generator 生成器是一个特殊的程序，可以被用作控制循环的迭代行为，python中生成器是迭代器的一种，使用yield返回值函数，每次调用yield会暂停，而可以使用next()函数和send()函数恢复生成器。 生成器类似于返回值为数组的一...

概念 可变对象与不可变对象的区别在于对象本身是否可变。 python内置的一些类型中 可变对象：list dict set 不可变对象：tuple string int float bool 举一个例子 [代码] 上面例子很直观地展现了，可变对象是可以直接被改变的，而不可变对象则不可以 地址问题 下面我们来看一下可变对象的内存地址变化 [代码] 我们可以看到，可变对象变化后，地址是没有改变的 如果两个变量同时指向一个地址 1.可变对象 [代码] 我们可以看到，改变a则b也跟着变，因为他们始终指向同一个地址 2.不可变对象 [代码] 我们可以看到，a改变后，它的地址也发生了变化，而b则维持原来的地址，原来地址中的内容也没有发生变化 作为函数参数 1.可变对象 [代码] 我们可以看到，可变对象作...

概述 python采用的是引用计数机制为主，标记清除和分代收集两种机制为辅的策略。 引用计数 Python语言默认采用的垃圾收集机制是『引用计数法 Reference Counting』，该算法最早George E. Collins在1960的时候首次提出，50年后的今天，该算法依然被很多编程语言使用。 『引用计数法』的原理是：每个对象维护一个ob_ref字段，用来记录该对象当前被引用的次数，每当新的引用指向该对象时，它的引用计数ob_ref加1，每当该对象的引用失效时计数ob_ref减1，一旦对象的引用计数为0，该对象立即被回收，对象占用的内存空间将被释放。 它的缺点是需要额外的空间维护引用计数，这个问题是其次的，不过最主要的问题是它不能解决对象的“循环引用”，因此，也有很多语言比如Jav...

Pycharm 的图形化界面虽然好用，但是在某些场景中，是无法使用的。而 Python 本身已经给我们提供了一个调试神器 pdb. 准备文件 在调试之前先将这两个文件准备好（做为演示用），并放在同级目录中。 utils.py [代码] pdb_demo.py [代码] 进入调试模式 主要有两种方法 做为脚本调用，方法很简单，就像正常执行python脚本一样，只是多加了m pdb [代码] 使用这个方式进入调试模式，会在脚本的第一行开始单步调试。 对于单文件的脚本并没有什么问题，如果是一个大型的项目，项目里有很多的文件，使用这种方式只能大大降低我们的效率。 一般情况下，都会直接在你需要的地方打一个断点，那如何打呢？ 只需在你想要打断点的地方加上这两行。 [代码] 然后执行时，也不需要再指定m ...